Home >Java >javaTutorial >Java Bellman-Ford algorithm principle and implementation method
Java Bellman-Ford algorithm principle and implementation method
- 王林forward
- 2023-05-18 23:58:381674browse
One point
If you encounter a negative weight edge, when there is no negative loop (the sum of the weights of the loop is negative), the Bellman-Ford algorithm can be used to solve the shortest path. The advantage of this algorithm is that it can handle the case of negative variable weights and is simple to implement, but its disadvantage is that the time complexity is too high. But the algorithm can be optimized in several ways to increase efficiency.
The Bellman-Ford algorithm is similar to the Dijkstra algorithm, both based on relaxation operations. The Dijkstra algorithm uses a greedy method to select the unprocessed node with the smallest weight, and then relaxes it; while the Bellman-Ford algorithm relaxes all edges a total of n-1 times. If the nth operation can still relax, then there must be a negative loop, because the negative loop can continuously reduce the length of the shortest path. The number of nodes is n and the number of edges is m, then the maximum running time of the Bellman-Ford algorithm is O(nm).
2 Algorithm steps
1 Data structure
Because edges need to be used for relaxation, edge set array storage is used. Each edge has three domains: two endpoints a and b, and edge weight w
2 Relaxation operation
For all edges j(a,b,w), if dis[ e[j]b]>dis[e[j].a] e[j].w, then it is relaxed, and dis[e[j]b]=dis[e[j].a] e[j] .w. Among them, dis[v] represents the shortest path length from the source point to node v.
3 Repeat the relaxation operation n-1 times
4 Negative loop judgment
Perform the relaxation operation again. If it can still be relaxed, it means there is a right negative loop.
Three algorithm implementation
package graph.bellmanford;
import java.util.Scanner;
public class BellmanFord {
static node e[] = new node[210];
static int dis[] = new int[110];
static int n;
static int m;
static int cnt = 0;
static {
for (int i = 0; i < e.length; i++) {
e[i] = new node();
}
}
static void add(int a, int b, int w) {
e[cnt].a = a;
e[cnt].b = b;
e[cnt++].w = w;
}
static boolean bellman_ford(int u) { // 求源点 u 到其它顶点的最短路径长度,判负环
for (int i = 0; i < dis.length; i++) {
dis[i] = 0x3f;
}
dis[u] = 0;
for (int i = 1; i < n; i++) { // 执行 n-1 次
boolean flag = false;
for (int j = 0; j < m; j++) // 边数 m 或 cnt
if (dis[e[j].b] > dis[e[j].a] + e[j].w) {
dis[e[j].b] = dis[e[j].a] + e[j].w;
flag = true;
}
if (!flag)
return false;
}
for (int j = 0; j < m; j++) // 再执行 1 次,还能松弛说明有环
if (dis[e[j].b] > dis[e[j].a] + e[j].w)
return true;
return false;
}
static void print() { // 输出源点到其它节点的最短距离
System.out.println("最短距离:");
for (int i = 1; i <= n; i++)
System.out.print(dis[i] + " ");
System.out.println();
}
public static void main(String[] args) {
int a, b, w;
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
for (int i = 0; i < m; i++) {
a = scanner.nextInt();
b = scanner.nextInt();
w = scanner.nextInt();
add(a, b, w);
}
if (bellman_ford(1)) // 判断负环
System.out.println("有负环!");
else
print();
}
}
class node {
int a;
int b;
int w;
}Four tests
1 Test without negative loop
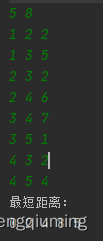
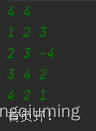
2 Test with negative loop test
The above is the detailed content of Java Bellman-Ford algorithm principle and implementation method. For more information, please follow other related articles on the PHP Chinese website!

