This article will help you understand what gradient descent is

Gradient descent is the source of power for machine learning
After the previous two sections, we can start to talk about the source of power for machine learning: gradient descent .
Gradient descent is not a very complicated mathematical tool. Its history has been more than 200 years. However, people may not have expected that such a relatively simple mathematical tool will become the basis of many machine learning algorithms, and it also has a history of more than 200 years. Together with neural networks, it ignited the deep learning revolution.
1. What is gradient
Find the partial derivatives of each parameter of the multivariate function, and then write the obtained partial derivatives of each parameter in the form of a vector, which is the gradient.
Specifically, the function f (x1, x2) of the two independent variables corresponds to the two features in the machine learning data set. If the partial derivatives are obtained for x1 and x2 respectively, then the obtained gradient vector It is (∂f/∂x1, ∂f/∂x2) T, which can be expressed mathematically as Δf (x1, x2). So what is the point of calculating the gradient vector? Its geometric meaning is the direction in which the function changes, and it is the fastest changing direction. For function f(x), at point (x0, y0), the direction of the gradient vector is the direction in which the y value increases fastest. In other words, along the direction of the gradient vector Δf (x0), the maximum value of the function can be found. On the other hand, along the opposite direction of the gradient vector, that is, the direction of -Δf(x0), the gradient decreases fastest and the minimum value of the function can be found. If the value of the gradient vector at a certain point is 0, then it has reached the lowest point (or local lowest point) of the function with a derivative of 0.
2. Gradient Descent: The Metaphor of Downhill
It is very common to use downhill as a metaphor for gradient descent in machine learning. Imagine that you are standing somewhere on a large mountain, looking at the endless terrain in the distance, only knowing that the location in the distance is much lower than here. You want to know how to go down the mountain, but you can only go down step by step, that is, every time you reach a position, find the gradient of the current position. Then, take a step down along the negative direction of the gradient, that is, go down the steepest place, continue to solve the gradient of the new position, and continue to take a step down along the steepest place at the new position. Just walk step by step until you reach the bottom of the mountain, as shown in the picture below.

From the above explanation, it is not difficult to understand why we just mentioned the concavity and convexity of the function. Because, in a non-convex function, it may not reach the bottom of the mountain, but stop at a certain valley. In other words, gradient descent for non-convex functions may not always find the global optimal solution, and may only obtain a local optimal solution. However, if the function is convex, then the gradient descent method can theoretically obtain the global optimal solution.
3. What is the use of gradient descent?
Gradient descent is very useful in machine learning. Simply put, you can pay attention to the following points.
The essence of machine learning is to find the optimal function.
How to measure whether a function is optimal? The method is to minimize the error between the predicted value and the true value (also called the loss value in machine learning).
You can establish a function between the error and model parameters (preferably a convex function).
Gradient descent can guide us to the global lowest point of the convex function, that is, to find the parameters with the smallest error.
The above is the detailed content of This article will help you understand what gradient descent is. For more information, please follow other related articles on the PHP Chinese website!
 What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AM
What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AMIntroduction In prompt engineering, “Graph of Thought” refers to a novel approach that uses graph theory to structure and guide AI’s reasoning process. Unlike traditional methods, which often involve linear s
 Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AM
Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AMIntroduction Congratulations! You run a successful business. Through your web pages, social media campaigns, webinars, conferences, free resources, and other sources, you collect 5000 email IDs daily. The next obvious step is
 Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AM
Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AMIntroduction In today’s fast-paced software development environment, ensuring optimal application performance is crucial. Monitoring real-time metrics such as response times, error rates, and resource utilization can help main
 ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM
ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM“How many users do you have?” he prodded. “I think the last time we said was 500 million weekly actives, and it is growing very rapidly,” replied Altman. “You told me that it like doubled in just a few weeks,” Anderson continued. “I said that priv
 Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AM
Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AMIntroduction Mistral has released its very first multimodal model, namely the Pixtral-12B-2409. This model is built upon Mistral’s 12 Billion parameter, Nemo 12B. What sets this model apart? It can now take both images and tex
 Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AM
Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AMImagine having an AI-powered assistant that not only responds to your queries but also autonomously gathers information, executes tasks, and even handles multiple types of data—text, images, and code. Sounds futuristic? In this a
 Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AM
Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AMIntroduction The finance industry is the cornerstone of any country’s development, as it drives economic growth by facilitating efficient transactions and credit availability. The ease with which transactions occur and credit
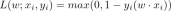 Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AM
Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AMIntroduction Data is being generated at an unprecedented rate from sources such as social media, financial transactions, and e-commerce platforms. Handling this continuous stream of information is a challenge, but it offers an


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool

Zend Studio 13.0.1
Powerful PHP integrated development environment

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

SublimeText3 Mac version
God-level code editing software (SublimeText3)

VSCode Windows 64-bit Download
A free and powerful IDE editor launched by Microsoft






