How to implement the top ten sorting algorithms in Java

Stability of sorting algorithm:

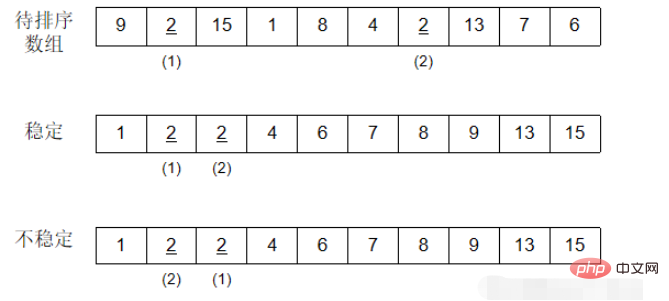
It is assumed that there are multiple records with the same keywords in the record sequence to be sorted. After sorting, these records are guaranteed to be The relative order of records remains unchanged, that is, in the original sequence, a[i]=a[j], and a[i] is before a[j]. After sorting, it is guaranteed that a[i] is still before a[j]. Then this sorting algorithm is called stable; otherwise it is called unstable.

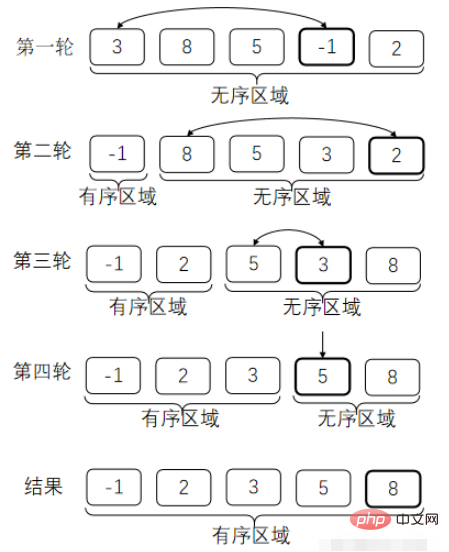
1. Selection sorting

Each time, select the smallest element from the elements to be sorted, and place it in sequence with the 1st, 2nd, 3rd... elements are exchanged. This forms an ordered area at the front of the array. Each time a swap is performed, the length of the ordered region is increased by one.

public static void selectionSort(int[] arr){
    //细节一：这里可以是arr.length也可以是arr.length-1
    for (int i = 0; i < arr.length-1 ; i++) {
        int mini = i;
        for (int j = i+1; j < arr.length; j++) {
            //切换条件，决定升序还是降序
            if(arr[mini]>arr[j]) mini =j;
        }
        swap(arr,mini,i);
    }
}

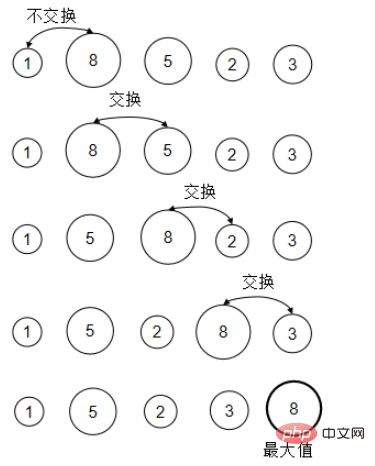
2. Bubble sorting

Compare two adjacent numbers in turn. If they are in the wrong order, swap them. In this case, each After rounds of comparison, you can put the largest number where it should be. (It’s like bringing the biggest bubble to the top)

Here is an explanation of the meaning of the wrong order. We sort in ascending order. The later values ​​should be greater than or equal to the previous values. If not, swap them.

public static void bubbleSort(int[] arr){
    for (int i = 0; i < arr.length-1; i++) {
        //记录本次有没有进行交换的操作
        boolean flag = false;
        //保存在头就动头，保存在尾就动尾
        for(int j =0 ; j < arr.length-1-i ; j++){
            //升序降序选择地
            if(arr[j] > arr[j+1])
            {
                swap(arr,j,j+1);
                flag = true;
            }
        }
        //如果本次没有进行交换操作，表示数据已经有序
        if(!flag){break;} //程序结束
    }
}

3. Insertion sort

Insertion sort can actually be understood as the process of drawing cards when we play poker. The cards are always in order, and every time a card is touched, the card is inserted where it should be. After all the cards have been touched, all the cards will be in order.

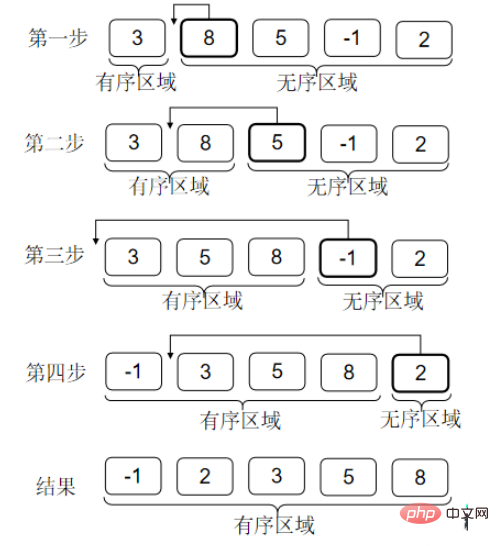
Thoughts: An ordered area is formed in front of the array. When I look for the position where the current number should be inserted, I use binary division. Can I reduce the complexity of insertion sort? Has it been optimized to O(nlogn)?

                                                                                                                                                                       The position can be found with the complexity of log. The key is that if you use an array to store the data, the complexity of moving the data back during insertion is still O(n). If you use a linked list, finding the position and inserting it is O(1), but the linked list cannot be divided into two.

public static void insertSort(int[] arr){
        //从第二个数开始，把每个数依次插入到指定的位置
        for(int i = 1 ; i < arr.length ; i++)
        {
            int key = arr[i];
            int j = i-1;
            //大的后移操作
            while(j >= 0 && arr[j] > key)
            {
                arr[j+1] = arr[j];
                j--;
            }
            arr[j+1] = key;
        }
    }

4. Hill sorting

Hill sorting is a sorting algorithm proposed by Donald Shell in 1959. It is an improved and efficient version of direct insertion sorting. Hill sorting requires preparing a set of data as an incremental sequence.

This set of data needs to meet the following three conditions:

1. The data is arranged in descending order

2. The maximum value in the data is less than the length of the array to be sorted

3. The minimum value in the data is 1.

As long as the array meets the above requirements, it can be used as an incremental sequence, but different incremental sequences will affect the efficiency of sorting. Here we use {5,3,1} as the incremental sequence to explain

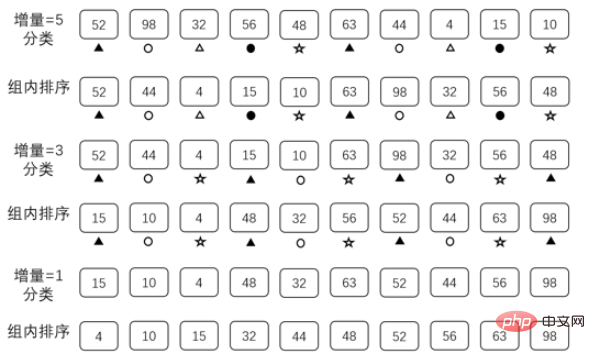
The reason for achieving optimization: reduce the amount of data, so that O(n) and O(n ^2) The gap is not big

public static void shellSort(int[] arr){
        //分块处理
        int gap = arr.length/2; //增量
        while(1<=gap)
        {
            //插入排序：只不过是与增量位交换
            for(int i = gap ; i < arr.length ; i++)
            {
                int key = arr[i];
                int j = i-gap;
                while(j >= 0 && arr[j] > key)
                {
                    arr[j+gap] = arr[j];
                    j-=gap;
                }
                arr[j+gap] = key;
            }
            gap = gap/2;
        }
    }

5. Heap sort

is a complete binary tree, divided into two types: large root heap and small root heap

can be O( 1) Take the maximum/minimum value, delete the maximum/minimum value in O(logn), and insert the element in O(logn)

MIN-HEAPIFY (i) Operation:

We assume a complete binary tree Both the left subtree and the right subtree of a certain node i satisfy the properties of a small root heap. Assume that the left child of node i is left_i, and the right child of node i is rigℎt_i. If a[i] is larger than a[left_i] or a[rigℎt_i], then the entire subtree with i node as the root node will not satisfy the properties of a small root heap. We now need to perform an operation: put i as the root node The subtree of the root node is adjusted into a small root heap.

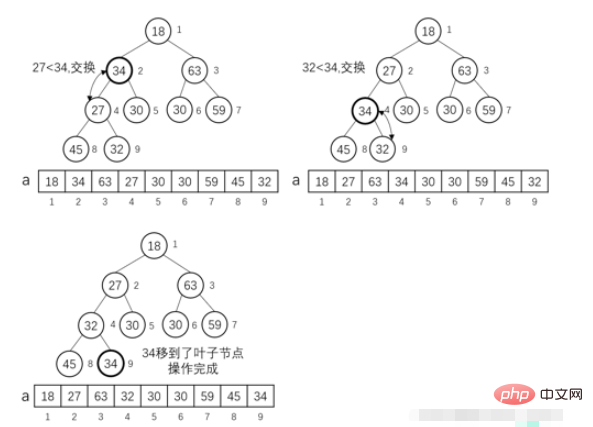
//堆排序
    public static void heapSort(int[] arr){
        //开始调整的位置为最后一个叶子节点
        int start = (arr.length - 1)/2;
        //从最后一个叶子节点开始遍历，调整二叉树
        for (int i = start; i >= 0 ; i--){
            maxHeap(arr, arr.length, i);
        }
 
        for (int i = arr.length - 1; i > 0; i--){
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
            maxHeap(arr, i, 0);
        }
    }
 
    //将二叉树调整为大顶堆
    public static void maxHeap(int[] arr, int size, int index){
        //建立左子节点
        int leftNode = 2 * index + 1;
        //建立右子节点
        int rightNode = 2 * index + 2;
 
        int maxNode = index;
        //左子节点的值大于根节点时调整
        if (leftNode < size && arr[leftNode] > arr[maxNode]){
            maxNode = leftNode;
        }
        //右子节点的值大于根节点时调整
        if (rightNode < size && arr[rightNode] > arr[maxNode]){
            maxNode = rightNode;
        }
        if (maxNode != index){
            int temp = arr[maxNode];
            arr[maxNode] = arr[index];
            arr[index] = temp;
            //交换之后可能会破坏原来的结构，需要再次调整
            //递归调用进行调整
            maxHeap(arr, size, maxNode);
        }
    }

I use a large root heap. The sorting process boils down to: first the left root and then the right root (depend on how you write it) ->Each root Up is down. (Left, right, up and down)

6. Merge sort

Merge sort is a typical application of the divide and conquer method. Let’s first introduce the divide and conquer method. The divide and conquer method is to divide a complex problem into two or more identical or similar sub-problems, and then divide the sub-problems into smaller sub-problems...until the final sub-problem is small enough to be solved directly, and then combine the solutions to the sub-problems to get the solution to the original problem .

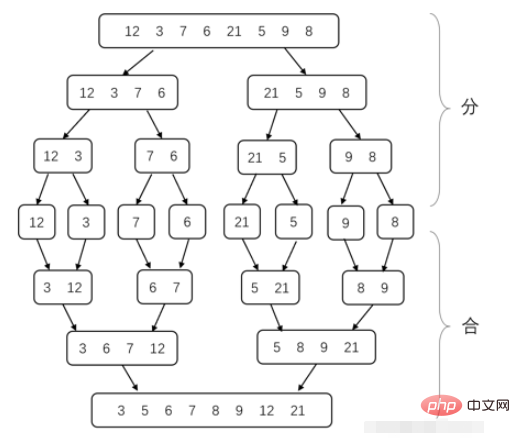
The process of merge sort decomposition sub-problem is to divide the array into 2 parts each time until the length of the array is 1 (because an array with only one number is ordered). Then merge adjacent ordered arrays into one ordered array. Until they are all put together, the entire array is sorted. The problem to be solved now is how to merge two ordered arrays into one ordered array. In fact, it is to compare the two smallest current elements of the two arrays every time, and choose whichever is smaller

##1,3,42,5,7##2,5,71,3,44

1,2, 3,4##1,3,42,5,71,3,4

Array a

Array b

Explanation

Answer array

##2,5 ,7

##1

1

1,3,4

2

1,2

1,3,4

##3

1,2,3

##2,5,7

##2,5,7

There are no elements in array b, take 5

1,2,3,4,5

There are no elements in array b, take 7

1,2,3,4,5,7

public static void mergeSort(int[] arr, int low, int high){
        int middle = (high + low)/2;
        if (low < high){
            //递归排序左边
            mergeSort(arr, low, middle);
            //递归排序右边
            mergeSort(arr, middle +1, high);
            //将递归排序好的左右两边合并
            merge(arr, low, middle, high);
        }
 
    }
 
    public static void merge(int[] arr, int low, int middle, int high){
        //存储归并后的临时数组
        int[] temp = new int[high - low + 1];
        int i = low;
        int j = middle + 1;
        //记录临时数组中存放数字的下标
        int index = 0;
        while (i <= middle && j <= high){
            if (arr[i] < arr[j]){
                temp[index] = arr[i];
                i++;
            } else {
                temp[index] = arr[j];
                j++;
            }
            index++;
        }
        //处理剩下的数据
        while (j <= high){
            temp[index] = arr[j];
            j++;
            index++;
        }
        while (i <= middle){
            temp[index] = arr[i];
            i++;
            index++;
        }
        //将临时数组中的数据放回原来的数组
        for (int k = 0; k < temp.length; ++k){
            arr[k + low] = temp[k];
        }
    }

七.快速排序

        快速排序的工作原理是：从待排序数组中随便挑选一个数字作为基准数，把所有比它小的数字放在它的左边，所有比它大的数字放在它的右边。然后再对它左边的数组和右边的数组递归进行这样的操作。

        全部操作完以后整个数组就是有序的了。 把所有比基准数小的数字放在它的左边，所有比基准数大的数字放在它的右边。这个操作，我们称为“划分”(Partition)。

	//快速排序
	public static void QuickSort1(int[] arr, int start, int end){
		int low = start, high = end;
		int temp;
		if(start < end){
		    int guard = arr[start];
			while(low != high){
				while(high > low && arr[high] >= guard) high--;
				while(low < high && arr[low] <= guard) low++;
				if(low < high){
					temp = arr[low];
					arr[low] = arr[high];
					arr[high] = temp;
				}
			}
			arr[start] = arr[low];
			arr[low] = guard;
			QuickSort1(arr, start, low-1);
			QuickSort1(arr, low+1, end);
		}
	}
	
	//快速排序改进版(填坑法)
	public static void QuickSort2(int[] arr, int start, int end){
		int low = start, high = end;
		if(start < end){
		while(low != high){
	    	int guard = arr[start];//哨兵元素
			while(high > low && arr[high] >= guard) high--;
			arr[low] = arr[high];
			while(low < high && arr[low] <= guard) low++;
			arr[high] = arr[low];
		}
		arr[low] = guard;
		QuickSort2(arr, start, low-1);
		QuickSort2(arr, low+1, end);
	}
}

八.鸽巢排序

        计算一下每一个数出现了多少次。举一个例子，比如待排序的数据中1出现了2次，2出现了0次，3出现了3次，4出现了1次，那么排好序的结果就是{1.1.3.3.3.4}。

//鸽巢排序
    public static void PigeonholeSort(int[] arr){
        //获取最大值
        int k = 0;
        for (int i = 0; i < arr.length; i++) {
            k = Math.max(k,arr[i]);
        }
        //创建计数数组并且初始化为0
        int[] cnt = new int[k+10];
        for(int i = 0 ; i <= k ; i++) { cnt[i]=0; }
        for(int i = 0 ; i < arr.length ;i++) { cnt[arr[i]]++; }
        int j = 0;
        for(int i = 0 ; i <=k ; i++)
        {
            while(cnt[i]!=0)
            {
                arr[j]=i;
                j++;
                cnt[i]--;
            }
        }
    }

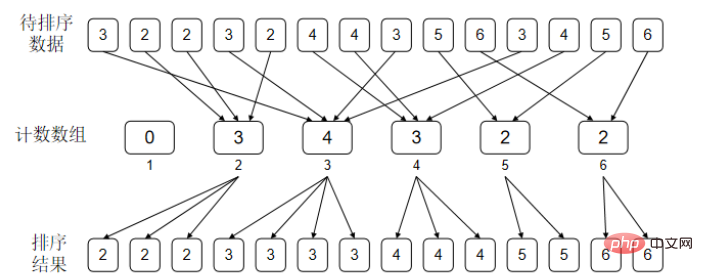
        鸽巢排序其实算不上是真正意义上的排序算法，它的局限性很大。只能对纯整数数组进行排序，举个例子，如果我们需要按学生的成绩进行排序。是一个学生+分数的结构那就不能排序了。

九.计数排序

        先考虑这样一个事情：如果对于待排序数据中的任意一个元素 a[i]，我们知道有 m 个元素比它小，那么我们是不是就可以知道排好序以后这个元素应该在哪个位置了呢？（这里先假设数据中没有相等的元素）。计数排序主要就是依赖这个原理来实现的。

比如待排序数据是{2,4,0,2,4} 先和鸽巢一样做一个cnt数组{1,0,2,0,2}                                                                                                                                    0,1,2,3,4

此时cnt[i]表示数据i出现了多少次，

然后对cnt数组做一个前缀和{1,1,3,3,5}    ：0,1,2,3,4

此时cnt[i]表示数据中小于等于i的数字有多少个

待排序数组	计数数组	说明	答案数组ans
2,4,0,2,4	1,1,3,3,5	初始状态	null,null,null,null,null,
2,4,0,2,4	1,1,3,3,5	cnt[4]=5，ans第5位赋值，cnt[4]-=1	null,null,null,null,4
2,4,0,2,4	1,1,3,3,4	cnt[2]=3，ans第3位赋值，cnt[2]-=1	null,null,2 null,4
2,4,0,2,4	1,1,2,3,4	cnt[0]=1，ans第1位赋值，cnt[0]-=1	0,null,2,null,4
2,4,0,2,4	0,1,2,3,4	cnt[4]=4，ans第4位赋值，cnt[4]-=1	0,null,2,4,4
2,4,0,2,4	0,1,2,3,3	cnt[2]=2，ans第2位赋值，cnt[2]-=1	0,2,2,4,4

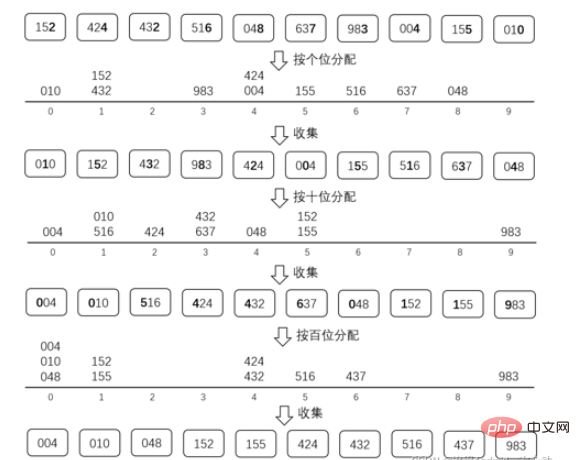
十.基数排序

基数排序是通过不停的收集和分配来对数据进行排序的。

• 因为是10进制数，所以我们准备十个桶来存分配的数。

• 最大的数据是3位数，所以我们只需要进行3次收集和分配。

• 需要先从低位开始收集和分配（不可从高位开始排，如果从高位开始排的话，高位排好的顺序会在排低位的时候被打乱，有兴趣的话自己手写模拟一下试试就可以了）

• 在收集和分配的过程中，不要打乱已经排好的相对位置

        比如按十位分配的时候，152和155这两个数的10位都是5，并且分配之前152在155的前面，那么收集的时候152还是要放在155之前的。

//基数排序
    public static void radixSort(int[] array) {
        //基数排序
        //首先确定排序的趟数;
        int max = array[0];
        for (int i = 1; i < array.length; i++) {
            if (array[i] > max) {
                max = array[i];
            }
        }
        int time = 0;
        //判断位数;
        while (max > 0) {
            max /= 10;
            time++;
        }
        //建立10个队列;
        List<ArrayList> queue = new ArrayList<ArrayList>();
        for (int i = 0; i < 10; i++) {
            ArrayList<Integer> queue1 = new ArrayList<Integer>();
            queue.add(queue1);
        }
        //进行time次分配和收集;
        for (int i = 0; i < time; i++) {
            //分配数组元素;
            for (int j = 0; j < array.length; j++) {
                //得到数字的第time+1位数;
                int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
                ArrayList<Integer> queue2 = queue.get(x);
                queue2.add(array[j]);
                queue.set(x, queue2);
            }
            int count = 0;//元素计数器;
            //收集队列元素;
            for (int k = 0; k < 10; k++) {
                while (queue.get(k).size() > 0) {
                    ArrayList<Integer> queue3 = queue.get(k);
                    array[count] = queue3.get(0);
                    queue3.remove(0);
                    count++;
                }
            }
 
        }
 
 
    }

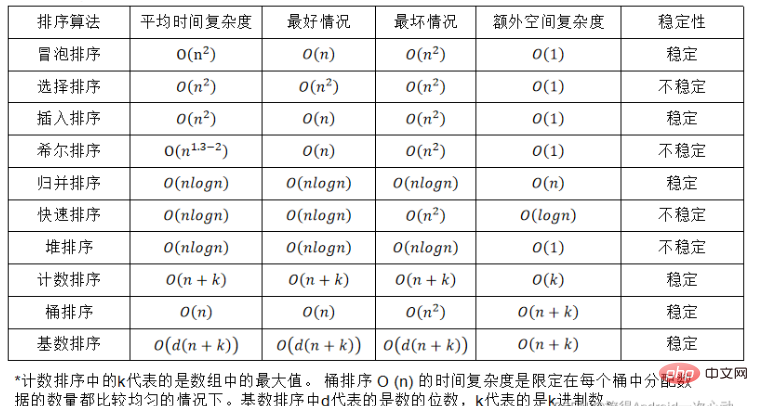
The above is the detailed content of How to implement the top ten sorting algorithms in Java. For more information, please follow other related articles on the PHP Chinese website!