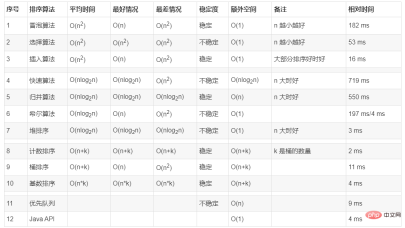
Summary:
1. Bubble sort
Determine the best value in each round of loop;
public void bubbleSort(int[] nums){
int temp;
boolean isSort = false; //优化,发现排序好就退出
for (int i = 0; i < nums.length-1; i++) {
for (int j = 0; j < nums.length-1-i; j++) { //每次排序后能确定较大值
if(nums[j] > nums[j+1]){
isSort = true;
temp = nums[j];
nums[j] = nums[j+1];
nums[j+1] = temp;
}
}
if(!isSort){
return;
} else {
isSort = false;
}
}
}2. Selection sort
Select the best value each time and swap it to the edge;
public void selectSort(int[] nums){
for (int i = 0; i < nums.length-1; i++) {
int index = i;
int minNum = nums[i];
for (int j = i+1; j < nums.length; j++) {
if(nums[j] < minNum){
minNum = nums[j];
index = j;
}
}
if(index != i){
nums[index] = nums[i];
nums[i] = minNum;
}
}
}3. Insertion sort
Find its own position for each number in the loop and insert it;
public void insertionSort(int[] nums){
for (int i = 1; i < nums.length; i++) {
int j = i;
int insertNum = nums[i];
while(j-1 >= 0 && nums[j-1] > insertNum){
nums[j] = nums[j-1];
j--;
}
nums[j] = insertNum;
}
}4. Quick sort
Select a basic value that is smaller than it Put it on one side, and put the larger one on the other side;
public void quickSortDfs(int[] nums, int left, int right){
if(left > right){
return;
}
int l = left;
int r = right;
int baseNum = nums[left];
while(l < r){
//必须右边先走
while(nums[r] >= baseNum && l < r){
r--;
}
while(nums[l] <= baseNum && l < r){
l++;
}
int temp = nums[l];
nums[l] = nums[r];
nums[r] = temp;
}
nums[left] = nums[l];
nums[l] = baseNum;
quickSortDfs(nums, left, r-1);
quickSortDfs(nums, l+1, right);
}5. Merge sort
Divide and conquer algorithm;
//归
public void mergeSortDfs(int[] nums, int l, int r){
if(l >= r){
return;
}
int m = (l+r)/2;
mergeSortDfs(nums, l, m);
mergeSortDfs(nums, m+1, r);
merge(nums, l, m, r);
}
//并
private void merge(int[] nums, int left, int mid, int right){
int[] temp = new int[right-left+1];
int l = left;
int m = mid+1;
int i = 0;
while(l <= mid && m <= right){
if(nums[l] < nums[m]){
temp[i++] = nums[l++];
} else {
temp[i++] = nums[m++];
}
}
while(l <= mid){
temp[i++] = nums[l++];
}
while(m <= right){
temp[i++] = nums[m++];
}
System.arraycopy(temp, 0, nums, left, temp.length);
}6. Er sort
Introducing step size to reduce the number of number exchanges and improve efficiency;
6.1 Hill-bubble sort (slow)
public void shellBubbleSort(int[] nums){
for (int step = nums.length/2; step > 0 ; step /= 2) {
for (int i = step; i < nums.length; i++) {
for (int j = i-step; j >= 0; j -= step) {
if(nums[j] > nums[j+step]){
int temp = nums[j];
nums[j] = nums[j+step];
nums[j+step] = temp;
}
}
}
}
}6.2 Hill -Insertion sort (fast)
public void shellInsertSort(int[] nums){
for (int step = nums.length/2; step > 0; step /= 2) {
for (int i = step; i < nums.length; i++) {
int j = i;
int insertNum = nums[i];
while(j-step >= 0 && nums[j-step] > insertNum){
nums[j] = nums[j-step];
j-=step;
}
nums[j] = insertNum;
}
}
}7. Heap sort
Big top heap implements ascending order, moving the maximum value to the last position of the heap each time;
public void heapSort2(int[] nums) {
for(int i = nums.length/2-1; i >= 0; i--){
sift(nums, i, nums.length);
}
for (int i = nums.length-1; i > 0; i--) {
int temp = nums[0];
nums[0] = nums[i];
nums[i] = temp;
sift(nums, 0, i);
}
}
private void sift(int[] nums, int parent, int len) {
int value = nums[parent];
for (int child = 2*parent +1; child < len; child = child*2 +1) {
if(child+1 < len && nums[child+1] > nums[child]){
child++;
}
if(nums[child] > value){
nums[parent] = nums[child];
parent = child;
} else {
break;
}
}
nums[parent] = value;
}8. Counting sorting
Count the occurrences of each number in order;
public void countSort(int[] nums){
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int num : nums){
max = Math.max(max, num);
min = Math.min(min, num);
}
int[] countMap = new int[max-min+1];
for(int num : nums){
countMap[num-min]++;
}
int i = 0;
int j = 0;
while(i < nums.length && j < countMap.length){
if(countMap[j] > 0){
nums[i] = j+min;
i++;
countMap[j]--;
} else {
j++;
}
}
}9. Bucket sorting
Similar to counting sorting, the difference is that the statistics are the numbers in a certain interval (bucket);
public void bucketSort(int[] nums){
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int num : nums){
max = Math.max(max, num);
min = Math.min(min, num);
}
int bucketCount = (max-min)/nums.length+1;
List<List<Integer>> bucketList = new ArrayList<>();
for (int i = 0; i < bucketCount; i++) {
bucketList.add(new ArrayList<>());
}
for(int num : nums){
int index = (num-min)/nums.length;
bucketList.get(index).add(num);
}
for(List<Integer> bucket : bucketList){
Collections.sort(bucket);
}
int j = 0;
for(List<Integer> bucket : bucketList){
for(int num : bucket){
nums[j] = num;
j++;
}
}
}10. Cardinal sorting
By ones, tens, hundreds Bits are sorted in order;
public void radixSort(int[] nums){
int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
for (int num : nums) {
min = Math.min(min, num);
max = Math.max(max, num);
}
for (int i = 0; i < nums.length; i++) {
nums[i] -= min;
}
max -= min;
int maxLen = (max+"").length();
int[][] bucket = new int[nums.length][10];
int[] bucketCount = new int[10];
for (int i = 0, n = 1; i < maxLen; i++, n*=10) {
for (int num : nums) {
int digitVal = num / n % 10;
bucket[bucketCount[digitVal]][digitVal] = num;
bucketCount[digitVal]++;
}
int index = 0;
for (int j = 0; j < bucketCount.length; j++) {
if(bucketCount[j] > 0){
for (int k = 0; k < bucketCount[j]; k++) {
nums[index] = bucket[k][j];
index++;
}
}
bucketCount[j] = 0;
}
}
for (int i = 0; i < nums.length; i++) {
nums[i] += min;
}
}11. Using collections or API
11.1 Priority queue
public void priorityQueueSort(int[] nums){
PriorityQueue<Integer> queue = new PriorityQueue<>();
for(int num : nums){
queue.offer(num);
}
for (int i = 0; i < nums.length; i++) {
nums[i] = queue.poll();
}
}11.2 Java API
public void arraysApiSort(int[] nums){
Arrays.sort(nums);
}The above is the detailed content of How to implement common sorting algorithms in Java. For more information, please follow other related articles on the PHP Chinese website!
 How to get Java entity class attribute names elegantly to avoid hard-coded in MyBatis queries?Apr 19, 2025 pm 08:27 PM
How to get Java entity class attribute names elegantly to avoid hard-coded in MyBatis queries?Apr 19, 2025 pm 08:27 PMWhen using MyBatis-Plus or tk.mybatis...
 How to efficiently query personnel data in MySql and ElasticSearch through natural language processing?Apr 19, 2025 pm 08:24 PM
How to efficiently query personnel data in MySql and ElasticSearch through natural language processing?Apr 19, 2025 pm 08:24 PMHow to query personnel data through natural language processing? In modern data processing, how to efficiently query personnel data is a common and important requirement. ...
 How to parse next-auth generated JWT token in Java and get information in it?Apr 19, 2025 pm 08:21 PM
How to parse next-auth generated JWT token in Java and get information in it?Apr 19, 2025 pm 08:21 PMIn processing next-auth generated JWT...
 How to package in IntelliJ IDEA for specific Git versions to avoid including unfinished code?Apr 19, 2025 pm 08:18 PM
How to package in IntelliJ IDEA for specific Git versions to avoid including unfinished code?Apr 19, 2025 pm 08:18 PMIn IntelliJ...
 Why can't JavaScript directly obtain hardware information on the user's computer?Apr 19, 2025 pm 08:15 PM
Why can't JavaScript directly obtain hardware information on the user's computer?Apr 19, 2025 pm 08:15 PMDiscussion on the reasons why JavaScript cannot obtain user computer hardware information In daily programming, many developers will be curious about why JavaScript cannot be directly obtained...
 Circular dependencies appear in the RuoYi framework. How to troubleshoot and solve the problem of dynamicDataSource Bean?Apr 19, 2025 pm 08:12 PM
Circular dependencies appear in the RuoYi framework. How to troubleshoot and solve the problem of dynamicDataSource Bean?Apr 19, 2025 pm 08:12 PMRuoYi framework circular dependency problem troubleshooting and solving the problem of circular dependency when using RuoYi framework for development, we often encounter circular dependency problems, which often leads to the program...
 When building a microservice architecture using Spring Cloud Alibaba, do you have to manage each module in a parent-child engineering structure?Apr 19, 2025 pm 08:09 PM
When building a microservice architecture using Spring Cloud Alibaba, do you have to manage each module in a parent-child engineering structure?Apr 19, 2025 pm 08:09 PMAbout SpringCloudAlibaba microservices modular development using SpringCloud...
 Treatment of x² in curve integral: Why can the standard answer be ignored (1/3) x³?Apr 19, 2025 pm 08:06 PM
Treatment of x² in curve integral: Why can the standard answer be ignored (1/3) x³?Apr 19, 2025 pm 08:06 PMQuestions about a curve integral This article will answer a curve integral question. The questioner had a question about the standard answer to a sample question...


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SublimeText3 Linux new version
SublimeText3 Linux latest version

Dreamweaver Mac version
Visual web development tools

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.

SublimeText3 Mac version
God-level code editing software (SublimeText3)






