Example analysis of union-find in java

1. Overview

Union-find: a tree data structure used to solve some merging and query problems of disjoint sets. For example: there are n villages, query whether there is a connecting road between the two villages, connecting the two villages

Two cores:

Find: Find the set where the element is located

Merge (Union): Merge the sets of two elements into one set

2. Implementation

There are two common implementation ideas

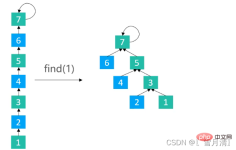
Quick Find

• Find time complexity: O(1)

• Union time Complexity: O(n)

Quick Union

• Time complexity of Find: O(logn) Can be optimized to O(a(n))a(n)

• Time complexity of merge (Union): O(logn) can be optimized to O(a(n) )) a(n)

Use an array to implement a tree structure. The array subscript is the element, and the value stored in the array is the value of the parent node

Create abstract class Union Find

public abstract class UnionFind {
 
	 int[] parents;
	/**
	 * 初始化并查集
	 * @param capacity
	 */
	public UnionFind(int capacity){
		
		if(capacity < 0) {
			throw new IllegalArgumentException("capacity must be >=0");
		}
        //初始时每一个元素父节点（根结点）是自己
		parents = new int[capacity];
		for(int i = 0; i < parents.length;i++) {
			parents[i] = i;
		}
	}
	
   /**
     *  检查v1 v2 是否属于同一个集合
     */
	public boolean isSame(int v1,int v2) {
		return find(v1) == find(v2);
	}
 
    /**
     *  查找v所属的集合 （根节点）
     */
	public  abstract int find(int v);
 
	/**
     *  合并v1 v2 所属的集合
     */
	public abstract void union(int v1, int v2);
	
		
	// 范围检查
	public   void rangeCheck(int v)  {
		if(v<0 || v > parents.length)
			throw new IllegalArgumentException("v is out of capacity");
	}
}

2.1 Quick Find implementation

Using Quick Find to implement union find, the maximum height of the tree is 2, and the height of each node is The parent node is the root node

public class UnionFind_QF extends UnionFind {
	public UnionFind_QF(int capacity) {
		super(capacity);
		
	}
 
  // 查
@Override
	public  int  find(int v) {
		rangeCheck(v);
		return parents[v];
	}
 
 // 并 将v1所在集合并到v2所在集合上
@Override
public void union(int v1, int v2) {
    // 查找v1 v2 的父（根）节点
	int p1= find(v1);
	int p2 = find(v2);
	if(p1 == p2) return;
  
    //将所有以v1的根节点为根节点的元素全部并到v2所在集合上 即父节点改为v2的父节点
	for(int i = 0; i< parents.length; i++) {
		if(parents[i] == p1) {
			parents[i] = p2;
		}
	}
	
  }
}

2.2 Quick Union implementation

public class UnionFind_QU extends UnionFind {
 
	public UnionFind_QU(int capacity) {
		super(capacity);
		
	}
 
	//查某一个元素的根节点
	@Override
	public int find(int v) {
   //检查下标是否越界
		rangeCheck(v);
   
  // 一直循环查找节点的根节点
		while (v != parents[v]) {
			v = parents[v];
		}
		return v;
	}
 
//V1 并到 v2 中
	@Override
	public void union(int v1, int v2) {
	
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
      //将v1 根节点 的 父节点 修改为 v2的根结点 完成合并
		parents[p1] = p2;
	}
}

3. Optimization

Union lookup is often implemented by fast union, but fast union sometimes causes tree imbalance.

There are two optimization ideas: rank optimization and size optimization

3.1 Size-based optimization

Core idea: A tree with few elements is grafted to a tree with many elements

public class UniondFind_QU_S extends UnionFind{
 
   // 创建sizes 数组记录 以元素（下标）为根结点的元素（节点）个数
	private int[] sizes;
 
	public UniondFind_QU_S(int capacity) {
		super(capacity);
 
		sizes = new int[capacity];
 
   //初始都为 1
		for(int i = 0;i < sizes.length;i++) {
			sizes[i] = 1;
			}
		
	}
 
	@Override
	public int find(int v) {
 
		rangeCheck(v);
 
		while (v != parents[v]) {
			v = parents[v];
		}
		return v;
	}
 
	@Override
	public void union(int v1, int v2) {
	
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
 
		//如果以p1为根结点的元素个数 小于 以p2为根结点的元素个数 p1并到p2上，并且更新p2为根结点的元素个数
	if(sizes[p1] < sizes[p2]) {
		    parents[p1] = p2;
		    sizes[p2] += sizes[p1];
		
 // 反之 则p2 并到 p1 上，更新p1为根结点的元素个数
	}else {
			parents[p2] = p1;
			sizes[p1] += sizes[p2];
		}
	}
}

Size-based optimization may also lead to tree imbalance

3.2 Based on rank optimization

Core idea: grafting a short tree to a tall tree

public class UnionFind_QU_R extends UnionFind_QU {
   // 创建rank数组  ranks[i] 代表以i为根节点的树的高度
 private int[] ranks;
 
	public UnionFind_QU_R(int capacity) {
		super(capacity);
 
		ranks = new int[capacity];
 
		for(int i = 0;i < ranks.length;i++) {
			ranks[i] = 1;
		}
 
	}
    
	public void union(int v1, int v2) {
 
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
    
    // p1 并到 p2 上 p2为根 树的高度不变
		if(ranks[p1] < ranks[p2]) {
			parents[p1] = p2;
			
  // p2 并到 p1 上 p1为根 树的高度不变
		} else if(ranks[p1] > ranks[p2]) {
			parents[p2] = p1;
 
		}else {
    // 高度相同 p1 并到 p2上，p2为根 树的高度+1
			parents[p1] = p2;
			ranks[p2] += 1;
		}
	}
}

Based on rank optimization, as the number of Unions increases, the height of the tree will still get higher and higher, leading to find The operation slows down

There are three ideas to continue optimizing: path compression, path splitting, and path halving

3.2.1 Path Compression (Path Compression)

Use it when finding All nodes on the path point to the root node, thereby reducing the height of the tree

/**
 *  Quick Union -基于rank的优化  -路径压缩
 *
 */
public class UnionFind_QU_R_PC extends UnionFind_QU_R {
 
	public UnionFind_QU_R_PC(int capacity) {
		super(capacity);
		
	}
 
	@Override
	public int find(int v) {
		rangeCheck(v);
 
		if(parents[v] != v) {
 
        //递归 使得从当前v 到根节点 之间的 所有节点的 父节点都改为根节点
			parents[v] = find(parents[v]);
		}
		return parents[v];
	}
}

Although the height of the tree can be reduced, the implementation cost is slightly higher

3.2 .2 Path Spliting

Make every node on the path point to its grandparent node

/**
 *  Quick Union -基于rank的优化  -路径分裂
 *
 */
public class UnionFind_QU_R_PS extends UnionFind_QU_R {
 
	public UnionFind_QU_R_PS(int capacity) {
		super(capacity);
		
	}
 
	@Override
	public int find(int v) {
		rangeCheck(v);
		while(v != parents[v]) {
 
			int p = parents[v];
			parents[v] = parents[parents[v]];
			v = p;
		}
		return v;
	}
}

3.2.3 Path halved (Path Halving)

Make every other node on the path point to its grandparent node

/**
 *  Quick Union -基于rank的优化  -路径减半
 *
 */
public class UnionFind_QU_R_PH extends UnionFind_QU_R {
 
	public UnionFind_QU_R_PH(int capacity) {
		super(capacity);
		
	}
	
	
    public int find(int v) {
    	rangeCheck(v);
 
		while(v != parents[v]) {
			parents[v] = parents[parents[v]];
			v = parents[v];
		}
		return v;
	}	 
 }

Use Quick Union to optimize the path split or path halving based on rank

It can be guaranteed that the amortized time complexity of each operation is O(a(n)), a(n)

The above is the detailed content of Example analysis of union-find in java. For more information, please follow other related articles on the PHP Chinese website!