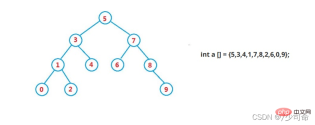
 Java
Java javaTutorial
javaTutorial Detailed explanation of examples of adding, inserting, deleting and creating Java binary search trees
Detailed explanation of examples of adding, inserting, deleting and creating Java binary search trees①Concept
Binary search tree is also called binary sorting tree. It is either an empty tree** or has the following properties Binary tree:
If its left subtree is not empty, then the values of all nodes on the left subtree are less than the value of the root node
If its right subtree is not empty, then The values of all nodes on the right subtree are greater than the value of the root node
Its left and right subtrees are also binary search trees
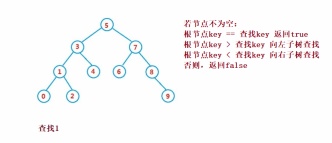
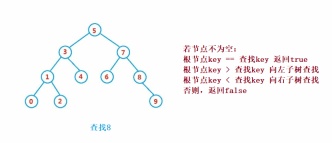
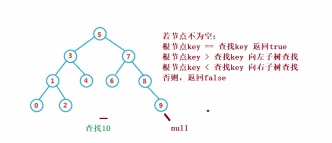
②Operation- Search
Binary search tree search is similar to binary search
 ##
##
public Node search(int key) {
Node cur = root;
while (cur != null) {
if(cur.val == key) {
return cur;
}else if(cur.val < key) {
cur = cur.right;
}else {
cur = cur.left;
}
}
return null;
}③Operation-Insert
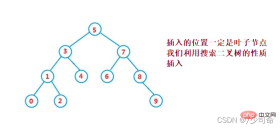
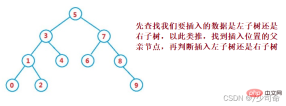
#
public boolean insert(int key) {
Node node = new Node(key);
if(root == null) {
root = node;
return true;
}
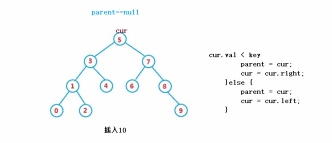
Node cur = root;
Node parent = null;
while(cur != null) {
if(cur.val == key) {
return false;
}else if(cur.val < key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
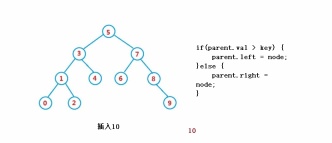
//parent
if(parent.val > key) {
parent.left = node;
}else {
parent.right = node;
}
return true;
} ④ Operation - Delete
④ Operation - Delete
The deletion operation is relatively complicated, but it is relatively easy to understand its principle
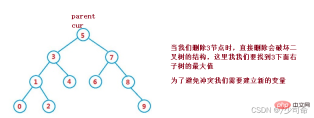
Suppose the node to be deleted is cur, and the parent node of the node to be deleted is parent
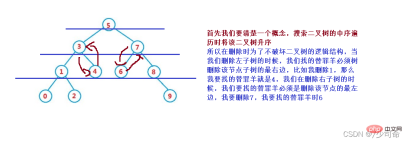
1. cur.left == null
1. cur is root, then root = cur.right
2. cur is not root, cur is parent.left, then parent.left = cur.right
3. cur is not root, cur is parent.right, then parent.right = cur.right
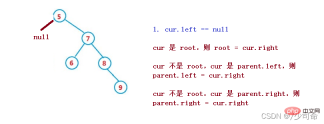
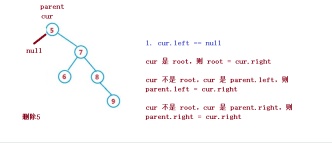
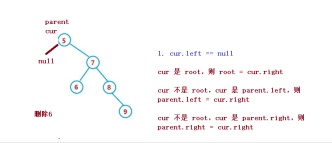
##2. cur.right == null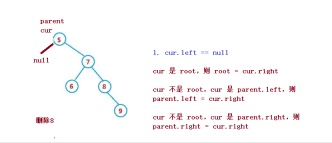
 ##
##
public void remove(Node parent,Node cur) {
if(cur.left == null) {
if(cur == root) {
root = cur.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if(cur.right == null) {
if(cur == root) {
root = cur.left;
}else if(cur == parent.left) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}else {
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(target == targetParent.left) {
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}
}
}
public void removeKey(int key) {
if(root == null) {
return;
}
Node cur = root;
Node parent = null;
while (cur != null) {
if(cur.val == key) {
remove(parent,cur);
return;
}else if(cur.val < key){
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
}⑤Performance Analysis 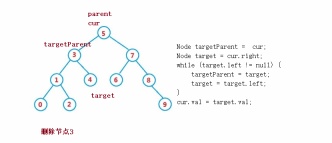 Both insertion and deletion operations must be searched first. Search efficiency represents the performance of each operation in the binary search tree.
Both insertion and deletion operations must be searched first. Search efficiency represents the performance of each operation in the binary search tree.
For a binary search tree with n nodes, if the probability of searching for each element is equal, the average search length of the binary search tree is a function of the depth of the node in the binary search tree, that is, the node The deeper the point, the more comparisons are made.
But for the same key code set, if the key codes are inserted in a different order, binary search trees with different structures may be obtained:
In the optimal case, the binary search tree is complete For a binary tree, the average number of comparisons is:
In the worst case, the binary search tree degenerates into a single branch tree, and the average number of comparisons is: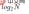
⑥完整代码
public class TextDemo {
public static class Node {
public int val;
public Node left;
public Node right;
public Node (int val) {
this.val = val;
}
}
public Node root;
/**
* 查找
* @param key
*/
public Node search(int key) {
Node cur = root;
while (cur != null) {
if(cur.val == key) {
return cur;
}else if(cur.val < key) {
cur = cur.right;
}else {
cur = cur.left;
}
}
return null;
}
/**
*
* @param key
* @return
*/
public boolean insert(int key) {
Node node = new Node(key);
if(root == null) {
root = node;
return true;
}
Node cur = root;
Node parent = null;
while(cur != null) {
if(cur.val == key) {
return false;
}else if(cur.val < key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
//parent
if(parent.val > key) {
parent.left = node;
}else {
parent.right = node;
}
return true;
}
public void remove(Node parent,Node cur) {
if(cur.left == null) {
if(cur == root) {
root = cur.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if(cur.right == null) {
if(cur == root) {
root = cur.left;
}else if(cur == parent.left) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}else {
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(target == targetParent.left) {
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}
}
}
public void removeKey(int key) {
if(root == null) {
return;
}
Node cur = root;
Node parent = null;
while (cur != null) {
if(cur.val == key) {
remove(parent,cur);
return;
}else if(cur.val < key){
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
}
}The above is the detailed content of Detailed explanation of examples of adding, inserting, deleting and creating Java binary search trees. For more information, please follow other related articles on the PHP Chinese website!
 带你搞懂Java结构化数据处理开源库SPLMay 24, 2022 pm 01:34 PM
带你搞懂Java结构化数据处理开源库SPLMay 24, 2022 pm 01:34 PM本篇文章给大家带来了关于java的相关知识,其中主要介绍了关于结构化数据处理开源库SPL的相关问题,下面就一起来看一下java下理想的结构化数据处理类库,希望对大家有帮助。
 Java集合框架之PriorityQueue优先级队列Jun 09, 2022 am 11:47 AM
Java集合框架之PriorityQueue优先级队列Jun 09, 2022 am 11:47 AM本篇文章给大家带来了关于java的相关知识,其中主要介绍了关于PriorityQueue优先级队列的相关知识,Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列,PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的,下面一起来看一下,希望对大家有帮助。
 完全掌握Java锁(图文解析)Jun 14, 2022 am 11:47 AM
完全掌握Java锁(图文解析)Jun 14, 2022 am 11:47 AM本篇文章给大家带来了关于java的相关知识,其中主要介绍了关于java锁的相关问题,包括了独占锁、悲观锁、乐观锁、共享锁等等内容,下面一起来看一下,希望对大家有帮助。
 一起聊聊Java多线程之线程安全问题Apr 21, 2022 pm 06:17 PM
一起聊聊Java多线程之线程安全问题Apr 21, 2022 pm 06:17 PM本篇文章给大家带来了关于java的相关知识,其中主要介绍了关于多线程的相关问题,包括了线程安装、线程加锁与线程不安全的原因、线程安全的标准类等等内容,希望对大家有帮助。
 详细解析Java的this和super关键字Apr 30, 2022 am 09:00 AM
详细解析Java的this和super关键字Apr 30, 2022 am 09:00 AM本篇文章给大家带来了关于Java的相关知识,其中主要介绍了关于关键字中this和super的相关问题,以及他们的一些区别,下面一起来看一下,希望对大家有帮助。
 Java基础归纳之枚举May 26, 2022 am 11:50 AM
Java基础归纳之枚举May 26, 2022 am 11:50 AM本篇文章给大家带来了关于java的相关知识,其中主要介绍了关于枚举的相关问题,包括了枚举的基本操作、集合类对枚举的支持等等内容,下面一起来看一下,希望对大家有帮助。
 java中封装是什么May 16, 2019 pm 06:08 PM
java中封装是什么May 16, 2019 pm 06:08 PM封装是一种信息隐藏技术,是指一种将抽象性函式接口的实现细节部分包装、隐藏起来的方法;封装可以被认为是一个保护屏障,防止指定类的代码和数据被外部类定义的代码随机访问。封装可以通过关键字private,protected和public实现。
 归纳整理JAVA装饰器模式(实例详解)May 05, 2022 pm 06:48 PM
归纳整理JAVA装饰器模式(实例详解)May 05, 2022 pm 06:48 PM本篇文章给大家带来了关于java的相关知识,其中主要介绍了关于设计模式的相关问题,主要将装饰器模式的相关内容,指在不改变现有对象结构的情况下,动态地给该对象增加一些职责的模式,希望对大家有帮助。


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

Atom editor mac version download
The most popular open source editor






