Detailed explanation of examples of adding, inserting, deleting and creating Java binary search trees

①Concept

Binary search tree is also called binary sorting tree. It is either an empty tree** or has the following properties Binary tree:

If its left subtree is not empty, then the values ​​of all nodes on the left subtree are less than the value of the root node

If its right subtree is not empty, then The values ​​of all nodes on the right subtree are greater than the value of the root node

Its left and right subtrees are also binary search trees

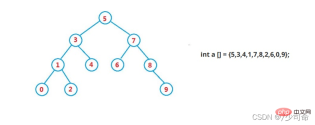
②Operation- Search

Binary search tree search is similar to binary search

##

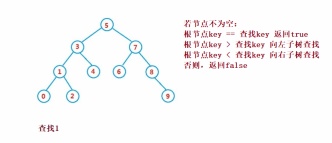
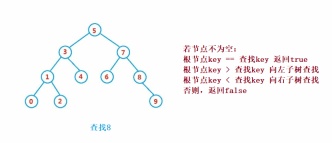
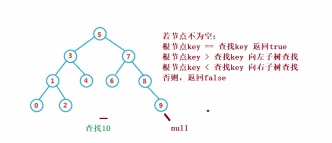public Node search(int key) {
        Node cur = root;
        while (cur != null) {
            if(cur.val == key) {
                return cur;
            }else if(cur.val < key) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }

③Operation-Insert

#

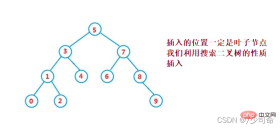
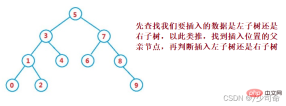
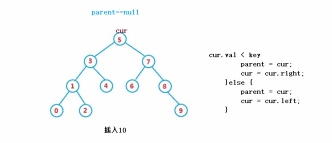
  public boolean insert(int key) {
        Node node = new Node(key);
        if(root == null) {
            root = node;
            return true;
        }
 
        Node cur = root;
        Node parent = null;
 
        while(cur != null) {
            if(cur.val == key) {
                return false;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //parent
        if(parent.val > key) {
            parent.left = node;
        }else {
            parent.right = node;
        }
 
        return true;
    }

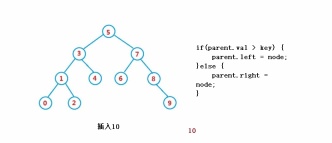④ Operation - Delete

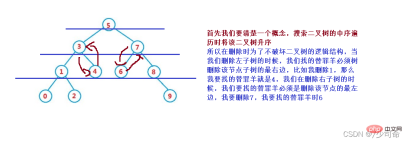
The deletion operation is relatively complicated, but it is relatively easy to understand its principle

Suppose the node to be deleted is cur, and the parent node of the node to be deleted is parent

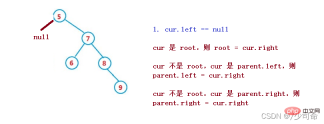
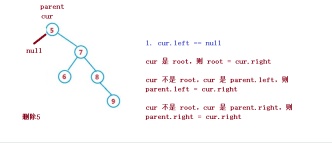
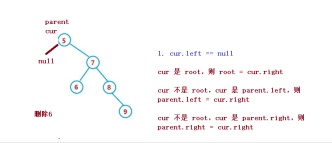
1. cur.left == null

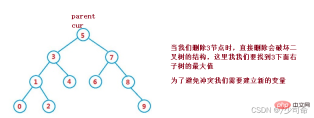
1. cur is root, then root = cur.right

2. cur is not root, cur is parent.left, then parent.left = cur.right

3. cur is not root, cur is parent.right, then parent.right = cur.right

##2. cur.right == null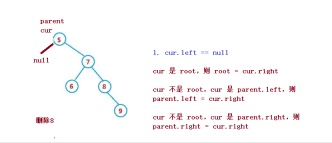

1. cur is root, then root = cur.left

2. Cur is not root, cur is parent.left, then parent.left = cur.left

3. Cur is not root, cur is parent.right, then parent.right = cur.left

The second case is the same as the first case, except in the opposite direction, no more drawing here

3. cur.left != null && cur.right != null

You need to use the replacement method to delete, that is, find the first node in the middle order (the smallest key code) in its right subtree, fill it with its value into the deleted node, and then process the node Deletion problem

When we delete when the left and right subtrees are both empty, deleting the node will destroy the structure of the tree, so we use the scapegoat method to solve it. The actual deletion process is still the above two. In this case, the properties of searching binary trees are still used here

##

public void remove(Node parent,Node cur) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node targetParent =  cur;
            Node target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }
 
  public void removeKey(int key) {
        if(root == null) {
            return;
        }
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                remove(parent,cur);
                return;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }

⑤Performance Analysis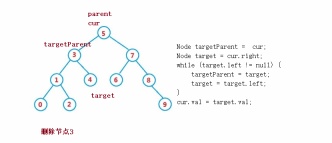

Both insertion and deletion operations must be searched first. Search efficiency represents the performance of each operation in the binary search tree.

For a binary search tree with n nodes, if the probability of searching for each element is equal, the average search length of the binary search tree is a function of the depth of the node in the binary search tree, that is, the node The deeper the point, the more comparisons are made.

But for the same key code set, if the key codes are inserted in a different order, binary search trees with different structures may be obtained:

In the optimal case, the binary search tree is complete For a binary tree, the average number of comparisons is:

In the worst case, the binary search tree degenerates into a single branch tree, and the average number of comparisons is: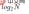

⑥完整代码

public class TextDemo {
 
    public static class Node {
        public int val;
        public Node left;
        public Node right;
 
        public Node (int val) {
            this.val = val;
        }
    }
 
 
    public Node root;
 
    /**
     * 查找
     * @param key
     */
    public Node search(int key) {
        Node cur = root;
        while (cur != null) {
            if(cur.val == key) {
                return cur;
            }else if(cur.val < key) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }
 
    /**
     *
     * @param key
     * @return
     */
    public boolean insert(int key) {
        Node node = new Node(key);
        if(root == null) {
            root = node;
            return true;
        }
 
        Node cur = root;
        Node parent = null;
 
        while(cur != null) {
            if(cur.val == key) {
                return false;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //parent
        if(parent.val > key) {
            parent.left = node;
        }else {
            parent.right = node;
        }
 
        return true;
    }
 
    public void remove(Node parent,Node cur) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node targetParent =  cur;
            Node target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }
 
    public void removeKey(int key) {
        if(root == null) {
            return;
        }
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                remove(parent,cur);
                return;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }
 
}

The above is the detailed content of Detailed explanation of examples of adding, inserting, deleting and creating Java binary search trees. For more information, please follow other related articles on the PHP Chinese website!