Home >Java >javaTutorial >How to implement Bloom filter in Java
How to implement Bloom filter in Java
- 王林forward
- 2023-04-24 21:43:191783browse
BitMap
Modern computers use binary (bit, bit) as the basic unit of information. 1 byte is equal to 8 bits. For example, bigA string is composed of 3 bytes , but it is actually expressed in binary when stored in the computer. The ASCII codes corresponding to big are 98, 105, and 103 respectively, and the corresponding binary numbers are 01100010, 01101001, and 01100111 respectively.
Many development languages provide the function of operating bits. Proper use of bits can effectively improve memory usage and development efficiency.
The basic idea of Bit-map is to use a bit to mark the value corresponding to an element, and the key is the element. Since data is stored in bit units, storage space can be greatly saved.
In Java, int occupies 4 bytes, 1 byte = 8 bits (1 byte = 8 bit), if we use the value of each of these 32 bits to represent a number, it is Otherwise, it can represent 32 numbers, which means that 32 numbers only need the space occupied by an int, which can reduce the space by 32 times.
1 Byte = 8 Bit, 1 KB = 1024 Byte, 1 MB = 1024 KB, 1GB = 1024 MB
Assume that the website has 100 million users who visit independently every day There are 50 million users. If you use the collection type and BitMap to store active users every day:
1. If the user ID is int type, 4 bytes, 32 bits, the collection type occupies 50,000 spaces. 000 * 4/1024/1024 = 200M;
2. If stored in bits, 50 million numbers are 50 million bits, and the occupied space is 50 000 000/8/1024/1024 = 6M.
So how to use BitMap to represent a number?
As mentioned above, bit bits are used to mark the value corresponding to an element, and the key is the element. We can imagine BitMap as an array in units of bits. The array Each unit can only store 0 and 1 (0 means the number does not exist, 1 means it exists), and the subscript of the array is called the offset in BitMap. For example, we need to represent the four numbers {1,3,5,7} as follows:
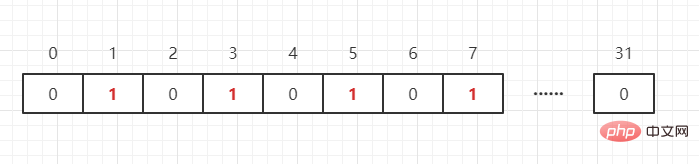
What if there is another number 65? You only need to open int[N/32 1] int arrays to store these data (where N represents the maximum value in this group of data), that is:
int [0]: Can represent 0~31
int[1]: Can represent 32~63
int[2] : Can represent 64~95
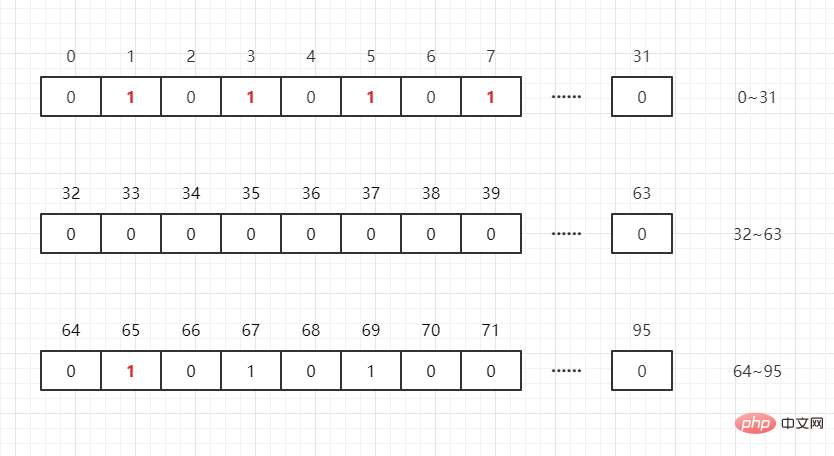
Suppose we want to determine whether any integer is in the list, then M/32 will get the subscript, M2 will know where it is in this subscript, such as:
65/32 = 2, 652=1, that is, 65 is in The 1st bit in int[2].
Bloom filter
Essentially, Bloom filter is a data structure, a relatively clever probabilistic data structure, characterized by efficient insertion and query, which can be used to tell you " Something must not exist or may exist”.
Compared with traditional data structures such as List, Set, Map, etc., it is more efficient and takes up less space, but the disadvantage is that the results it returns are probabilistic, not exact.
In fact, Bloom filters are widely used in webpage blacklist system, spam filtering system,crawler URL weight judgment system, etc. , Google's famous distributed database Bigtable uses Bloom filters to find non-existent rows or columns to reduce the number of IO disk searches. Google Chrome browser uses Bloom filters to accelerate safe browsing services.
Bloom filters are also used in many Key-Value systems to speed up the query process, such as Hbase, Accumulo, Leveldb. Generally speaking, Value is saved in the disk, and accessing the disk takes a lot of time. However, Bloom filters can be used to quickly determine whether the Value corresponding to a Key exists, so many unnecessary disk IO operations can be avoided.
Map an element into a point in a bit array (Bit Array) through a Hash function. In this way, we only need to see if the point is 1 to know whether it is in the set. This is the basic idea of Bloom filter.
Application Scenario
1. There are currently 1 billion natural numbers, arranged in disorder, and they need to be sorted. The restrictions are implemented on 32-bit machines, and the memory limit is 2G. How is it done?
2. How to quickly locate whether the URL address is in the blacklist? (Each URL averages 64 bytes)
3. Do you need to analyze user login behavior to determine user activity?
4. Web crawler-how to determine whether a URL has been crawled?
5. Quickly locate user attributes (blacklist, whitelist, etc.)?
6. Data is stored on disk, how to avoid a large number of invalid IO?
7. Determine whether an element exists in billions of data?
8. Cache penetration.
Disadvantages of traditional data structures
Generally speaking, it is OK to store the web page URL in the database for search, or to create a hash table for search.
When the amount of data is small, it is right to think like this. The value can indeed be mapped to the key of HashMap, and then the result can be returned within O(1) time complexity, which is extremely efficient. However, the implementation of HashMap also has shortcomings, such as a high proportion of storage capacity. Considering the existence of load factors, usually the space cannot be fully used. For example, if a 10 million HashMap, Key=String (length does not exceed 16 characters, and Very little repeatability), Value=Integer, how much space will it occupy? 1.2G.
In fact, using bitmap, 10 million int types only require about 40M (10 000 000 * 4/1024/1024 =40M) space, accounting for 3%. 10 million Integer requires about 161M space. , accounting for 13.3%.
It can be seen that once you have a lot of values, such as hundreds of millions, the memory size occupied by HashMap can be imagined.
But if the entire webpage blacklist system contains 10 billion webpage URLs, searching in the database is very time-consuming, and if each URL space is 64B, then 640GB of memory is required, which is difficult for ordinary servers to achieve. need.
Implementation Principle
Suppose we have a set A, and there are n elements in A. Use k hash hash functions to map each element in A to different positions in an array B with a length of a bit. The binary numbers at these positions Both are set to 1. If the element to be checked is mapped by these k hash functions and it is found that the binary numbers at its k positions are all 1, this element is likely to belong to set A. Otherwise, must not belong to the set A.
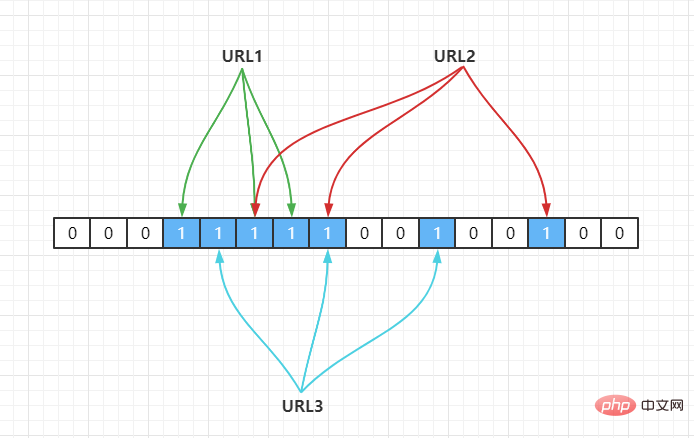
For example, we have 3 URLs{URL1,URL2,URL3}, and map them to an array of length 16 through a hash function, as follows:
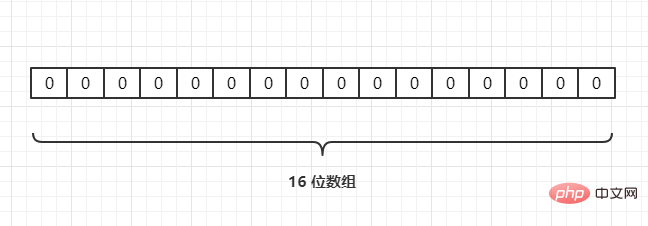
Hash2(), it is mapped to the array through hash operation, assuming Hash2(URL1) = 3, Hash2(URL2) = 6, Hash2(URL3) = 6, as follows:
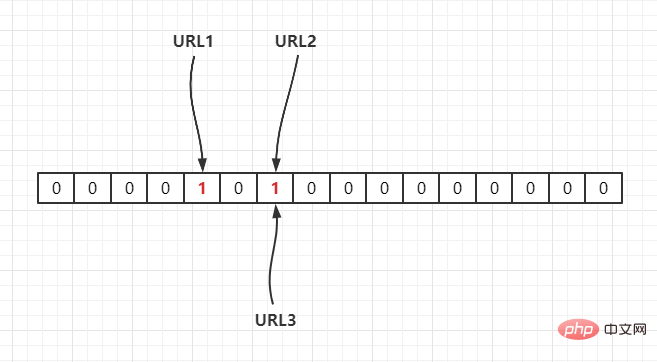
Whether URL1 is in this set, calculate its subscript through Hash(1), and get its value. If it is 1, it means it exists.
URL2, URL3 are all located at the same position. Assuming that the Hash function is good, if the length of our array is m points, then if We want to reduce the conflict rate to, for example, 1%. This hash table can only accommodate m/100 elements. Obviously, the space utilization rate becomes low, which means it cannot be done. To space effective (space-efficient).
Hash2(URL1) = 3,Hash3(URL1) = 5,Hash4(URL1) = 6 Hash2(URL2) = 5,Hash3(URL2) = 8,Hash4(URL2) = 14 Hash2(URL3) = 4,Hash3(URL3) = 7,Hash4(URL3) = 10
URL1000 comes at this time. After hash calculation, it is found that the bits are as follows:
Hash2(URL1000) = 7,Hash3(URL1000) = 8,Hash4(URL1000) = 14
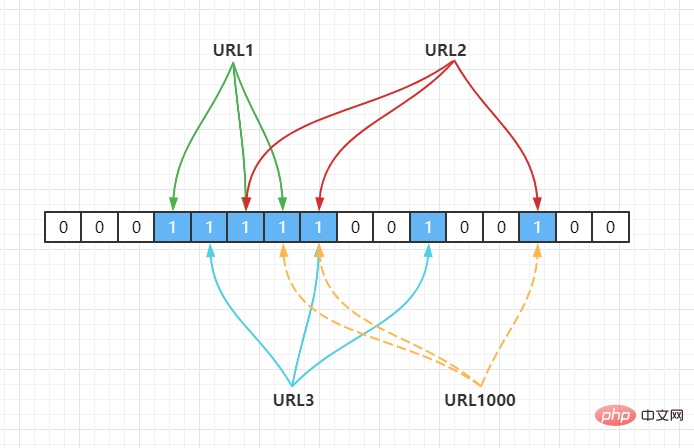
URL1, URL2, URL3. At this time, the program will determine that the URL1000 value exists.
What the Bloom filter judges to exist may not exist, but what is judged to not exist must not exist.
Bloom filter can accurately represent a set and accurately determine whether an element is in this set. The accuracy is determined by the user's specific design. It is impossible to achieve 100% accuracy. . But the advantage of the Bloom filter is that it can achieve a higher accuracyusing very little space. Implementation
Redis’ bitmap
It is executed based on the relevant instructions of redis’ bitmap data structure.
RedisBloom
Bloom filters can be implemented using bitmap operations in Redis. It was not until the Redis 4.0 version provided the plug-in function that the Bloom filters officially provided by Redis were officially On the scene, the Bloom filter is loaded into the Redis Server as a plug-in. The official website recommends a RedisBloom as the Module of the Redis Bloom filter.
Guava’s BloomFilter
When the Guava project released version 11.0, one of the newly added features was the BloomFilter class.
Redisson
Redisson implements a Bloom filter based on bitmap.
public static void main(String[] args) {
Config config = new Config();
// 单机环境
config.useSingleServer().setAddress("redis://192.168.153.128:6379");
//构造Redisson
RedissonClient redisson = Redisson.create(config);
RBloomFilter<String> bloomFilter = redisson.getBloomFilter("nameList");
//初始化布隆过滤器:预计元素为100000000L,误差率为3%,根据这两个参数会计算出底层的 bit 数组大小
bloomFilter.tryInit(100000L, 0.03);
//将 10086 插入到布隆过滤器中
bloomFilter.add("10086");
//判断下面号码是否在布隆过滤器中
System.out.println(bloomFilter.contains("10086"));//true
System.out.println(bloomFilter.contains("10010"));//false
System.out.println(bloomFilter.contains("10000"));//false
}解决缓存穿透
缓存穿透是指查询一个根本不存在的数据,缓存层和存储层都不会命中,如果从存储层查不到数据则不写入缓存层。
缓存穿透将导致不存在的数据每次请求都要到存储层去查询,失去了缓存保护后端存储的意义。缓存穿透问题可能会使后端存储负载加大,由于很多后端存储不具备高并发性,甚至可能造成后端存储宕掉。
因此我们可以用布隆过滤器来解决,在访问缓存层和存储层之前,将存在的 key 用布隆过滤器提前保存起来,做第一层拦截。
例如:一个推荐系统有 4 亿个用户 id,每个小时算法工程师会根据每个用户之前历史行为计算出推荐数据放到存储层中,但是最新的用户由于没有历史行为,就会发生缓存穿透的行为,为此可以将所有推荐数据的用户做成布隆过滤器。如果布隆过滤器认为该用户 id 不存在,那么就不会访问存储层,在一定程度保护了存储层。
注:布隆过滤器可能会误判,放过部分请求,当不影响整体,所以目前该方案是处理此类问题最佳方案
The above is the detailed content of How to implement Bloom filter in Java. For more information, please follow other related articles on the PHP Chinese website!

