What are the recursive and non-recursive traversal methods of Java binary tree?

Preface

The traversal methods of binary trees are divided into pre-order traversal, in-order traversal, subsequent traversal and level-order traversal.

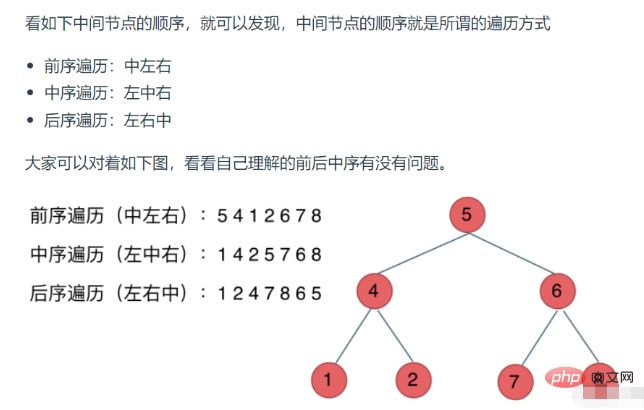
1. Recursive traversal

For recursion, we have to talk about the three elements of recursion: preorder traversal as an example

Recursive parameter entry Parameters and return values

Because we want to print out the value of the node traversed in preorder, we need to pass in the value of the node in the List in the parameter. Apart from this, there is no need to process any data and there is no need to have a return value. , so the return type of the recursive function is void, the code is as follows:

public void preorder(TreeNode root, List<Integer> result)

Determine the termination condition

In the process of recursion, how to count the end of the recursion? Of course, the currently traversed node is empty , then this level of recursion is about to end, so if the currently traversed node is empty, just return directly

if (root == null) return;

Single-layer loop logic

Preorder traversal is the middle and left order, Therefore, the logic of single-level recursion is to first take the value of the middle node. The code is as follows:

result.add(root.val);
preorder(root.left, result);
preorder(root.right, result);

// 前序遍历·递归·LC144_二叉树的前序遍历
class Solution {
    public List preorderTraversal(TreeNode root) {
        List result = new ArrayList();
        preorder(root, result);
        return result;
    }
    public void preorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        result.add(root.val);//先保存中间节点
        preorder(root.left, result); //处理左边节点
        preorder(root.right, result); //处理右边节点
    }
}
// 中序遍历·递归·LC94_二叉树的中序遍历
class Solution {
    public List inorderTraversal(TreeNode root) {
        List res = new ArrayList<>();
        inorder(root, res);
        return res;
    }
    void inorder(TreeNode root, List list) {
        if (root == null) {
            return;
        }
        inorder(root.left, list); //先处理左边节点
        list.add(root.val);       //保存中间当前的节点
        inorder(root.right, list);//先处理右边节点
    }
}
// 后序遍历·递归·LC145_二叉树的后序遍历
class Solution {
    public List postorderTraversal(TreeNode root) {
        List res = new ArrayList<>();
        postorder(root, res);
        return res;
    }
    void postorder(TreeNode root, List list) {
        if (root == null) {
            return;
        }
        postorder(root.left, list);  //先处理左边节点
        postorder(root.right, list); //再处理右边节点
        list.add(root.val);          //保存最后  
    }
}

2. Non-iterative traversal

//前序遍历
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack = new Stack();
        if (root == null) return res;
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            res.add(node.val);
            if (node.right != null) { //先将右孩子入栈，因为它在最后
                stack.push(node.right);
            }
            if (node.left != null) { //左孩子入栈再出栈
                stack.push(node.left);
            }
        }
        return res;
    }
}
//中序遍历
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) return res;
        Stack<TreeNode> stack = new Stack();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {
            //如果可以，一直往左下探
            if (cur != null) {
                stack.push(cur);
                cur = cur.left;
            } else {
                cur = stack.pop(); //弹出来的肯定是叶子节点或中间节点
                res.add(cur.val); //将这个节点加入list
                cur = cur.right; //查看当前节点是否有右节点，如果右，肯定是中间节点，如果没有，就是叶子节点，继续弹出就可以
            }
        }
        return res;
    }
}
//后序遍历
//再来看后序遍历，先序遍历是中左右，后续遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后在反转result数组，输出的结果顺序就是左右中
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) return res;
        Stack<TreeNode> stack = new Stack();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            res.add(node.val);
            if (node.left != null) stack.push(node.left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
            if (node.right != null) stack.push(node.right);// 空节点不入栈 
        }
        Collections.reverse(res); // 将结果反转之后就是左右中的顺序了
        return res;
    }
}

3. Unified iteration method of binary tree

//前序遍历
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        Stack<TreeNode> st = new Stack<>();
        if (root != null) st.push(root);
        while (!st.empty()) {
            TreeNode node = st.peek();
            if (node != null) {
                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）
                if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）
                st.push(node);                          // 添加中节点
                st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。
            } else { // 只有遇到空节点的时候，才将下一个节点放进结果集
                st.pop();           // 将空节点弹出
                node = st.peek();    // 重新取出栈中元素
                st.pop();
                result.add(node.val); // 加入到结果集
            }
        }
        return result;
    }
}
//中序遍历
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        Stack<TreeNode> st = new Stack<>();
        if (root != null) st.push(root);
        while (!st.empty()) {
            TreeNode node = st.peek();
            if (node != null) {
                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）
                st.push(node);                          // 添加中节点
                st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。
                if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）
            } else { // 只有遇到空节点的时候，才将下一个节点放进结果集
                st.pop();           // 将空节点弹出
                node = st.peek();    // 重新取出栈中元素
                st.pop();
                result.add(node.val); // 加入到结果集
            }
        }
        return result;
    }
}
//后序遍历
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        Stack<TreeNode> st = new Stack<>();
        if (root != null) st.push(root);
        while (!st.empty()) {
            TreeNode node = st.peek();
            if (node != null) {
                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                st.push(node);                          // 添加中节点
                st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。
                if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）
                if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）         
            } else { // 只有遇到空节点的时候，才将下一个节点放进结果集
                st.pop();           // 将空节点弹出
                node = st.peek();    // 重新取出栈中元素
                st.pop();
                result.add(node.val); // 加入到结果集
            }
        }
        return result;
    }
}

The above is the detailed content of What are the recursive and non-recursive traversal methods of Java binary tree?. For more information, please follow other related articles on the PHP Chinese website!