 Technology peripherals
Technology peripherals AI
AI Compare time series forecasting methods based on SARIMA, XGBoost and CNN-LSTM.
Compare time series forecasting methods based on SARIMA, XGBoost and CNN-LSTM.Performance Testing and Comparison of Analyzing and Predicting Solar Power Generation Using Statistical Testing and Machine Learning
This article will discuss techniques for obtaining tangible value from data sets through the use of hypothesis testing, feature engineering, time series modeling methods, etc. . I will also address issues such as data leakage and data preparation for different time series models, and conduct comparative testing of three common time series forecasts.
Introduction
Time series prediction is a frequently studied topic. Here we use the data of two solar power plants to study its laws and conduct modeling. Address these issues by first boiling them down into two questions:
- Is it possible to identify underperforming solar modules?
- Is it possible to predict the solar power generation for two days?
Before we continue to answer these questions, let us first understand how solar power plants generate electricity.

The above diagram describes the generation process from solar panel modules to the grid. Solar energy is directly converted into electrical energy through the photoelectric effect. When materials such as silicon (the most common semiconductor material in solar panels) are exposed to light, photons (subatomic particles of electromagnetic energy) are absorbed and free electrons are released, creating direct current (DC). Using an inverter, DC power is converted into alternating current (AC) and sent to the grid, where it can be distributed to homes.
Data
The raw data consists of two comma-separated value (CSV) files for each solar power plant. One document shows the power generation process and the other shows the measurements recorded by the solar farm's sensors. The two datasets for each solar power plant were organized into a pandas df.
Data from Solar Power Plant 1 (SP1) and Solar Power Plant 2 (SP2) were collected every 15 minutes from May 15, 2020 to June 18, 2020. Both SP1 and SP2 datasets contain the same variables.
- Date Time - an interval of 15 minutes
- Ambient temperature - the temperature of the air around the module
- Module temperature - the temperature of the module
- Irradiation—— Radiation on the module
- DC Power (kW) -Direct current
- AC Power (kW) -AC
- Daily Yield-Total daily power generation
- Total Yield - the cumulative yield of the inverter
- Plant ID - the unique identification of the solar power plant
- Module ID - the unique identification of each module
For weather sensors To record the ambient temperature, module temperature and radiation of each solar power plant.
For this data set DC power will be the dependent variable (target variable). Our goal is to try to find underperforming solar modules.
Two independent dfs are used for analysis and prediction. The only difference is that the data used for forecasting is resampled to hourly intervals, while the data frame used for analysis contains 15-minute intervals.
First we remove the Plant ID as it adds no value to trying to answer the above question. Module IDs are also removed from the prediction dataset. Tables 1 and 2 show data examples.


Before continuing to analyze the data, we made some assumptions about the solar power plant, including:
- Data acquisition instrument is fault-free
- The module is cleaned regularly (ignoring the impact of maintenance)
- There are no occlusion problems around the two solar power plants
Exploratory data analysis ( EDA)
For those new to data science, EDA is a critical step in understanding data by plotting visualizations and performing statistical tests. We can first observe the performance of each solar power plant by plotting DC and AC for SP1 and SP2.

SP1 shows an order of magnitude higher DC power than sp2. Assuming that the data collected by SP1 is correct and the instrument used to record the data is not faulty, this means that the inverter in SP1 needs more in-depth research.

By pressing each The daily frequency aggregate AC and DC power of each module, Figure 3 shows the inverter efficiency of all modules in SP1. According to knowledge in the field, the efficiency of solar inverters should be between 93-96%. Since the efficiency of all modules ranges from 9.76% - 9.79%, this illustrates the need to investigate the performance of the inverter and whether it needs to be replaced.
Since SP1 showed problems with the inverter, further analysis was only done on SP2.
Although this short analysis is the result of more time spent studying the inverter, it does not answer the main question of determining solar module performance.
Because the SP2's inverter is functioning properly, any anomalies can be identified and investigated by digging deeper into the data.
Figure 4 shows the relationship between module temperature and ambient temperature, and there are cases where the module temperature is extremely high.

This seems to go against our knowledge, but it can be seen that high temperature does have a negative impact on solar panels. When photons come into contact with electrons within a solar cell, they release free electrons, but at higher temperatures, more electrons are already in an excited state, which reduces the voltage the panels can produce, thereby reducing efficiency.
With this phenomenon in mind, Figure 5 below shows the module temperature and DC power for SP2 (data points where the ambient temperature is lower than the module temperature and times of day when the module is running with a lower number have been filtered, to prevent data skew).

In Figure 5, the red line represents the average temperature. You can see here that there is a clear tipping point and signs of DC power stagnation. Starts plateauing at ~52°C. In order to find solar modules with suboptimal performance, all rows showing module temperatures exceeding 52°C were removed.
Figure 6 below shows the DC power of each module in SP2 over the course of a day. This basically meets the expectations, and the power generation is larger at noon. But there is another problem. During peak operating periods, the power generation is low. It is difficult for us to summarize the reasons for this situation, because the weather conditions may be poor that day, or the SP2 may need routine maintenance, etc.
There are also signs of low-performance modules in Figure 6. They can be identified as modules (individual data points) on the graph that deviate from the nearest cluster.

To determine which modules are performing poorly, we can perform statistical tests while comparing the performance of each module to other modules to determine performance.
Every 15 minutes, the distribution of DC power supplies of different modules at the same time is a normal distribution. Through hypothesis testing, it can be determined which modules perform poorly. Counts are the number of times a module falls outside the 99.9% confidence interval with a p-value
Figure 7 shows, in descending order, the number of times each module was statistically significantly lower than other modules during the same period.

It is clear from Figure 7 that the module 'Quc1TzYxW2pYoWX' is problematic. This information can be provided to relevant SP2 staff to investigate the cause.
Modeling
Below we start using three different time series algorithms: SARIMA, XGBoost and CNN-LSTM to model and compare
For all three models , both use predicting the next data point for prediction. Walk-forward validation is a technique used in time series modeling because predictions become less accurate over time, so a more practical approach is to retrain the model with actual data when it becomes available.
The data needs to be studied in more detail before modeling. Figure 8 shows the correlation heatmap for all features in the SP2 dataset. The heat map shows the strong correlation of the dependent variable, DC power, with module temperature, irradiation and ambient temperature. These characteristics may play an important role in prediction.
In the heat map below, AC power shows a Pearson correlation coefficient of 1. To prevent data leakage issues, we remove DC power from the data.

SARIMA
Seasonal Autoregressive Integrated Moving Average (SARIMA) is a univariate time series forecasting method. Since the target variable shows signs of a 24-hour cyclic period, SARIMA is an efficient modeling option as it takes seasonal effects into account. This can be observed in the seasonal breakdown chart below.

#The SARIMA algorithm requires the data to be stationary. There are various ways to test whether data are stationary, such as statistical tests (augmented Dickey-Fowler test), summary statistics (comparing means/variances of different parts of the data) and visually analyzing the data. It is important to conduct multiple tests before modeling.
The Augmented Dickey-Fuller (ADF) test is a "unit root test" used to determine whether a time series is stationary. Basically, it is a statistical significance test where there is a null hypothesis and an alternative hypothesis and a conclusion is drawn based on the resulting p-value.
Null hypothesis: Time series data is non-stationary.
Alternative hypothesis: The time series data are stationary.
In our example, if the p-value ≤ 0.05, we can reject the null hypothesis and confirm that the data has no unit root.
from statsmodels.tsa.stattools import adfuller
result = adfuller(plant2_dcpower.values)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
print('t%s: %.3f' % (key, value))
From the ADF test, the p value is 0.000553,
In order to use SARIMA to model the dependent variable, the time series needs to be stationary. As shown in Figure 9 (first and third graphs), DC power has clear signs of seasonality. Take the first difference [t-(t-1)] to remove the seasonal component, as shown in Figure 10, since it looks similar to a normal distribution. The data is now stationary and suitable for the SARIMA algorithm.

SARIMA’s hyperparameters include p (autoregressive order), d (difference order), q (moving average order), p (seasonal autoregressive order) ), d (order of seasonal differences), q (order of seasonal moving average), m (time step of seasonal cycle), trend (deterministic trend).

Figure 11 shows the autocorrelation (ACF), partial autocorrelation (PACF) and seasonal ACF/PACF plots. The ACF plot shows the correlation between a time series and its delayed version. PACF shows a direct correlation between a time series and its lagged version. The blue shaded area represents the confidence interval. SACF and SPACF can be calculated by taking the seasonal difference (m) from the original data, in this case 24 because there is an obvious 24-hour seasonal effect in the ACF plot.
According to our intuition, the starting point of the hyperparameters can be derived from the ACF and PACF graphs. For example, both ACF and PACF show a gradual downward trend, that is, the autoregressive order (p) and the moving average order (q) are both greater than 0. p and p can be determined by looking at the PCF and SPCF plots respectively, and counting the number of lags that become statistically significant before the lag value becomes insignificant. Likewise, q and q can be found in ACF and SACF diagrams.
The difference order (d) can be determined by the number of differences that make the data stationary. Seasonal difference order (D) is estimated from the number of differences required to remove the seasonal component from the time series.
You can read this article for these hyperparameter selections: https://arauto.readthedocs.io/en/latest/how_to_choose_terms.html
You can also use the grid search method for hyperparameter optimization , select the optimal hyperparameters based on the minimum mean square error (MSE), including p = 2, d = 0, q = 4, p = 2, d = 1, q = 6, m = 24, trend = ' n '( no trend).
from time import time
from sklearn.metrics import mean_squared_error
from statsmodels.tsa.statespace.sarimax import SARIMAX
configg = [(2, 1, 4), (2, 1, 6, 24), 'n']
def train_test_split(data, test_len=48):
"""
Split data into training and testing.
"""
train, test = data[:-test_len], data[-test_len:]
return train, test
def sarima_model(data, cfg, test_len, i):
"""
SARIMA model which outputs prediction and model.
"""
order, s_order, t = cfg[0], cfg[1], cfg[2]
model = SARIMAX(data, order=order, seasonal_order=s_order, trend=t,
enforce_stationarity=False, enfore_invertibility=False)
model_fit = model.fit(disp=False)
yhat = model_fit.predict(len(data))
if i + 1 == test_len:
return yhat, model_fit
else:
return yhat
def walk_forward_val(data, cfg):
"""
A walk forward validation technique used for time series data. Takes current value of x_test and predicts
value. x_test is then fed back into history for the next prediction.
"""
train, test = train_test_split(data)
pred = []
history = [i for i in train]
test_len = len(test)
for i in range(test_len):
if i + 1 == test_len:
yhat, s_model = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
mse = mean_squared_error(test, pred)
return pred, mse, s_model
else:
yhat = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
history.append(test[i])
pass
if __name__ == '__main__':
start_time = time()
sarima_pred_plant2, sarima_mse, s_model = walk_forward_val(plant2_dcpower, configg)
time_len = time() - start_time
print(f'SARIMA runtime: {round(time_len/60,2)} mins')
Figure 12 shows the comparison of the predicted values of the SARIMA model with the DC power recorded in SP2 during 2 days.
To analyze the performance of the model, Figure 13 shows the model diagnostics. The correlation plot shows almost no correlation after the first lag, and the histogram below shows a normal distribution around the mean of zero. From this we can say that the model cannot gather further information from the data.

XGBoost
XGBoost (eXtreme Gradient Boosting) is a gradient boosting decision tree algorithm. It uses an ensemble approach where new decision tree models are added to modify existing decision tree scores. Unlike SARIMA, XGBoost is a multivariate machine learning algorithm, which means that the model can adopt multiple features to improve model performance.
We use feature engineering to improve model accuracy. 3 additional characteristics were also created, which include lagging versions of the AC and DC power, S1_AC_POWER and S1_DC_POWER respectively, and the overall efficiency EFF, which is the AC power divided by the DC power. And remove AC_POWER and MODULE_TEMPERATURE from the data. Figure 14 shows the importance level of features by gain (average gain of splitting using a feature) and weight (number of times a feature appears in the tree).

Determine the hyperparameters used in modeling through grid search. The results are: *learning rate = 0.01, number of estimators = 1200, subsample = 0.8, colsample by tree = 1, colsample by level = 1, min child weight = 20 and max depth = 10
We use MinMaxScaler to scale the training data to between 0 and 1 (you can also experiment with other scalers such as log-transform and standard-scaler, which depends on the distribution of the data). Convert the data into a supervised learning dataset by moving all independent variables backward by a certain amount of time.
import numpy as np
import pandas as pd
import xgboost as xgb
from sklearn.preprocessing import MinMaxScaler
from time import time
def train_test_split(df, test_len=48):
"""
split data into training and testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
def data_to_supervised(df, shift_by=1, target_var='DC_POWER'):
"""
Convert data into a supervised learning problem.
"""
target = df[target_var][shift_by:].values
dep = df.drop(target_var, axis=1).shift(-shift_by).dropna().values
data = np.column_stack((dep, target))
return data
def xgb_forecast(train, x_test):
"""
XGBOOST model which outputs prediction and model.
"""
x_train, y_train = train[:,:-1], train[:,-1]
xgb_model = xgb.XGBRegressor(learning_rate=0.01, n_estimators=1500, subsample=0.8,
colsample_bytree=1, colsample_bylevel=1,
min_child_weight=20, max_depth=14, objective='reg:squarederror')
xgb_model.fit(x_train, y_train)
yhat = xgb_model.predict([x_test])
return yhat[0], xgb_model
def walk_forward_validation(df):
"""
A walk forward validation approach by scaling the data and changing into a supervised learning problem.
"""
preds = []
train, test = train_test_split(df)
scaler = MinMaxScaler(feature_range=(0,1))
train_scaled = scaler.fit_transform(train)
test_scaled = scaler.transform(test)
train_scaled_df = pd.DataFrame(train_scaled, columns = train.columns, index=train.index)
test_scaled_df = pd.DataFrame(test_scaled, columns = test.columns, index=test.index)
train_scaled_sup, test_scaled_sup = data_to_supervised(train_scaled_df), data_to_supervised(test_scaled_df)
history = np.array([x for x in train_scaled_sup])
for i in range(len(test_scaled_sup)):
test_x, test_y = test_scaled_sup[i][:-1], test_scaled_sup[i][-1]
yhat, xgb_model = xgb_forecast(history, test_x)
preds.append(yhat)
np.append(history,[test_scaled_sup[i]], axis=0)
pred_array = test_scaled_df.drop("DC_POWER", axis=1).to_numpy()
pred_num = np.array([pred])
pred_array = np.concatenate((pred_array, pred_num.T), axis=1)
result = scaler.inverse_transform(pred_array)
return result, test, xgb_model
if __name__ == '__main__':
start_time = time()
xgb_pred, actual, xgb_model = walk_forward_validation(dropped_df_cat)
time_len = time() - start_time
print(f'XGBOOST runtime: {round(time_len/60,2)} mins')图15显示了XGBoost模型的预测值与SP2 2天内记录的直流功率的比较。

CNN-LSTM
CNN-LSTM (convolutional Neural Network Long - Short-Term Memory)是两种神经网络模型的混合模型。CNN是一种前馈神经网络,在图像处理和自然语言处理方面表现出了良好的性能。它还可以有效地应用于时间序列数据的预测。LSTM是一种序列到序列的神经网络模型,旨在解决长期存在的梯度爆炸/消失问题,使用内部存储系统,允许它在输入序列上积累状态。
在本例中,使用CNN-LSTM作为编码器-解码器体系结构。由于CNN不直接支持序列输入,所以我们通过1D CNN读取序列输入并自动学习重要特征。然后LSTM进行解码。与XGBoost模型类似,使用scikitlearn的MinMaxScaler使用相同的数据并进行缩放,但范围在-1到1之间。对于CNN-LSTM,需要将数据重新整理为所需的结构:[samples, subsequences, timesteps, features],以便可以将其作为输入传递给模型。
由于我们希望为每个子序列重用相同的CNN模型,因此使用timedidistributedwrapper对每个输入子序列应用一次整个模型。在下面的图16中可以看到最终模型中使用的不同层的模型摘要。

在将数据分解为训练数据和测试数据之后,将训练数据分解为训练数据和验证数据集。在所有训练数据(包括验证数据)的每次迭代之后,模型可以进一步使用这一点来评估模型的性能。
学习曲线是深度学习中使用的一个很好的诊断工具,它显示了模型在每个阶段之后的表现。下面的图17显示了模型如何从数据中学习,并显示了验证数据与训练数据的收敛。这是良好模特训练的标志。

import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
import keras
from keras.models import Sequential
from keras.layers.convolutional import Conv1D, MaxPooling1D
from keras.layers import LSTM, TimeDistributed, RepeatVector, Dense, Flatten
from keras.optimizers import Adam
n_steps = 1
subseq = 1
def train_test_split(df, test_len=48):
"""
Split data in training and testing. Use 48 hours as testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
def split_data(sequences, n_steps):
"""
Preprocess data returning two arrays.
"""
x, y = [], []
for i in range(len(sequences)):
end_x = i + n_steps
if end_x > len(sequences):
break
x.append(sequences[i:end_x, :-1])
y.append(sequences[end_x-1, -1])
return np.array(x), np.array(y)
def CNN_LSTM(x, y, x_val, y_val):
"""
CNN-LSTM model.
"""
model = Sequential()
model.add(TimeDistributed(Conv1D(filters=14, kernel_size=1, activation="sigmoid",
input_shape=(None, x.shape[2], x.shape[3]))))
model.add(TimeDistributed(MaxPooling1D(pool_size=1)))
model.add(TimeDistributed(Flatten()))
model.add(LSTM(21, activation="tanh", return_sequences=True))
model.add(LSTM(14, activation="tanh", return_sequences=True))
model.add(LSTM(7, activation="tanh"))
model.add(Dense(3, activation="sigmoid"))
model.add(Dense(1))
model.compile(optimizer=Adam(learning_rate=0.001), loss="mse", metrics=['mse'])
history = model.fit(x, y, epochs=250, batch_size=36,
verbose=0, validation_data=(x_val, y_val))
return model, history
# split and resahpe data
train, test = train_test_split(dropped_df_cat)
train_x = train.drop(columns="DC_POWER", axis=1).to_numpy()
train_y = train["DC_POWER"].to_numpy().reshape(len(train), 1)
test_x = test.drop(columns="DC_POWER", axis=1).to_numpy()
test_y = test["DC_POWER"].to_numpy().reshape(len(test), 1)
#scale data
scaler_x = MinMaxScaler(feature_range=(-1,1))
scaler_y = MinMaxScaler(feature_range=(-1,1))
train_x = scaler_x.fit_transform(train_x)
train_y = scaler_y.fit_transform(train_y)
test_x = scaler_x.transform(test_x)
test_y = scaler_y.transform(test_y)
# shape data into CNN-LSTM format [samples, subsequences, timesteps, features] ORIGINAL
train_data_np = np.hstack((train_x, train_y))
x, y = split_data(train_data_np, n_steps)
x_subseq = x.reshape(x.shape[0], subseq, x.shape[1], x.shape[2])
# create validation set
x_val, y_val = x_subseq[-24:], y[-24:]
x_train, y_train = x_subseq[:-24], y[:-24]
n_features = x.shape[2]
actual = scaler_y.inverse_transform(test_y)
# run CNN-LSTM model
if __name__ == '__main__':
start_time = time()
model, history = CNN_LSTM(x_train, y_train, x_val, y_val)
prediction = []
for i in range(len(test_x)):
test_input = test_x[i].reshape(1, subseq, n_steps, n_features)
yhat = model.predict(test_input, verbose=0)
yhat_IT = scaler_y.inverse_transform(yhat)
prediction.append(yhat_IT[0][0])
time_len = time() - start_time
mse = mean_squared_error(actual.flatten(), prediction)
print(f'CNN-LSTM runtime: {round(time_len/60,2)} mins')
print(f"CNN-LSTM MSE: {round(mse,2)}")图18显示了CNN-LSTM模型的预测值与SP2 2天内记录的直流功率的对比。

由于CNN-LSTM的随机性,该模型运行10次,并记录一个平均MSE值作为最终值,以判断模型的性能。图19显示了为所有模型运行记录的mse的范围。

结果对比
下表显示了每个模型的MSE (CNN-LSTM的平均MSE)和每个模型的运行时间(以分钟为单位)。

从表中可以看出,XGBoost的MSE最低、运行时第二快,并且与所有其他模型相比具有最佳性能。由于该模型显示了一个可以接受的每小时预测的运行时,它可以成为帮助运营经理决策过程的强大工具。
总结
在本文中我们分析了SP1和SP2,确定SP1性能较低。所以对SP2的进一步调查显示,并且查看了SP2中那些模块性能可能有问题,并使用假设检验来计算每个模块在统计上明显表现不佳的次数,' Quc1TzYxW2pYoWX '模块显示了约850次低性能计数。
我们使用数据训练三个模型:SARIMA、XGBoost和CNN-LSTM。SARIMA表现最差,XGBOOST表现最好,MSE为16.9,运行时间为1.43 min。所以可以说XGBoost在表格数据中还是最优先得选择。
The above is the detailed content of Compare time series forecasting methods based on SARIMA, XGBoost and CNN-LSTM.. For more information, please follow other related articles on the PHP Chinese website!
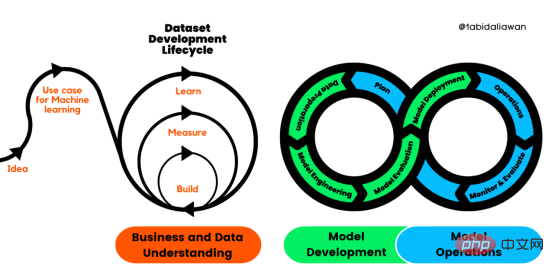 解读CRISP-ML(Q):机器学习生命周期流程Apr 08, 2023 pm 01:21 PM
解读CRISP-ML(Q):机器学习生命周期流程Apr 08, 2023 pm 01:21 PM译者 | 布加迪审校 | 孙淑娟目前,没有用于构建和管理机器学习(ML)应用程序的标准实践。机器学习项目组织得不好,缺乏可重复性,而且从长远来看容易彻底失败。因此,我们需要一套流程来帮助自己在整个机器学习生命周期中保持质量、可持续性、稳健性和成本管理。图1. 机器学习开发生命周期流程使用质量保证方法开发机器学习应用程序的跨行业标准流程(CRISP-ML(Q))是CRISP-DM的升级版,以确保机器学习产品的质量。CRISP-ML(Q)有六个单独的阶段:1. 业务和数据理解2. 数据准备3. 模型
 2023年机器学习的十大概念和技术Apr 04, 2023 pm 12:30 PM
2023年机器学习的十大概念和技术Apr 04, 2023 pm 12:30 PM机器学习是一个不断发展的学科,一直在创造新的想法和技术。本文罗列了2023年机器学习的十大概念和技术。 本文罗列了2023年机器学习的十大概念和技术。2023年机器学习的十大概念和技术是一个教计算机从数据中学习的过程,无需明确的编程。机器学习是一个不断发展的学科,一直在创造新的想法和技术。为了保持领先,数据科学家应该关注其中一些网站,以跟上最新的发展。这将有助于了解机器学习中的技术如何在实践中使用,并为自己的业务或工作领域中的可能应用提供想法。2023年机器学习的十大概念和技术:1. 深度神经网
 基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM
基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM译者 | 朱先忠审校 | 孙淑娟在我之前的博客中,我们已经了解了如何使用因果树来评估政策的异质处理效应。如果你还没有阅读过,我建议你在阅读本文前先读一遍,因为我们在本文中认为你已经了解了此文中的部分与本文相关的内容。为什么是异质处理效应(HTE:heterogenous treatment effects)呢?首先,对异质处理效应的估计允许我们根据它们的预期结果(疾病、公司收入、客户满意度等)选择提供处理(药物、广告、产品等)的用户(患者、用户、客户等)。换句话说,估计HTE有助于我
 使用PyTorch进行小样本学习的图像分类Apr 09, 2023 am 10:51 AM
使用PyTorch进行小样本学习的图像分类Apr 09, 2023 am 10:51 AM近年来,基于深度学习的模型在目标检测和图像识别等任务中表现出色。像ImageNet这样具有挑战性的图像分类数据集,包含1000种不同的对象分类,现在一些模型已经超过了人类水平上。但是这些模型依赖于监督训练流程,标记训练数据的可用性对它们有重大影响,并且模型能够检测到的类别也仅限于它们接受训练的类。由于在训练过程中没有足够的标记图像用于所有类,这些模型在现实环境中可能不太有用。并且我们希望的模型能够识别它在训练期间没有见到过的类,因为几乎不可能在所有潜在对象的图像上进行训练。我们将从几个样本中学习
 LazyPredict:为你选择最佳ML模型!Apr 06, 2023 pm 08:45 PM
LazyPredict:为你选择最佳ML模型!Apr 06, 2023 pm 08:45 PM本文讨论使用LazyPredict来创建简单的ML模型。LazyPredict创建机器学习模型的特点是不需要大量的代码,同时在不修改参数的情况下进行多模型拟合,从而在众多模型中选出性能最佳的一个。 摘要本文讨论使用LazyPredict来创建简单的ML模型。LazyPredict创建机器学习模型的特点是不需要大量的代码,同时在不修改参数的情况下进行多模型拟合,从而在众多模型中选出性能最佳的一个。本文包括的内容如下:简介LazyPredict模块的安装在分类模型中实施LazyPredict
 Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM
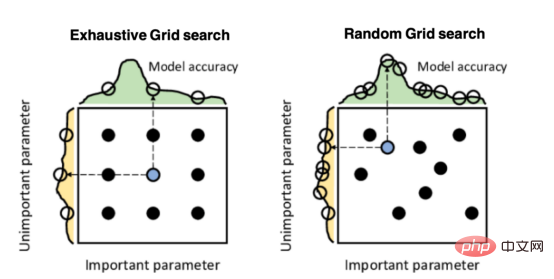
Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM译者 | 朱先忠审校 | 孙淑娟引言模型超参数(或模型设置)的优化可能是训练机器学习算法中最重要的一步,因为它可以找到最小化模型损失函数的最佳参数。这一步对于构建不易过拟合的泛化模型也是必不可少的。优化模型超参数的最著名技术是穷举网格搜索和随机网格搜索。在第一种方法中,搜索空间被定义为跨越每个模型超参数的域的网格。通过在网格的每个点上训练模型来获得最优超参数。尽管网格搜索非常容易实现,但它在计算上变得昂贵,尤其是当要优化的变量数量很大时。另一方面,随机网格搜索是一种更快的优化方法,可以提供更好的
 超参数优化比较之网格搜索、随机搜索和贝叶斯优化Apr 04, 2023 pm 12:05 PM
超参数优化比较之网格搜索、随机搜索和贝叶斯优化Apr 04, 2023 pm 12:05 PM本文将详细介绍用来提高机器学习效果的最常见的超参数优化方法。 译者 | 朱先忠审校 | 孙淑娟简介通常,在尝试改进机器学习模型时,人们首先想到的解决方案是添加更多的训练数据。额外的数据通常是有帮助(在某些情况下除外)的,但生成高质量的数据可能非常昂贵。通过使用现有数据获得最佳模型性能,超参数优化可以节省我们的时间和资源。顾名思义,超参数优化是为机器学习模型确定最佳超参数组合以满足优化函数(即,给定研究中的数据集,最大化模型的性能)的过程。换句话说,每个模型都会提供多个有关选项的调整“按钮
 人工智能自动获取知识和技能,实现自我完善的过程是什么Aug 24, 2022 am 11:57 AM
人工智能自动获取知识和技能,实现自我完善的过程是什么Aug 24, 2022 am 11:57 AM实现自我完善的过程是“机器学习”。机器学习是人工智能核心,是使计算机具有智能的根本途径;它使计算机能模拟人的学习行为,自动地通过学习来获取知识和技能,不断改善性能,实现自我完善。机器学习主要研究三方面问题:1、学习机理,人类获取知识、技能和抽象概念的天赋能力;2、学习方法,对生物学习机理进行简化的基础上,用计算的方法进行再现;3、学习系统,能够在一定程度上实现机器学习的系统。


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

WebStorm Mac version
Useful JavaScript development tools

Atom editor mac version download
The most popular open source editor

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment






