Introduction to application scenarios and implementation methods of Java heap

1. Creation of a heap

1. Adjust downward (take a small heap as an example)

Let parent mark the node that needs to be adjusted, and child mark the left child of parent (note: parent If there is a child, there must be a left child first)

If the parent's left child exists, that is: child

• Whether the right child of parent exists, find the smallest child among the left and right children, and let the child mark it

• Compare parent with the smaller child child, if:

The parent is smaller than the smaller child, and the adjustment is completed. Otherwise: exchange the parent and the smaller child. After the exchange is completed, the larger element in the parent moves downward, which may cause the subtree to not satisfy the heap. nature, so you need to continue adjusting downward, that is, parent = child; child = parent*2 1; and then continue with 2.

public void shiftDown(int[] elem,int parent,int len){
        int cur=parent*2+1;
        while(cur<len){
           if(cur+1<len){
               if(elem[cur+1]<elem[cur]){
                   cur++;
               }
           }
            if(this.elem[cur]<this.elem[parent]) {
                swap(cur, parent);
            }
            parent=cur;
            cur=parent*2+1;
        }
    }

2. Create a heap

For a normal sequence, we need to start adjusting from its first parent node with a left node until the entire tree satisfies the properties of a heap.

3. Time complexity of creating a heap

The heap must be a complete binary tree, and a full binary tree is also a complete binary tree. From the following calculation, the time complexity of creating a heap is O(n).

2. Heap insertion and deletion

1. Heap insertion

• Put the element to be inserted at the end of the heap. If it cannot be placed, expand the capacity.

• Adjust the newly inserted node upward until it is satisfied. The nature of the heap

[Upward adjustment]

public void shiftUp(int elem[],int child){
        int parent=(child-1)/2;
        while(parent>=0){
            if(elem[child]>elem[parent]){
                swap(child,parent);
                child=parent;
                parent=(child-1)/2;
            }else{
                break;
            }
        }
    }

2. Deletion of the heap

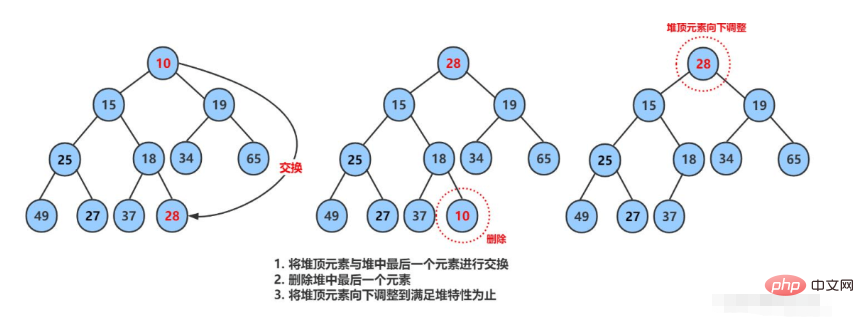
According to the nature of the heap , the deleted element must be the top element of the heap. The steps are as follows:

• Exchange the top element of the heap with the last element

• The number of elements in the heap is reduced by one

• Adjust downwards the top element of the heap

## 3. Application of heap

1. Heap sort

Ascending order: Create a large root heap

Descending order: Create a small root heap

Exchange the top element of the heap and the last element of the heap, and adjust downward until the heap is in order.

2. Top-k problem [Find the smallest K number]

top-k problem: Find the top k big or small numbers in the data set The elements generally have a relatively large amount of data.

class Solution {
    public int[] smallestK(int[] arr, int k) {
        int[] array=new int[k];
        if(arr==null||arr.length<=k||k==0){
            return array;
        }
        PriorityQueue<Integer> queue=new PriorityQueue<>((a,b)->b-a);
        int i=0;
        for(;i<k;++i){
            queue.offer(arr[i]);
        }
        while(i<arr.length){
            if(arr[i]<queue.peek()){
                queue.poll();
                queue.offer(arr[i]);
            }
            i++;
        }
        int size=queue.size();
        for(int j=0;j<size;++j){
            array[j]=queue.poll();
        }
        return array;
    }
}

IV. Introduction to common interfaces

1. Characteristics of PriorityQueue

The Java collection framework provides two types, PriorityQueue and PriorityBlockingQueue. Type of priority queue. PriorityQueue is thread-unsafe, and PriorityBlockingQueue is thread-safe. This article mainly introduces PriorityQueue.

Notes on using [PriorityQueue]:

• must import the package of PeioriryQueue;

• The placed elements must be capable Compare the size, otherwise ClassCastException will be thrown;

• Cannot place null elements, otherwise NullPointerException will be thrown;

• You can insert as many as you want The elements will be automatically expanded internally;

• The bottom layer uses a heap data structure, and the default is a small heap. If you want to build a large heap, you need to provide a comparator.

PriorityQueue expansion method:

• If the capacity is less than 64, it will be expanded by 2 times the oldCapacity

• If the capacity is greater than or equal to 64, it is expanded according to 1.5 times of oldCapacity

• If the capacity exceeds MAX_ARRAY_SIZE, it is expanded according to MAX_ARRAY_SIZE

int newCapacity = oldCapacity ((oldCapacity                               (oldCapacity 2) :

                                                                                                                        (oldCapacity             );

PriorityQueue uses two methods: Comparble and Comparator.

1. Comparble is the default internal comparison method. If the user inserts a custom type object, the object must implement the Comparble interface and override the compareTo method

2. Users can also If you choose to use a comparator object, if the user inserts a custom type object, you must provide a comparator class that implements the Comparator interface and overrides the compare method

// 用户自己定义的比较器：直接实现Comparator接口，然后重写该接口中的compare方法即可
class IntCmp implements Comparator<Integer>{
   @Override
   public int compare(Integer o1, Integer o2) {
      return o2-o1;
   }
}
PriorityQueue<Integer> p = new PriorityQueue<>(new IntCmp());

2、优先级队列的构造

构造器	功能介绍
PriorityQueue()	创建一个空的优先级队列，默认容量是11
PriorityQueue(int initialCapacity)	创建一个初始容量为initialCapacity的优先级队列，注意： initialCapacity不能小于1，否则会抛IllegalArgumentException异 常
PriorityQueue(Collection extends E> c)	用一个集合来创建优先级队列

The above is the detailed content of Introduction to application scenarios and implementation methods of Java heap. For more information, please follow other related articles on the PHP Chinese website!