Java algorithm design and analysis: detailed explanation of divide-and-conquer algorithm examples

##1. Preface

Before learning the divide-and-conquer algorithm, let me ask you a question. I believe everyone has the experience of piggy banks when they were young. If your parents and relatives If you give money, you will put it into your own treasure. We will count the money every once in a while. But you may find it complicated to handle a pile of money, because the data is a bit huge compared to your brain, and it is easy to make mistakes. You may divide it into several small parts and then add them up to calculate the total. The total amount of this pile of money

Of course, if you feel that the amount of each part of the money is still too large, you can still divide and merge it. The reason why we have so many is:

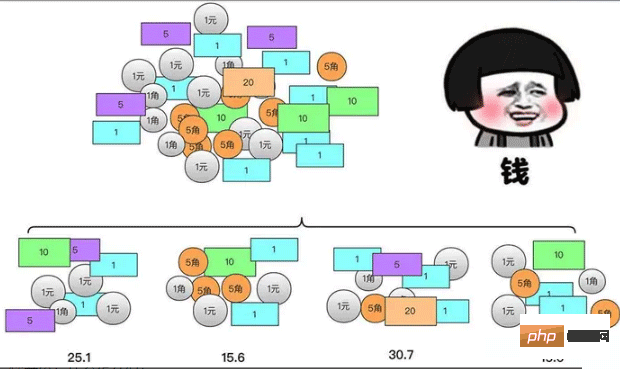
• The way to calculate each small pile of money is the same as the way to calculate the largest pile of money (the difference lies in the size)

• Then the big The sum of the piles of money is actually the sum of the results of the small piles of money. In this way, there is actually a divide and conquer mentality.

2. Introduction to the divide-and-conquer algorithm

The divide-and-conquer algorithm is an algorithm that uses the divide-and-conquer idea. What is divide-and-conquer?

Divide and conquer, the literal explanation is "divide and conquer", which is to divide a complex problem into two or more identical or similar sub-problems, and then divide the sub-problems into smaller sub-problems... …Until the end, the sub-problem can be solved simply and directly, and the solution to the original problem is the combination of the solutions to the sub-problem. In computer science, the divide-and-conquer method is a very important algorithm that uses the divide-and-conquer idea. The divide-and-conquer method is the basis of many efficient algorithms, such as sorting algorithms (quick sort, merge sort), Fourier transform (fast Fourier transform), etc.

Decompose the parent problem into sub-problems and solve them in the same way. This is consistent with the concept of recursion, so the divide-and-conquer algorithm is usually implemented in a recursive way (of course there are also non-recursive implementations).

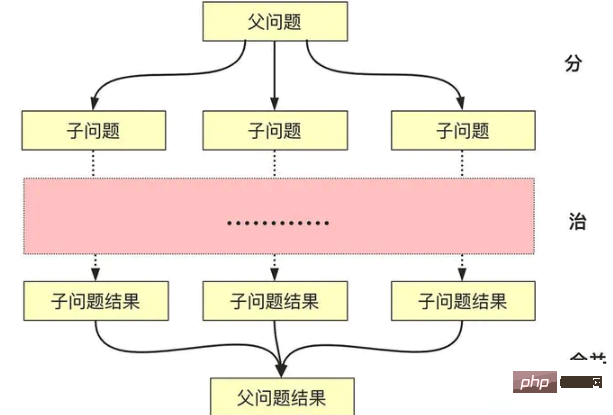
The description of the divide-and-conquer algorithm is easy to understand literally. Divide and conquer actually involve a merging process:

• Divide: Recursively solve smaller problems (stop when reaching the termination layer or when it can be solved)

• Conquer: Solve recursively, or solve directly if the problem is small enough.

• Combine: Construct the solution of the sub-problem into the parent class problem

The general divide-and-conquer algorithm is in the text It is decomposed into two or more recursive calls, and subclass issues generally do not want to be crossed (do not affect each other). When solving a problem that is very large and difficult to solve directly, but is easy to solve when it is small and the problem meets the applicable conditions of the divide-and-conquer algorithm, then the divide-and-conquer algorithm can be used.

So what conditions (characteristics) need to be met for problems solved by the divide-and-conquer algorithm?

## 1. The scale of the original problem is usually relatively large and difficult to solve directly, but it can be solved more easily when the problem is reduced to a certain extent.
2. The problem can be decomposed into a number of smaller sub-problems with the same (similar) solution method. And the solutions to the sub-problems are independent and do not affect each other.
3. The solution to the problem can be obtained by merging the sub-problems decomposed into the problem.
You may be wondering what the relationship between the divide-and-conquer algorithm and recursion is? In fact, divide and conquer is an important thought, focusing on the process of dividing, conquering and merging problems. Recursion is a method (tool) that uses methods to call themselves to form a back-and-forth process, and divide and conquer may take advantage of multiple such back-and-forth processes.

3. Classic Problems of the Divide and Conquer Algorithm

For the classic problems of the divide and conquer algorithm, what is important is its idea. Because we mostly use recursion to implement it, most of the code implementation is It is very simple, and this article also focuses on the thoughts.

The classic problem of the divide-and-conquer algorithm is divided into two categories: sub-problems are completely independent and sub-problems are not completely independent.

1. The sub-problems are completely independent, which means that the answer to the original question can be completely derived from the results of the sub-problems.
2. The sub-problems are not completely independent. For some interval problems or cross-interval problems, the results of divide and conquer may span across intervals. You need to learn from it carefully when considering the problem.
3.1. Binary search

Binary search is an example of divide and conquer, but binary search has its own particularity

Sequence order
The result is a value
Normal bisection divides a complete interval into two intervals, and the two intervals should be Find the value separately and then confirm the result, but you can directly determine which interval the result is in through the ordered interval, so you only need to calculate one of the two intervals, and then continue until the end. There are recursive and non-recursive implementation methods, but non-recursive is more commonly used:

public int searchInsert(int[] nums, int target) {
  if(nums[0]>=target)return 0;//剪枝
  if(nums[nums.length-1]==target)return nums.length-1;//剪枝
  if(nums[nums.length-1]<target)return nums.length;
  int left=0,right=nums.length-1;
  while (left<right) {
    int mid=(left+right)/2;
    if(nums[mid]==target)
      return mid;
    else if (nums[mid]>target) {
      right=mid;
    }
    else {
      left=mid+1;
    }
  }
  return left;
}

3.2. Quick sort

Quick sort is also an example of divide and conquer. Each pass of quick sort will select a number, and put the number smaller than this number on the left, and the number larger than this number on the right. , and then recursively divide and conquer to solve the two sub-intervals. Of course, quick sort does a lot of work when dividing. When all the parts are at the bottom, the value of this sequence is the sorted value. This is a manifestation of divide and conquer.

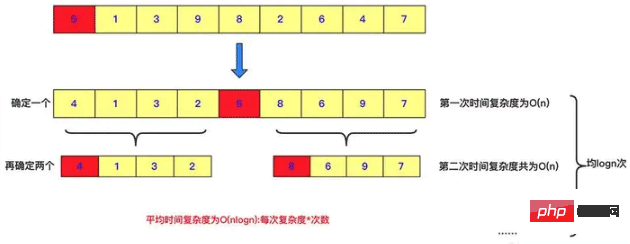
public void quicksort(int [] a,int left,int right)
{
  int low=left;
  int high=right;
  //下面两句的顺序一定不能混，否则会产生数组越界！！！very important！！！
  if(low>high)//作为判断是否截止条件
    return;
  int k=a[low];//额外空间k，取最左侧的一个作为衡量，最后要求左侧都比它小，右侧都比它大。
  while(low<high)//这一轮要求把左侧小于a[low],右侧大于a[low]。
  {
    while(low<high&&a[high]>=k)//右侧找到第一个小于k的停止
    {
      high--;
    }
    //这样就找到第一个比它小的了
    a[low]=a[high];//放到low位置
    while(low<high&&a[low]<=k)//在low往右找到第一个大于k的，放到右侧a[high]位置
    {
      low++;
    }
    a[high]=a[low];
  }
  a[low]=k;//赋值然后左右递归分治求之
  quicksort(a, left, low-1);
  quicksort(a, low+1, right);
}

3.3. Merge sort (reverse order)

Quick sort does a lot of work when dividing, and merging is the opposite. When merging, they are evenly divided according to the number, and when merging, they are already merged in an orderly manner, because the required results can be obtained with the O(n) level complexity of two ordered sequences. The deformation of reverse ordinal numbers based on merge sorting is also solved by the divide and conquer idea.

private static void mergesort(int[] array, int left, int right) {
  int mid=(left+right)/2;
  if(left<right)
  {
    mergesort(array, left, mid);
    mergesort(array, mid+1, right);
    merge(array, left,mid, right);
  }
}
private static void merge(int[] array, int l, int mid, int r) {
  int lindex=l;int rindex=mid+1;
  int team[]=new int[r-l+1];
  int teamindex=0;
  while (lindex<=mid&&rindex<=r) {//先左右比较合并
    if(array[lindex]<=array[rindex])
    {
      team[teamindex++]=array[lindex++];
    }
    else {
      team[teamindex++]=array[rindex++];
    }
  }
  while(lindex<=mid)//当一个越界后剩余按序列添加即可
  {
    team[teamindex++]=array[lindex++];

  }
  while(rindex<=r)
  {
    team[teamindex++]=array[rindex++];
  }	
  for(int i=0;i<teamindex;i++)
  {
    array[l+i]=team[i];
  }
}

3.4. We can use dynamic programming to solve the problem of maximum subsequence and

maximum sum of subsequences, but we can also use the divide-and-conquer algorithm. Solve the problem, but the maximum subsequence sum is not a simple merge when merging, because the subsequence sum involves a length problem, so the correct results are not necessarily all on the leftmost or rightmost, but the area where the result may appear For:

• completely to the left of the center

• completely to the right of the center

• A sequence containing the left and right nodes in the middle

can be represented by a graph as:

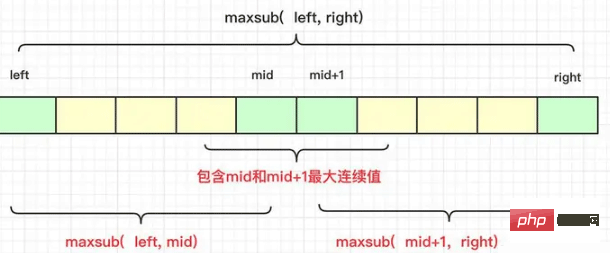
Therefore, when considering it specifically, it is necessary to calculate the result of the maximum value string in the middle that cannot be obtained recursively to participate in the comparison between the left and right sides.

The code for the maximum subsequence sum is:

public int maxSubArray(int[] nums) {
    int max=maxsub(nums,0,nums.length-1);
    return max;
}
int maxsub(int nums[],int left,int right)
{
    if(left==right)
        return  nums[left];
    int mid=(left+right)/2;
    int leftmax=maxsub(nums,left,mid);//左侧最大
    int rightmax=maxsub(nums,mid+1,right);//右侧最大
    int midleft=nums[mid];//中间往左
    int midright=nums[mid+1];//中间往右
    int team=0;
    for(int i=mid;i>=left;i--)
    {
        team+=nums[i];
        if(team>midleft)
            midleft=team;
    }
    team=0;
    for(int i=mid+1;i<=right;i++)
    {
        team+=nums[i];
        if(team>midright)
            midright=team;
    }
    int max=midleft+midright;//中间的最大值
    if(max<leftmax)
        max=leftmax;
    if(max<rightmax)
        max=rightmax;
    return  max;
}

3.5. Nearest point pair

The nearest point pair is a very successful divide and conquer method One of the applications. There are several point coordinates on the two-dimensional coordinate axis, allowing you to find the distance between the two nearest points. If you are asked to find it directly, enumeration violence is a very, very large amount of calculation. We usually use the divide and conquer method to optimize This kind of problem.

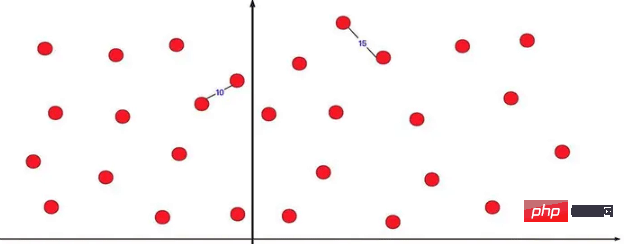
If you directly divide it into two parts and calculate the divide and conquer, you will definitely find that if the shortest one is on the left and the other on the right, there will be a problem. We can optimize it.

In terms of the specific optimization plan, consider the x or y dimension, divide the data into two areas, and first calculate (according to the same method) the shortest point pairs in the left and right areas respectively. Then cover it to the left and right according to the shorter distance between the two, calculate the distance between the covered left and right points, find the smallest distance and compare it with the current shortest distance.

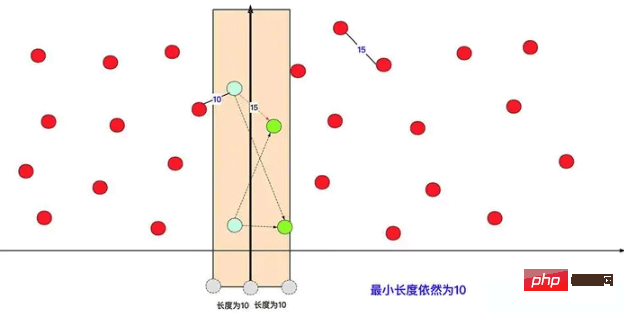
In this way, you can find that in this one-time operation (regardless of sub-cases), the red point on the left avoids distance calculation with most of the red points on the right (O (time complexity of n2)). In fact, when performing internal calculations in the left and right intervals, it actually performs many divide-and-conquer calculations recursively. As shown in the figure:

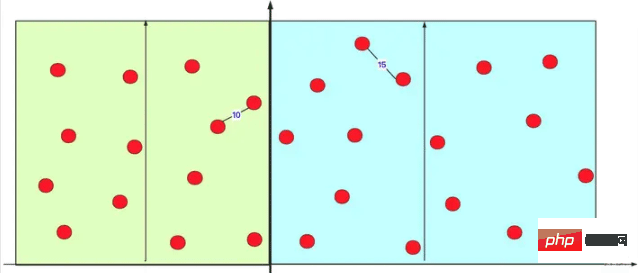
# This can save many calculations.

However, there is a problem with this kind of divide and conquer. The two-dimensional coordinates may have points clustered on a certain method and a certain axis, so the effect may not be obvious (the points are all near x=2 and have no effect on x division). Large), you need to pay attention to it. The code for

ac is:

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.List;
public class Main {
    static int n;
    public static void main(String[] args) throws IOException {
        StreamTokenizer in=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        //List<node>list=new ArrayList();
         while(in.nextToken()!=StreamTokenizer.TT_EOF)
         {
             n=(int)in.nval;if(n==0) {break;}
            node no[]=new node[n];

             for(int i=0;i<n;i++)
             {
                 in.nextToken();double x=in.nval;
                 in.nextToken();double y=in.nval;
                // list.add(new node(x,y));
                 no[i]=new node(x,y);
             }
             Arrays.sort(no, com);
            double min= search(no,0,n-1);
            out.println(String.format("%.2f", Math.sqrt(min)/2));out.flush();
         }
    }
    private static double search(node[] no, int left,int right) {
        int mid=(right+left)/2;
        double minleng=0;
        if(left==right) {return Double.MAX_VALUE;}
        else if(left+1==right) {minleng= (no[left].x-no[right].x)*(no[left].x-no[right].x)+(no[left].y-no[right].y)*(no[left].y-no[right].y);}
        else minleng= min(search(no,left,mid),search(no,mid,right));
        int ll=mid;int rr=mid+1;
        while(no[mid].y-no[ll].y<=Math.sqrt(minleng)/2&&ll-1>=left) {ll--;}
        while(no[rr].y-no[mid].y<=Math.sqrt(minleng)/2&&rr+1<=right) {rr++;}
        for(int i=ll;i<rr;i++)
        {
            for(int j=i+1;j<rr+1;j++)
            {
                double team=0;
                if(Math.abs((no[i].x-no[j].x)*(no[i].x-no[j].x))>minleng) {continue;}
                else
                {
                    team=(no[i].x-no[j].x)*(no[i].x-no[j].x)+(no[i].y-no[j].y)*(no[i].y-no[j].y);
                    if(team<minleng)minleng=team;
                }
            }
        }
        return minleng;

    }
    private static double min(double a, double b) {
        // TODO 自动生成的方法存根
        return a<b?a:b;
    }
    static Comparator<node>com=new Comparator<node>() {

        @Override
        public int compare(node a1, node a2) {
            // TODO 自动生成的方法存根
            return a1.y-a2.y>0?1:-1;
        }};
    static class node
    {
        double x;
        double y;
        public node(double x,double y)
        {
            this.x=x;
            this.y=y;
        }
    }
}

The above is the detailed content of Java algorithm design and analysis: detailed explanation of divide-and-conquer algorithm examples. For more information, please follow other related articles on the PHP Chinese website!