How to implement a genetic algorithm using Python

Genetic algorithm is a stochastic global search and optimization method developed to imitate the biological evolution mechanism in nature. It draws on Darwin's theory of evolution and Mendel's theory of genetics. Its essence is an efficient, parallel, global search method that can automatically acquire and accumulate knowledge about the search space during the search process, and adaptively control the search process to obtain the optimal solution. Genetic algorithm operations use the principle of survival of the fittest to successively generate a near-optimal solution in the potential solution population. In each generation of the genetic algorithm, according to the fitness value of the individual in the problem domain and from natural genetics The reconstruction method borrowed from Chinese literature is used for individual selection to generate a new approximate solution. This process leads to the evolution of individuals in the population, and the resulting new individuals are better adapted to the environment than the original individuals, just like transformation in nature.

Specific steps of the genetic algorithm:

(1) Initialization: Set the evolutionary generation counter t=0, set the maximum evolutionary generation T, crossover probability, mutation probability, and randomly generate M individuals as the initial population. P

(2) Individual evaluation: Calculate the fitness of each individual in the population P

(3) Selection operation: Apply the selection operator to the population. Based on individual fitness, select the optimal individual to directly inherit it to the next generation or generate new individuals through paired crossover and then inherit it to the next generation

(4) Crossover operation: Under the control of crossover probability, the population Individuals in the population are crossed in pairs

(5) Mutation operation: Under the control of mutation probability, individuals in the population are mutated, that is, the genes of a certain individual are randomly adjusted

(6) After selection, crossover, and mutation operations, the next generation population P1 is obtained.

Repeat the above (1)-(6) until the genetic generation is T, use the individual with the optimal fitness obtained during the evolution process as the optimal solution output, and terminate the calculation.

Traveling Salesman Problem (TSP): There are n cities. A salesman must start from one of the cities, visit all the cities, and then return to the city where he started. Find The shortest route.

Some conventions need to be made when applying genetic algorithms to solve TSP problems. A gene is a set of city sequences, and the fitness is one-third of the distance and the sequence of cities according to this gene.

1.2 Experimental code

import random
import math
import matplotlib.pyplot as plt
# 读取数据
f=open("test.txt")
data=f.readlines()
# 将cities初始化为字典，防止下面被当成列表
cities={}
for line in data:
    #原始数据以\n换行，将其替换掉
    line=line.replace("\n","")
    #最后一行以EOF为标志，如果读到就证明读完了，退出循环
    if(line=="EOF"):
        break
    #空格分割城市编号和城市的坐标
    city=line.split(" ")
    map(int,city)
    #将城市数据添加到cities中
    cities[eval(city[0])]=[eval(city[1]),eval(city[2])]
 
# 计算适应度，也就是距离分之一，这里用伪欧氏距离
def calcfit(gene):
    sum=0
    #最后要回到初始城市所以从-1，也就是最后一个城市绕一圈到最后一个城市
    for i in range(-1,len(gene)-1):
        nowcity=gene[i]
        nextcity=gene[i+1]
        nowloc=cities[nowcity]
        nextloc=cities[nextcity]
        sum+=math.sqrt(((nowloc[0]-nextloc[0])**2+(nowloc[1]-nextloc[1])**2)/10)
 
    return 1/sum
 
# 每个个体的类，方便根据基因计算适应度
class Person:
    def __init__(self,gene):
        self.gene=gene
        self.fit=calcfit(gene)
class Group:
    def __init__(self):
        self.GroupSize=100  #种群规模
        self.GeneSize=48    #基因数量，也就是城市数量
        self.initGroup()
        self.upDate()
    #初始化种群，随机生成若干个体
    def initGroup(self):
        self.group=[]
        i=0
        while(i<self.GroupSize):
            i+=1
            #gene如果在for以外生成只会shuffle一次
            gene=[i+1 for i in range(self.GeneSize)]
            random.shuffle(gene)
            tmpPerson=Person(gene)
            self.group.append(tmpPerson)
 
    #获取种群中适应度最高的个体
    def getBest(self):
        bestFit=self.group[0].fit
        best=self.group[0]
        for person in self.group:
            if(person.fit>bestFit):
                bestFit=person.fit
                best=person
        return best
    #计算种群中所有个体的平均距离
    def getAvg(self):
        sum=0
        for p in self.group:
            sum+=1/p.fit
        return sum/len(self.group)
    #根据适应度，使用轮盘赌返回一个个体，用于遗传交叉
    def getOne(self):
        #section的简称，区间
        sec=[0]
        sumsec=0
        for person in self.group:
            sumsec+=person.fit
            sec.append(sumsec)
        p=random.random()*sumsec
        for i in range(len(sec)):
            if(p>sec[i] and p<sec[i+1]):
                #这里注意区间是比个体多一个0的
                return self.group[i]
    #更新种群相关信息
    def upDate(self):
        self.best=self.getBest()
# 遗传算法的类，定义了遗传、交叉、变异等操作
class GA:
    def __init__(self):
        self.group=Group()
        self.pCross=0.35    #交叉率
        self.pChange=0.1    #变异率
        self.Gen=1  #代数
 
    #变异操作
    def change(self,gene):
        #把列表随机的一段取出然后再随机插入某个位置
        #length是取出基因的长度，postake是取出的位置，posins是插入的位置
        geneLenght=len(gene)
        index1 = random.randint(0, geneLenght - 1)
        index2 = random.randint(0, geneLenght - 1)
        newGene = gene[:]       # 产生一个新的基因序列，以免变异的时候影响父种群
        newGene[index1], newGene[index2] = newGene[index2], newGene[index1]
        return newGene
 
    #交叉操作
    def cross(self,p1,p2):
        geneLenght=len(p1.gene)
        index1 = random.randint(0, geneLenght - 1)
        index2 = random.randint(index1, geneLenght - 1)
        tempGene = p2.gene[index1:index2]   # 交叉的基因片段
        newGene = []
        p1len = 0
        for g in p1.gene:
              if p1len == index1:
                    newGene.extend(tempGene)     # 插入基因片段
                    p1len += 1
              if g not in tempGene:
                    newGene.append(g)
                    p1len += 1
        return newGene
 
    #获取下一代
    def nextGen(self):
        self.Gen+=1
        #nextGen代表下一代的所有基因
        nextGen=[]
        #将最优秀的基因直接传递给下一代
        nextGen.append(self.group.getBest().gene[:])
        while(len(nextGen)<self.group.GroupSize):
            pChange=random.random()
            pCross=random.random()
            p1=self.group.getOne()
            if(pCross<self.pCross):
                p2=self.group.getOne()
                newGene=self.cross(p1,p2)
            else:
                newGene=p1.gene[:]
            if(pChange<self.pChange):
                newGene=self.change(newGene)
            nextGen.append(newGene)
        self.group.group=[]
        for gene in nextGen:
            self.group.group.append(Person(gene))
            self.group.upDate()
 
    #打印当前种群的最优个体信息
    def showBest(self):
        print("第{}代\t当前最优{}\t当前平均{}\t".format(self.Gen,1/self.group.getBest().fit,self.group.getAvg()))
 
    #n代表代数，遗传算法的入口
    def run(self,n):
        Gen=[]  #代数
        dist=[] #每一代的最优距离
        avgDist=[]  #每一代的平均距离
        #上面三个列表是为了画图
        i=1
        while(i<n):
            self.nextGen()
            self.showBest()
            i+=1
            Gen.append(i)
            dist.append(1/self.group.getBest().fit)
            avgDist.append(self.group.getAvg())
        #绘制进化曲线
        plt.plot(Gen,dist,&#39;-r&#39;)
        plt.plot(Gen,avgDist,&#39;-b&#39;)
        plt.show()
 
ga=GA()
ga.run(3000)
print("进行3000代后最优解：",1/ga.group.getBest().fit)

1.3 Experimental results

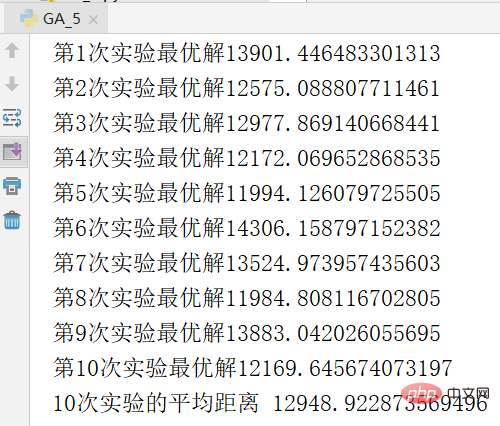
The picture below is a screenshot of the results of an experiment. The optimal solution is 11271

In order to avoid the contingency of the experiment, the experiment was repeated 10 times and the average value was calculated. The results are as follows.

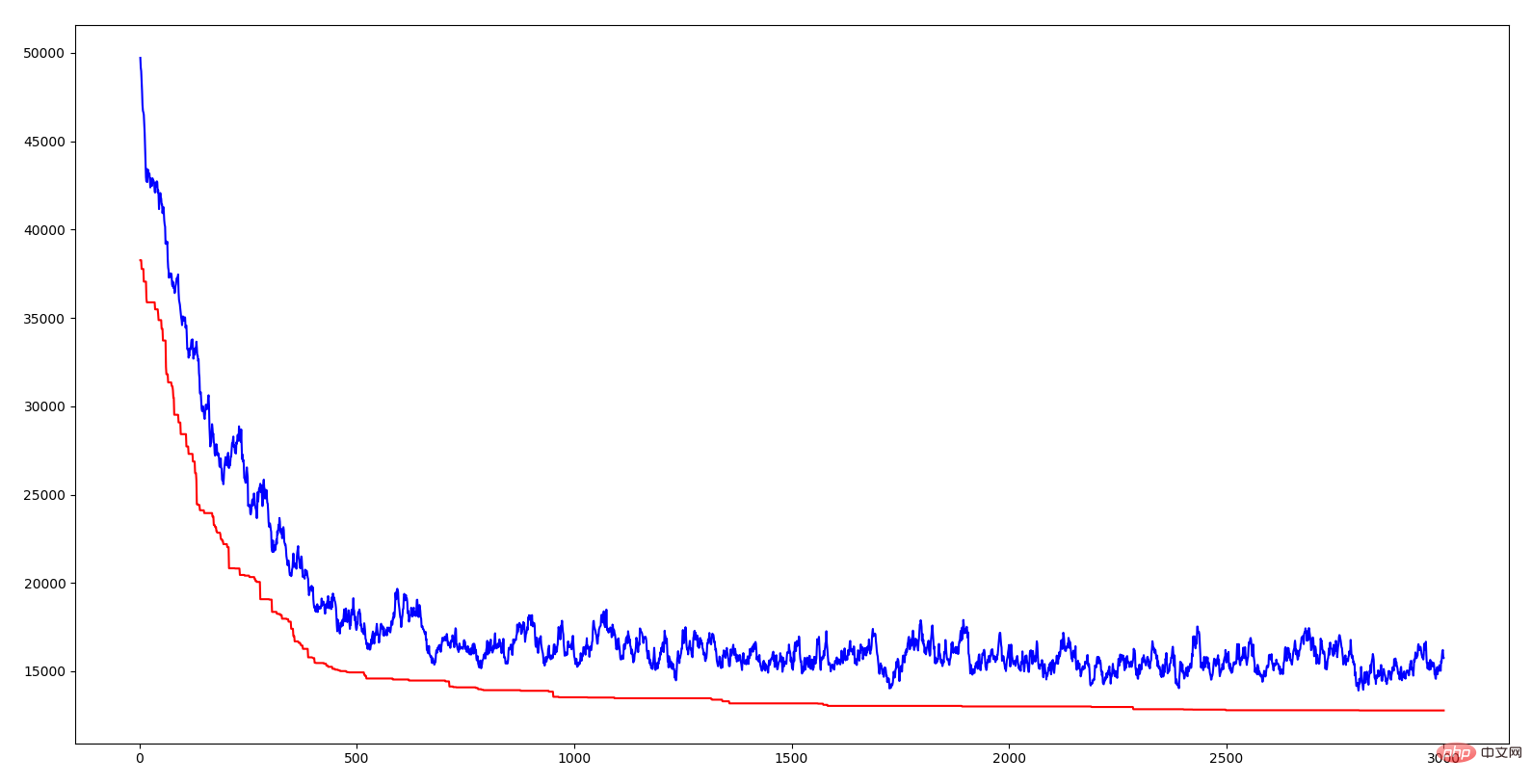
The abscissa of the above figure is the algebra, the ordinate is the distance, the red curve is the distance of the optimal individual of each generation, and the blue The curve is the average distance for each generation. It can be seen that both lines are trending downward, which means they are evolving. The decrease in average distance indicates that due to the emergence of excellent genes (that is, a certain urban sequence), this excellent trait quickly spreads to the entire population. Just like the survival of the fittest in nature, only those with genes that adapt to the environment can survive. Correspondingly, those who survive are those with excellent genes. The significance of introducing crossover rate and mutation rate in the algorithm is to ensure the current excellent genes and try to generate better genes. If all individuals cross over, some excellent gene segments may be lost; if none cross over, then two excellent gene segments cannot be combined into better genes; if there is no variation, individuals more adapted to the environment cannot be produced. I have to sigh that the wisdom of nature is so powerful.

The gene fragment mentioned above is a short city sequence in TSP. When the distance sum of a certain sequence is relatively small, it means that this sequence is a relatively good traversal order for these cities. The genetic algorithm achieves continuous optimization of the TSP solution by combining these excellent fragments. The combination method draws on the wisdom of nature, inheritance, mutation, and survival of the fittest.

1.4 Experiment Summary

1. How to achieve "survival of the fittest" in the algorithm?

The so-called survival of the fittest means the retention of excellent genes and the elimination of genes that are not suitable for the environment. In the above GA algorithm, I use roulette, that is, in the genetic step (whether crossover or not), each individual is selected based on its fitness. In this way, individuals with high fitness can have more offspring, thus achieving the purpose of survival of the fittest.

During the specific implementation process, I made a mistake. At first, when screening individuals in the genetic step, every time I selected an individual, I deleted this individual from the group. Thinking about it now, this approach was very stupid. Although I had already implemented roulette at the time, if the individual was selected and deleted, it would cause each individual to give birth to offspring equally. The so-called roulette is just a way to Let those with high fitness be inherited first. This approach completely deviates from the original intention of "survival of the fittest". The correct approach is to select individuals for inheritance and then put them back into the population. This can ensure that individuals with high fitness will be inherited multiple times, produce more offspring, and spread excellent genes more widely. At the same time, unfit individuals will Produce few offspring or be eliminated directly.

2. How to ensure that evolution is always progressing in the positive direction?

The so-called forward progression means that the optimal individuals of the next generation must be more or equally adaptable to the environment than the previous generation. The method I adopt is that the optimal individual directly enters the next generation without participating in operations such as crossover mutation. This can prevent reverse evolution from "contaminating" the best genes currently due to these operations.

I also encountered another problem during the implementation process, whether it was caused by passing by reference or by value. A list is used for crossover and mutation of individual genes. When passing the list in Python, it is actually a reference. This will cause the individual's own genes to be changed after crossover and mutation. The result is very slow evolution, accompanied by reverse evolution.

3. How to achieve crossover?

Select the fragments of one individual and put them into another individual, and put the non-duplicated genes into other positions in sequence.

When implementing this step, I incorrectly implemented this function because of my inherent understanding of the behavior of real chromosomes when studying biology, "homologous chromosomes cross and exchange homologous segments." I only interchanged the fragments of the two individuals at the same position to complete the crossover. Obviously this approach is wrong and will lead to the duplication of cities.

4. When I first started writing this algorithm, I wrote it half OOP and half process-oriented.

During subsequent testing, I found that it was troublesome to change parameters and update individual information, so I changed everything to OOP, which was much more convenient. OOP offers great flexibility and simplicity for simulating real-world problems like this.

5. How to prevent the occurrence of local optimal solutions?

During the testing process, it was found that local optimal solutions occasionally appear, which will not continue to evolve for a long time, and the solution at this time is far away from the optimal solution. Even after subsequent adjustments, although it is close to the optimal solution, it is still a "local optimal" because it has not yet reached the optimal solution.

The algorithm will converge quickly at the beginning, but will become slower and slower as it goes on, or even not move at all. Because in the later stage, all individuals have relatively similar excellent genes, the effect of crossover on evolution at this time is very weak, and the main driving force of evolution becomes mutation, and mutation is a violent algorithm. If you're lucky, you can mutate into a better individual quickly, but if you're not lucky, you'll have to wait.

The solution to prevent local optimal solutions is to increase the size of the population, so that there will be more individual mutations, and there will be a greater possibility of producing evolved individuals. The disadvantage of increasing the population size is that the calculation time of each generation will become longer, which means that the two inhibit each other. Although a huge population size can ultimately avoid the local optimal solution, each generation takes a long time and it takes a long time to find the optimal solution; while a smaller population size, although the calculation time of each generation is fast, will not be solved after several generations. will fall into a local optimum.

I guess a possible optimization method is to use a smaller population size in the early stages of evolution to speed up evolution. When the fitness reaches a certain threshold, increase the population size and mutation rate to avoid local maxima. The emergence of superior solutions. This dynamic adjustment method is used to weigh the balance between the computing efficiency of each generation and the overall computing efficiency.

The above is the detailed content of How to implement a genetic algorithm using Python. For more information, please follow other related articles on the PHP Chinese website!