 Technology peripherals
Technology peripherals AI
AI Learning = fitting? Are deep learning and classic statistics the same thing?
Learning = fitting? Are deep learning and classic statistics the same thing?Learning = fitting? Are deep learning and classic statistics the same thing?
In this article, Boaz Barak, a theoretical computer scientist and well-known professor at Harvard University, compares the differences between deep learning and classical statistics in detail. He believes that "if you understand deep learning purely from a statistical perspective, you will ignore its successful results." The key factor".
Deep learning (or machine learning in general) is often thought of as simply statistics, that is, it is basically the same concept that statisticians study, but is described using different terminology than statistics. Rob Tibshirani once summed up this interesting “glossary” below:

Does something in this list really resonate? Virtually anyone involved in machine learning knows that many of the terms on the right side of the table posted by Tibshiriani are widely used in machine learning.
If you understand deep learning purely from a statistical perspective, you will ignore the key factors for its success. A more appropriate assessment of deep learning is that it uses statistical terms to describe completely different concepts.
The proper assessment of deep learning is not that it uses different words to describe old statistical terms, but that it uses these terms to describe completely different processes.
This article will explain why the foundation of deep learning is actually different from statistics, or even different from classic machine learning. This article first discusses the difference between the "explanation" task and the "prediction" task when fitting a model to data. Two scenarios of the learning process are then discussed: 1. Fitting statistical models using empirical risk minimization; 2. Teaching mathematical skills to students. Then, the article discusses which scenario is closer to the essence of deep learning.
Although the mathematics and code of deep learning are almost the same as fitting statistical models. But on a deeper level, deep learning is more like teaching math skills to students. And there should be very few people who dare to claim: I have mastered the complete deep learning theory! In fact, it is doubtful whether such a theory exists. Instead different aspects of deep learning are best understood from different perspectives, and statistics alone cannot provide a complete picture.
This article compares deep learning and statistics. Statistics here specifically refers to "classical statistics" because it has been studied for the longest time and has been in textbooks for a long time. Many statisticians are working on deep learning and non-classical theoretical methods, just as 20th century physicists needed to expand the framework of classical physics. In fact, blurring the lines between computer scientists and statisticians benefits both parties.
Prediction and Model Fitting
Scientists have always compared model calculation results with actual observation results to verify the accuracy of the model. The Egyptian astronomer Ptolemy proposed an ingenious model of planetary motion. Ptolemy's model followed geocentrism but had a series of epicycles (see diagram below), giving it excellent predictive accuracy. In contrast, Copernicus' original heliocentric model was simpler than the Ptolemaic model but less accurate in predicting observations. (Copernicus later added his own epicycles to be comparable to Ptolemy's model.)

Both Ptolemy's and Copernicus' models were unparalleled of. If we want to make predictions through a "black box", then Ptolemy's geocentric model is superior. But if you want a simple model that you can "look inside" (which is the starting point for theories that explain stellar motion), then Copernicus's model is the way to go. Later, Kepler improved Copernicus' model into an elliptical orbit and proposed Kepler's three laws of planetary motion, which enabled Newton to explain planetary laws with the law of gravity applicable to the earth.
It is therefore important that the heliocentric model is not just a "black box" that provides predictions, but is given by a few simple mathematical equations, but with very few "moving parts" in the equations. Astronomy has been a source of inspiration for developing statistical techniques for many years. Gauss and Legendre independently invented least squares regression around 1800 to predict the orbits of asteroids and other celestial bodies. In 1847, Cauchy invented the gradient descent method, which was also motivated by astronomical predictions.
In physics, sometimes scholars can master all the details to find the “right” theory, maximize the accuracy of predictions, and provide the best explanation of the data. These are within the scope of ideas such as Occam's razor, which can be thought of as assuming that simplicity, predictive power, and explanatory power are all in harmony with each other.
However, in many other fields, the relationship between the two goals of explanation and prediction is not so harmonious. If you just want to predict observations, going through a "black box" is probably best. On the other hand, if one wants to obtain explanatory information, such as causal models, general principles, or important features, then the simpler the model that can be understood and explained, the better.
The correct choice of model depends on its purpose. For example, consider a dataset that contains the genetic expression and phenotypes of many individuals (e.g., some disease). If the goal is to predict a person's chance of getting sick, then no matter how complex it is or how many genes it relies on, use The best predictive model adapted to the task. On the contrary, if the aim is to identify a few genes for further study, then a complex and very precise "black box" is of limited use.
Statistician Leo Breiman made this point in his famous 2001 article on the two cultures of statistical modeling. The first is a "data modeling culture" that focuses on simple generative models that can explain the data. The second is an “algorithmic modeling culture” that is agnostic about how the data was generated and focuses on finding models that can predict the data, no matter how complex.

Paper title:
Statistical Modeling: The Two Cultures
Paper link:
https://projecteuclid .org/euclid.ss/1009213726
Breiman believes that statistics is too dominated by the first culture, and this focus creates two problems:
- Leads to irrelevant Theories and dubious scientific conclusions prevent statisticians from studying exciting new problems. Breiman's paper caused some controversy when it came out. Fellow statistician Brad Efron responded that while he agreed with some of the points, he also emphasized that Breiman's argument seemed to be against frugality and scientific insight in favor of going to great lengths to create complex "black boxes." But in a recent article, Efron abandoned his previous view and admitted that Breima was more prescient because "the focus of statistics in the 21st century is on predictive algorithms, which have evolved to a large extent along the lines proposed by Breiman." .
- Classic and Modern Predictive Models
Excerpts from Duda and Hart's textbook "Pattern classification and scene analysis" and Highleyman's 1962 paper "The Design and Analysis of Pattern Recognition Experiments".
Similarly, the image below of Highleyman's handwritten character data set and the architecture used to fit it, Chow (1962) (accuracy ~58%), will resonate with many people. 
Why is deep learning different?
In 1992, Geman, Bienenstock, and Doursat wrote a pessimistic article about neural networks, arguing that "current feedforward neural networks are largely insufficient to solve difficult problems in machine perception and machine learning." . Specifically, they argue that general-purpose neural networks will not succeed at handling difficult tasks, and that the only way they can succeed is through artificially designed features. In their words: "The important properties must be built-in or "hard-wired"... rather than learned in any statistical sense." Now it seems that Geman et al. are completely wrong, but it is more interesting to understand why they wrong. 
(
is the matrix of;
is the-dimensional vector, that is, the category label. Thinking that the data comes from a model that has structure and contains noise is the model to be fitted)
2. Use the above data to fit a model , and use an optimization algorithm to minimize the empirical risk. That is to say, find such
, and use an optimization algorithm to minimize the empirical risk. That is to say, find such  through the optimization algorithm so that
through the optimization algorithm so that  is the smallest,
is the smallest,  represents the loss (indicating how close the predicted value is to the true value), and
represents the loss (indicating how close the predicted value is to the true value), and  is an optional regularization term.
is an optional regularization term.
3. The smaller the overall loss of the model, the better, that is, the value of the generalization error  is relatively minimal.
is relatively minimal.

Effron Demonstration of recovering Newton's first law from observations containing noise
This very general example actually contains many contents, such as least squares Linear regression, nearest neighbor, neural network training and more. In classic statistical scenarios, we usually encounter the following situation:
Trade-off: Assuming an optimized collection of models (if the function is non-convex or contains regularization terms, careful selection of algorithms and regularization, can Obtain the model set. The deviation is the closest approximation to the true value that the elements can achieve. The larger the set, the smaller the deviation, and may be 0 (if).
However, the larger the set, the smaller the size of its members. The more samples in the range, the greater the variance of the algorithm output model. The overall generalization error is the sum of the bias and the variance. Therefore, statistical learning is usually a Bias-Variance trade-off, and the correct model complexity is to minimize the overall error. In fact, Geman et al. demonstrate their pessimism about neural networks by arguing that the fundamental limitations posed by the Bias-Variance dilemma apply to all nonparametric inference models, including neural networks.
"The more the merrier" is not Always true: In statistical learning, more features or data does not necessarily improve performance. For example, learning from data containing many irrelevant features is difficult. Similarly, learning from mixture models where the data Coming from one of two distributions (such as and , is harder than learning each distribution independently.
Diminishing Returns: In many cases, the number of data points required to reduce the prediction noise to level is the same as the parameter sum Relevant, that is, the number of data points is approximately equal to . In this case, approximately k samples are needed to get started, but once you do so, you face diminishing returns, i.e. if it takes k points to achieve 90% accuracy, approximately additional points are needed to increase accuracy to 95%. Generally speaking, as resources increase (whether data, model complexity, or computation), one hopes to obtain increasingly fine distinctions rather than unlocking specific New features.
Heavy dependence on loss, data: When fitting a model to high-dimensional data, any small detail can make a big difference. Choices like L1 or L2 regularizer Very important, let alone using completely different data sets. Different numbers of high-dimensional optimizers are also very different from each other.
The data is relatively "naive": it is usually assumed that the data is independent of some The distribution is sampled. Although points close to the decision boundary are difficult to classify, considering the phenomenon of measurement concentration in high dimensions, it can be considered that the distances of most points are similar. Therefore, in the classic data distribution, the distance between data points The difference is modest. However, mixed models can show this difference, so unlike the other problems above, this difference is common in statistics.
Scenario B: Learning Mathematics
In this scenario, we assume that you want to teach students mathematics (such as calculating derivatives) through some instructions and exercises. This scenario, although not formally defined, has some qualitative characteristics:

From improving capabilities to automated representation: Although there are also diminishing returns to problem solving in some cases, students learn through several stages. There is a stage where solving some problems helps understand the concepts and unlock new abilities. In addition, when students repeat a specific type of problem, they will form an automated problem-solving process when they see similar problems, transforming from previous ability improvement to automatic problem-solving.
Performance is independent of data and losses: There is more than one way to teach mathematical concepts. Students who study using different books, educational methods, or grading systems can end up learning the same content and have similar mathematical abilities.
Some problems are more difficult: In math exercises, we often see strong correlations between how different students solve the same problem. There does seem to be an inherent level of difficulty for a problem, and a natural progression of difficulty that is best for learning.
Deep learning is more about statistical estimation or student learning skills?
Of the two metaphors above, which one is more appropriate to describe modern deep learning? Specifically, what makes it successful? Statistical model fitting can be well expressed using mathematics and code. In fact, the canonical Pytorch training loop trains deep networks via empirical risk minimization:

At a deeper level, the relationship between these two scenarios is not clear. To be more specific, here is a specific learning task as an example. Consider a classification algorithm trained using the "self-supervised learning linear detection" method. The specific algorithm training is as follows:
1. Assume that the data is a sequence, where is a certain data point (such as a picture) and is the label.
is a certain data point (such as a picture) and is the label.
2. First get the deep neural network that represents the function  . A self-supervised loss function of some type is trained by minimizing it using only data points and not labels. Examples of such loss functions are reconstruction (restoring the input with other inputs) or contrastive learning (the core idea is to compare positive and negative samples in the feature space to learn the feature representation of the sample).
. A self-supervised loss function of some type is trained by minimizing it using only data points and not labels. Examples of such loss functions are reconstruction (restoring the input with other inputs) or contrastive learning (the core idea is to compare positive and negative samples in the feature space to learn the feature representation of the sample).
3. Fit a linear classifier  (which is the number of classes) using the complete labeled data to minimize the cross-entropy loss. Our final classifier is:
(which is the number of classes) using the complete labeled data to minimize the cross-entropy loss. Our final classifier is:

Step 3 only works for linear classifiers, so the "magic" happens in step 2 (self-supervised learning of deep networks). There are some important properties in self-supervised learning:
Learn a skill rather than approximating a function: Self-supervised learning is not about approximating a function, but about learning representations that can be used for a variety of downstream tasks (this is natural language processing dominant paradigm). Obtaining downstream tasks through linear probing, fine-tuning, or excitation is secondary.
The more the merrier: In self-supervised learning, the quality of representation improves as the amount of data increases and does not get worse by mixing data from several sources. In fact, the more diverse the data, the better.

Dataset of Coogle PaLM model
Unlock new capabilities: As the investment in resources (data, computing, model size) increases, the deep learning model also Improving discontinuously. This has also been demonstrated in some combination environments.

As model size increases, PaLM shows discrete improvements in benchmarks and unlocks surprising capabilities, like explaining why a joke is funny.
Performance is almost independent of loss or data: there are multiple self-supervised losses, a variety of contrast and reconstruction losses are actually used in image research, language models use single-sided reconstruction (predicting the next token) or use a mask model , predict the mask input from the left and right tokens. It is also possible to use slightly different data sets. These may impact efficiency, but as long as "reasonable" choices are made, often the original resource improves prediction performance more than the specific loss or dataset used.
Some cases are more difficult than others: this point is not specific to self-supervised learning. Data points seem to have some inherent "difficulty level". In fact, different learning algorithms have different "skill levels", and different data dians have different "difficulty levels" (the probability of a classifier correctly classifying a point increases monotonically with skill and decreases monotonically with difficulty).
The "skill vs. difficulty" paradigm is the clearest explanation of the "accuracy on the line" phenomenon discovered by Recht et al. and Miller et al. The paper by Kaplen, Ghosh, Garg, and Nakkiran also shows how different inputs in a data set have inherent "difficulty profiles" that are generally robust to different model families.

C** Accuracy on the line phenomenon for a classifier trained on IFAR-10 and tested on CINIC-10. Figure source: https://millerjohnp-linearfits-app-app-ryiwcq.streamlitapp.com/

The top figure depicts different softmax probabilities for the most likely class, as A function of the global accuracy of a classifier for a class indexed by training time. The bottom pie chart shows the decomposition of different data sets into different types of points (note that this decomposition is similar for different neural structures).
Training is teaching: The training of modern large models seems to be more like teaching students rather than letting the model fit the data. When students do not understand or feel tired, they "rest" or try different methods (training difference). Meta's large model training logs are instructive - in addition to hardware issues, we can also see interventions such as switching different optimization algorithms during training, and even considering "hot swapping" activation functions (GELU to RELU). The latter doesn't make much sense if you think of model training as fitting the data, rather than learning a representation.

Meta Training Log Excerpt
4.1 But what about supervised learning?
Self-supervised learning was discussed earlier, but the typical example of deep learning is still supervised learning. After all, deep learning’s “ImageNet moment” came from ImageNet. So does what was discussed above still apply to this setting?
First, the emergence of supervised large-scale deep learning was somewhat accidental, thanks to the availability of large, high-quality labeled datasets (i.e., ImageNet). If you have a good imagination, you can imagine an alternative history in which deep learning first started making breakthroughs in natural language processing through unsupervised learning, before moving to vision and supervised learning.
Secondly, there is evidence that supervised learning and self-supervised learning behave "internally" similarly despite using completely different loss functions. Both usually achieve the same performance. Specifically, for each, one can combine the first k layers of a model of depth d trained with self-supervision with the last d-k layers of the supervised model with little performance loss.

Table for SimCLR v2 paper. Note the general similarity in performance between supervised learning, fine-tuned (100%) self-supervised, and self-supervised linear detection (Source: https://arxiv.org/abs/2006.10029)

Splice the self-supervised model and Bansal et al.’s supervised model (https://arxiv.org/abs/2106.07682). Left: If the accuracy of the self-supervised model is (say) 3% lower than the supervised model, then a fully compatible representation will result in a splicing penalty of p 3% when p parts of the layer come from the self-supervised model. If the models are completely incompatible, then we would expect accuracy to drop dramatically as more models are merged. Right: Actual results combining different self-supervised models.
The advantage of self-supervised simple models is that they can combine feature learning or "deep learning magic" (done by deep representation functions) with statistical model fitting (represented here by linear or other "simple" classifiers completed above) separation.
Finally, although this is more of a speculation, the fact is that "meta-learning" often seems to be equated with learning representations (see: https://arxiv.org/abs/1909.09157, https://arxiv .org/abs/2206.03271), which can be seen as another evidence that this is largely done regardless of the goals of model optimization.
4.2 What to do about over-parameterization?
This article skips what are considered to be classic examples of differences between statistical learning models and deep learning in practice: the lack of “Bias-Variance trade-off” and the ability of over-parameterized models to generalize well.
Why skip? There are two reasons:
- First, if supervised learning is indeed equivalent to self-supervised simple learning, then this may explain its generalization ability.
- Secondly, over-parameterization is not the key to the success of deep learning. What makes deep networks special is not that they are large compared to the number of samples, but that they are large in absolute terms. In fact, usually in unsupervised/self-supervised learning, the model is not over-parameterized. Even for very large language models, their datasets are larger.

Nakkiran-Neyshabur-Sadghi "deep bootstrap" paper shows that modern architectures behave similarly in "over-parameterized" or "under-sampled" regimes (models in Training for multiple epochs on limited data until overfitting: the "Real World" in the figure above), also in the "under-parameterized" or "online" state (the model is trained for a single epoch, and each sample is only viewed once: "Ideal World" pictured above). Figure source: https://arxiv.org/abs/2010.08127
Summary
Statistical learning certainly plays a role in deep learning. However, despite using similar terminology and code, viewing deep learning as simply fitting a model with more parameters than a classical model ignores much that is critical to its success. The metaphor for teaching students mathematics is not perfect either.
Like biological evolution, although deep learning contains many reused rules (such as gradient descent with experience loss), it can produce highly complex results. It seems that at different times, different components of the network learn different things, including representation learning, predictive fitting, implicit regularization, and pure noise. Researchers are still looking for the right lens to ask questions about deep learning, let alone answer them.
The above is the detailed content of Learning = fitting? Are deep learning and classic statistics the same thing?. For more information, please follow other related articles on the PHP Chinese website!
 Personal Hacking Will Be A Pretty Fierce BearMay 11, 2025 am 11:09 AM
Personal Hacking Will Be A Pretty Fierce BearMay 11, 2025 am 11:09 AMCyberattacks are evolving. Gone are the days of generic phishing emails. The future of cybercrime is hyper-personalized, leveraging readily available online data and AI to craft highly targeted attacks. Imagine a scammer who knows your job, your f
 Pope Leo XIV Reveals How AI Influenced His Name ChoiceMay 11, 2025 am 11:07 AM
Pope Leo XIV Reveals How AI Influenced His Name ChoiceMay 11, 2025 am 11:07 AMIn his inaugural address to the College of Cardinals, Chicago-born Robert Francis Prevost, the newly elected Pope Leo XIV, discussed the influence of his namesake, Pope Leo XIII, whose papacy (1878-1903) coincided with the dawn of the automobile and
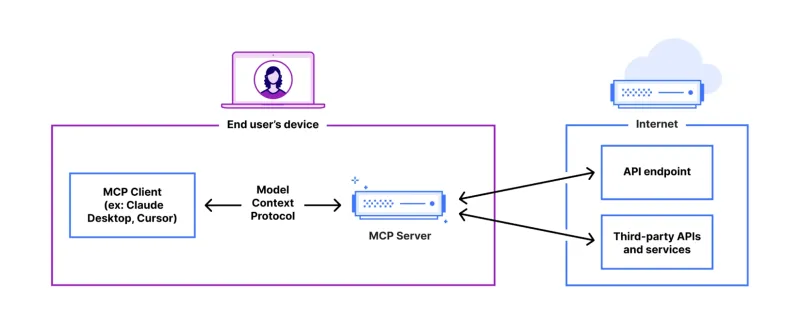 FastAPI-MCP Tutorial for Beginners and Experts - Analytics VidhyaMay 11, 2025 am 10:56 AM
FastAPI-MCP Tutorial for Beginners and Experts - Analytics VidhyaMay 11, 2025 am 10:56 AMThis tutorial demonstrates how to integrate your Large Language Model (LLM) with external tools using the Model Context Protocol (MCP) and FastAPI. We'll build a simple web application using FastAPI and convert it into an MCP server, enabling your L
 Dia-1.6B TTS : Best Text-to-Dialogue Generation Model - Analytics VidhyaMay 11, 2025 am 10:27 AM
Dia-1.6B TTS : Best Text-to-Dialogue Generation Model - Analytics VidhyaMay 11, 2025 am 10:27 AMExplore Dia-1.6B: A groundbreaking text-to-speech model developed by two undergraduates with zero funding! This 1.6 billion parameter model generates remarkably realistic speech, including nonverbal cues like laughter and sneezes. This article guide
 3 Ways AI Can Make Mentorship More Meaningful Than EverMay 10, 2025 am 11:17 AM
3 Ways AI Can Make Mentorship More Meaningful Than EverMay 10, 2025 am 11:17 AMI wholeheartedly agree. My success is inextricably linked to the guidance of my mentors. Their insights, particularly regarding business management, formed the bedrock of my beliefs and practices. This experience underscores my commitment to mentor
 AI Unearths New Potential In The Mining IndustryMay 10, 2025 am 11:16 AM
AI Unearths New Potential In The Mining IndustryMay 10, 2025 am 11:16 AMAI Enhanced Mining Equipment The mining operation environment is harsh and dangerous. Artificial intelligence systems help improve overall efficiency and security by removing humans from the most dangerous environments and enhancing human capabilities. Artificial intelligence is increasingly used to power autonomous trucks, drills and loaders used in mining operations. These AI-powered vehicles can operate accurately in hazardous environments, thereby increasing safety and productivity. Some companies have developed autonomous mining vehicles for large-scale mining operations. Equipment operating in challenging environments requires ongoing maintenance. However, maintenance can keep critical devices offline and consume resources. More precise maintenance means increased uptime for expensive and necessary equipment and significant cost savings. AI-driven
 Why AI Agents Will Trigger The Biggest Workplace Revolution In 25 YearsMay 10, 2025 am 11:15 AM
Why AI Agents Will Trigger The Biggest Workplace Revolution In 25 YearsMay 10, 2025 am 11:15 AMMarc Benioff, Salesforce CEO, predicts a monumental workplace revolution driven by AI agents, a transformation already underway within Salesforce and its client base. He envisions a shift from traditional markets to a vastly larger market focused on
 AI HR Is Going To Rock Our Worlds As AI Adoption SoarsMay 10, 2025 am 11:14 AM
AI HR Is Going To Rock Our Worlds As AI Adoption SoarsMay 10, 2025 am 11:14 AMThe Rise of AI in HR: Navigating a Workforce with Robot Colleagues The integration of AI into human resources (HR) is no longer a futuristic concept; it's rapidly becoming the new reality. This shift impacts both HR professionals and employees, dem


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

SublimeText3 Linux new version
SublimeText3 Linux latest version

WebStorm Mac version
Useful JavaScript development tools






