In 1994, a mathematician figured out how to make quantum computers do things that ordinary classical computers cannot. The work shows that, in principle, a machine based on the rules of quantum mechanics can efficiently decompose large numbers into their principal factors - a very difficult task for classical computers, which make up most of today's Fundamentals of Internet Security.
#With it came a wave of optimism. Perhaps, researchers believe, we will be able to invent quantum algorithms that can solve a large number of different problems.
#But progress has stalled. "It's kind of disappointing," said Ryan O'Donnell of Carnegie Mellon University. "People are going to say, 'This is great, I'm sure we're going to get all kinds of other amazing algorithms,' and they're not." The scientists only found significant speedups for a single, narrow class of problems in a standard set called NP, meaning they have efficient verifiable solutions - such as factorization.
This has been the case for the past three years. Then in April, researchers invented an entirely new kind of problem that quantum computers should be able to solve faster than classical computers. It involves calculating the input of a complex mathematical process based only on its messy output. Whether this problem stands alone or is the first of many others remains to be determined.
"There is a sense of excitement," said Vinod Vaikuntanathan, a computer scientist at MIT. "A lot of people are thinking about what else is out there."
Computer scientists try to understand what quantum computers do better by studying the mathematical models that represent them. Typically, they imagine a model of a quantum or classical computer paired with an ideal computer called an oracle. An oracle is like a simple mathematical function or computer program that takes input and outputs a predetermined output.
They may have random behavior, outputting "yes" if the input is within some random range (for example, 12 to 67) and "no" otherwise. Or they might be periodic, so input between 1 and 10 returns "yes", 11 to 20 produces "no", 21 to 30 again produces "yes", and so on.
#Suppose you have one of these periodic prophecies, but you don't know the period. All you can do is feed it numbers and see what it outputs. How fast can a computer find cycles under these constraints? In 1993, Daniel Simon, then at the University of Montreal, discovered that quantum algorithms could compute answers to closely related problems faster than any classical algorithm.

This result allowed Simon to identify one of the first signs of where quantum computers would have significant advantages. But when he submitted his paper to a major conference, it was rejected. The paper did, however, pique the interest of a junior member of the conference program committee, Peter Shor, who was then working at Bell Laboratories in New Jersey.
Shor went on to discover that he could tweak Simon's algorithm to calculate the period of the oracle, if it had one. Then he realized he could tweak the algorithm again to solve an equation that behaved like a periodic prophecy: an equation describing factorization that was periodic.
Shor’s results were historic. The quantum algorithm he discovered can quickly reduce huge numbers to their constituent prime factors, something no known classical algorithm can do. In subsequent years, researchers discovered other efficient quantum algorithms. Some of them, like Shor's algorithm, even provide exponential advantages, but no one has been able to prove a significant quantum advantage on any non-periodic NP problem.
#The lack of progress prompted two computer scientists, Scott Aaronson of the University of Texas at Austin and Andris Ambainis of the University of Latvia, to observe. Proofs of quantum advantage always seem to rely on predictions with some non-random structure, such as periodicity. In 2009, they speculated that there would be no significant speedup for random or unstructured NP problems; no one could find exceptions.
Their conjectures limit the capabilities of quantum computers. But it only says that for certain types of unstructured NP problems—those with yes or no answers—there is no significant speedup. This conjecture does not apply if a problem involves finding a more specific, quantitative answer, a so-called search problem.
With this in mind, researchers Takashi Yamakawa of NTT's Social Informatics Laboratory and Mark Zhandry of NTT Research and Princeton University decided to investigate a project developed by Oded Regev in Experiment with specific search questions posed in 2005.
#Imagine a set of weathervanes that all point in the same direction. Give them each a measured push and let the gust influence their direction. Regev wants to determine where they were originally pointed based on their final direction. Problems like this came to be known as "error learning" because thrust and wind act as random sources of error in the original direction. There is evidence that both classical and quantum algorithms are difficult to solve.
Yamakawa and Zhandry tweaked the settings. They modified the power of these starts to make them more predictable. They also made the wind determined by a random oracle, so in some cases it's even more random, but in other cases completely dormant.
#With these modifications, the researchers found that the quantum algorithm could effectively find the initial direction. They also proved that any classical algorithm must be slowed down by an exponential factor. Like Shor, they then adapted the algorithm to solve a realistic version of the problem, replacing the predictions with actual mathematical equations.
Computer scientists are still trying to understand and solve this problem. Vaikuntanathan compared this to a different situation that occurs when doing data compression: when information is compressed, two bits can accidentally squeeze into the same place, thus overwriting them. The problems of anticipating these collisions in advance so as to avoid them have some similarities. "This is a class of problems that basically look like this," he said. "Maybe these problems can be solved quantumly."
People hope, Even on today's fledgling versions of quantum computers, unstructured problems like novel problems can be solved, providing a way to test them. The idea was that unstructured problems might require fewer resources to program or be less sensitive to noise because they are already random. But so far, this new problem still seems too advanced for existing quantum computers to solve. "It's a weird question. I didn't think about defining it," Aaronson said, "but in retrospect, it has some really nice features."
This result provides the first example of significant quantum advantage on an unstructured NP problem. Will many other problems in the quantum world go from being nearly unsolvable to solvable? Now there are even more reasons to think so. “This to some extent changes our view of what problems quantum computers are good at solving,” O’Donnell said.
The above is the detailed content of Quantum algorithms conquer a new kind of problem!. For more information, please follow other related articles on the PHP Chinese website!
 What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AM
What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AMIntroduction In prompt engineering, “Graph of Thought” refers to a novel approach that uses graph theory to structure and guide AI’s reasoning process. Unlike traditional methods, which often involve linear s
 Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AM
Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AMIntroduction Congratulations! You run a successful business. Through your web pages, social media campaigns, webinars, conferences, free resources, and other sources, you collect 5000 email IDs daily. The next obvious step is
 Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AM
Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AMIntroduction In today’s fast-paced software development environment, ensuring optimal application performance is crucial. Monitoring real-time metrics such as response times, error rates, and resource utilization can help main
 ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM
ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM“How many users do you have?” he prodded. “I think the last time we said was 500 million weekly actives, and it is growing very rapidly,” replied Altman. “You told me that it like doubled in just a few weeks,” Anderson continued. “I said that priv
 Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AM
Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AMIntroduction Mistral has released its very first multimodal model, namely the Pixtral-12B-2409. This model is built upon Mistral’s 12 Billion parameter, Nemo 12B. What sets this model apart? It can now take both images and tex
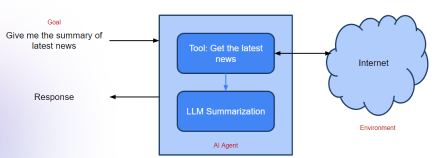 Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AM
Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AMImagine having an AI-powered assistant that not only responds to your queries but also autonomously gathers information, executes tasks, and even handles multiple types of data—text, images, and code. Sounds futuristic? In this a
 Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AM
Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AMIntroduction The finance industry is the cornerstone of any country’s development, as it drives economic growth by facilitating efficient transactions and credit availability. The ease with which transactions occur and credit
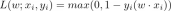 Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AM
Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AMIntroduction Data is being generated at an unprecedented rate from sources such as social media, financial transactions, and e-commerce platforms. Handling this continuous stream of information is a challenge, but it offers an


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

SublimeText3 Chinese version
Chinese version, very easy to use

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

Dreamweaver Mac version
Visual web development tools

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.





