Home >Backend Development >Python Tutorial >Use Python to implement RSA encryption and decryption
Use Python to implement RSA encryption and decryption
- 王林forward
- 2023-04-14 14:13:033328browse
I saw an English article [1] yesterday, showing how to use Python to implement the RSA algorithm. The logic of the code is the same as the previous article Understanding the RSA Algorithm. Friends who are not familiar with RSA can read the article Understanding the RSA Algorithm. , which explains what RSA is, the mathematical principles of RSA, and gives a simple example. It can be said to be the easiest article to understand RSA on Quanzhihu (this comes from a reader's comment).
I ran the code provided in English and found that it could not encrypt Chinese, so I modified the encryption and decryption functions to support Chinese encryption and decryption. Today’s article will share how to use Python to implement the RSA encryption and decryption process to help you establish an intuitive understanding of RSA. The random prime number generation algorithm in the code is also worth learning.
0. Effect demonstration
Let’s take a look at the effect first.
Original text: "There is a mole, terminate the transaction"
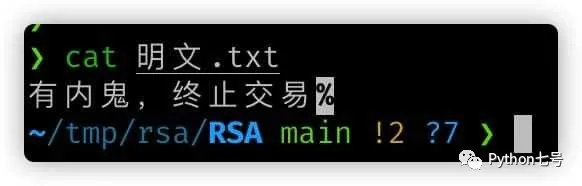
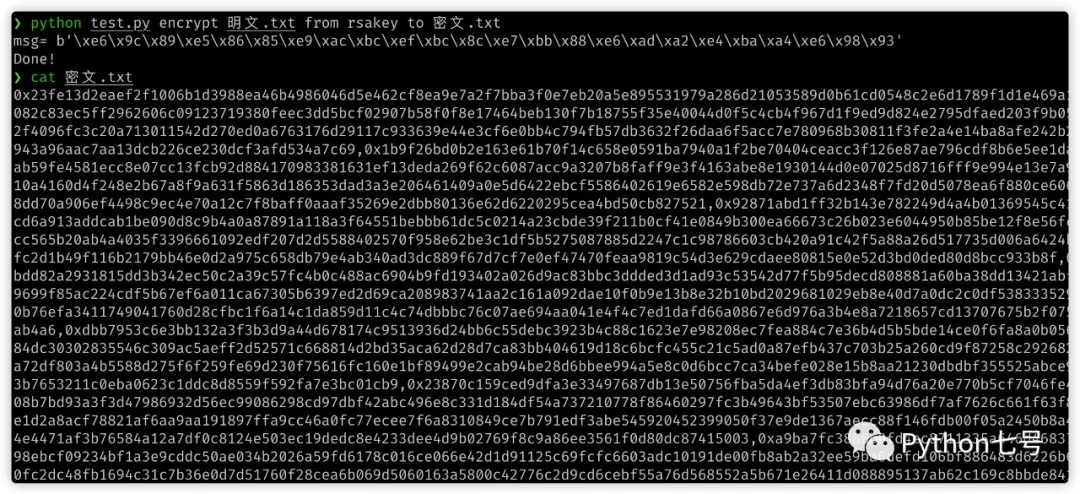
The cipher text cannot be cracked at all:
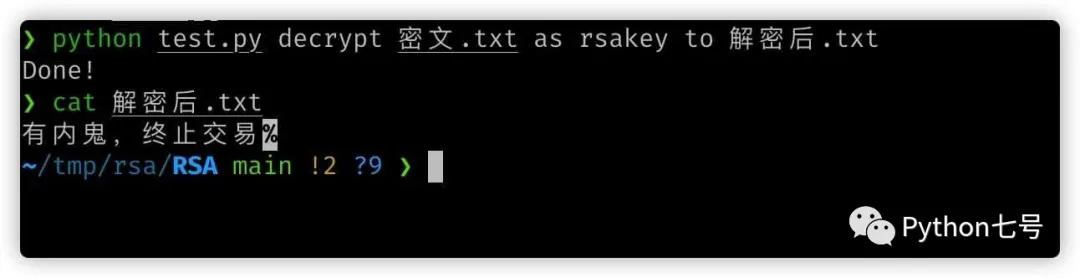
After decryption:
The complete code public account "Python No. 7" can be obtained by replying "rsa".
1. Key pair generation
Ideas:
1) Randomly find two prime numbers (prime numbers) p and q. The larger p and q, the safer they are. Here we choose a 1024-bit prime number:
p = genprime(1024) q = genprime(1024)
genprime() Let’s not talk about the implementation process of the function.
2) Calculate their product n = p * q and Euler function lambda_n.
n = p * q lambda_n = (p - 1) * (q - 1)
3) Randomly select an integer e, the condition is 1
e = 35537
4) Find an integer d such that the remainder of e * d divided by lambda_n is 1, and return the key pair.
d = eucalg(e, lambda_n)[0] if d < 0: d += lambda_n return (d, n), (e, n)
The implementation of the eucalg function will be discussed later.
At this point, the key pair generation function is as follows:
def create_keys(): p = genprime(1024) q = genprime(1024) n = p * q lambda_n = (p - 1) * (q - 1) e = 35537 d = eucalg(e, lambda_n)[0] if d < 0: d += lambda_n return (d, n), (e, n)
2. Implementation of encryption and decryption
The encryption and decryption processes are the same, public key encryption, private key encryption Key decryption, and vice versa, private key encryption and public key decryption, but the former is called encryption and the latter is called signature.
The specific function implementation is as follows:
def encrypt_data(data,key): e_data = [] for d in data: e = modpow(d, key[0], key[1]) e_data.append(e) return e_data ## 加密和解密的逻辑完全一样 decrypt_data = encrypt_data
The modpow function is used here, which is used to calculate the formula b^e % n = r.
- If it is an encryption process, then b is the plaintext, (n,e) is the public key, and r is the ciphertext.
- If it is a decryption process, then b is the ciphertext, (n, d) is the private key, and r is the famous text.
modpow is defined as follows:
def modpow(b, e, n): # find length of e in bits tst = 1 siz = 0 while e >= tst: tst <<= 1 siz += 1 siz -= 1 # calculate the result r = 1 for i in range(siz, -1, -1): r = (r * r) % n if (e >> i) & 1: r = (r * b) % n return r
3. Generating function of random prime numbers
Generating function of random prime numbers, which uses matrix multiplication and Fibonacci Sequence shows the importance of mathematics to algorithms.
# matrix multiplication def sqmatrixmul(m1, m2, w, mod): mr = [[0 for j in range(w)] for i in range(w)] for i in range(w): for j in range(w): for k in range(w): mr[i][j] = (mr[i][j] + m1[i][k] * m2[k][j]) % mod return mr # fibonacci calculator def fib(x, mod): if x < 3: return 1 x -= 2 # find length of e in bits tst = 1 siz = 0 while x >= tst: tst <<= 1 siz += 1 siz -= 1 # calculate the matrix fm = [ # function matrix [0, 1], [1, 1] ] rm = [ # result matrix # (identity) [1, 0], [0, 1] ] for i in range(siz, -1, -1): rm = sqmatrixmul(rm, rm, 2, mod) if (x >> i) & 1: rm = sqmatrixmul(rm, fm, 2, mod) # second row of resulting vector is result return (rm[1][0] + rm[1][1]) % mod def genprime(siz): while True: num = (1 << (siz - 1)) + secrets.randbits(siz - 1) - 10; # num must be 3 or 7 (mod 10) num -= num % 10 num += 3 # 3 (mod 10) # heuristic test if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0: return num num += 5 # 7 (mod 10) # heuristic test if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0: return num
4. Implementation of eucalg function
The essence of the function is to find the solution to the following linear equation of two variables:
e * x - lambda_n * y =1
Specific code:
def eucalg(a, b): # make a the bigger one and b the lesser one swapped = False if a < b: a, b = b, a swapped = True # ca and cb store current a and b in form of # coefficients with initial a and b # a' = ca[0] * a + ca[1] * b # b' = cb[0] * a + cb[1] * b ca = (1, 0) cb = (0, 1) while b != 0: # k denotes how many times number b # can be substracted from a k = a // b # swap a and b so b is always the lesser one a, b, ca, cb = b, a-b*k, cb, (ca[0]-k*cb[0], ca[1]-k*cb[1]) if swapped: return (ca[1], ca[0]) else: return ca
5 , test
test.py script usage method:
1), generate key
python test.py make-keys rsakey
The public key is saved in rsakey.pub, and the private key is saved in rsakey.priv中
2), Encrypt the file content
If there is a plain text .txt file:
python test.py encrypt 明文.txt from rsakey to 密文.txt
will generate a ciphertext .txt
3. Encrypt the file Content decryption
If there is a file ciphertext.txt:
python test.py decrypt 密文.txt as rsakey to 解密后.txt
will generate a decrypted .txt
Final words
This article shares the Python of the RSA algorithm A simple implementation can help understand the RSA algorithm.
The above is the detailed content of Use Python to implement RSA encryption and decryption. For more information, please follow other related articles on the PHP Chinese website!

