Why is mysql index fast?

The index is sorted in advance, so that high-efficiency algorithms such as binary search can be applied when searching. The complexity of general sequential search is O(n), while the complexity of binary search is O(log2n); when n is very large, the efficiency difference between the two is huge.

The operating environment of this tutorial: windows7 system, mysql8 version, Dell G3 computer.

Mysql is a very popular database on the Internet. The design of its underlying storage engine and data retrieval engine is very important. In particular, the storage form of Mysql data and the design of the index determine the overall data retrieval performance of Mysql.

We know that the function of an index is to quickly retrieve data, and the essence of fast retrieval is the data structure. Through the selection of different data structures, various data can be quickly retrieved. In the database, efficient search algorithms are very important, because a large amount of data is stored in the database, and an efficient index can save huge time. For example, in the following data table, if Mysql does not implement the index algorithm, then to find the data with id=7, you can only use violent sequential traversal to find the data. To find the data with id=7, you need to compare it 7 times. If this table stores 10 million pieces of data To search for the data with id=1000W, it will be compared 1000W times. This speed is unacceptable.

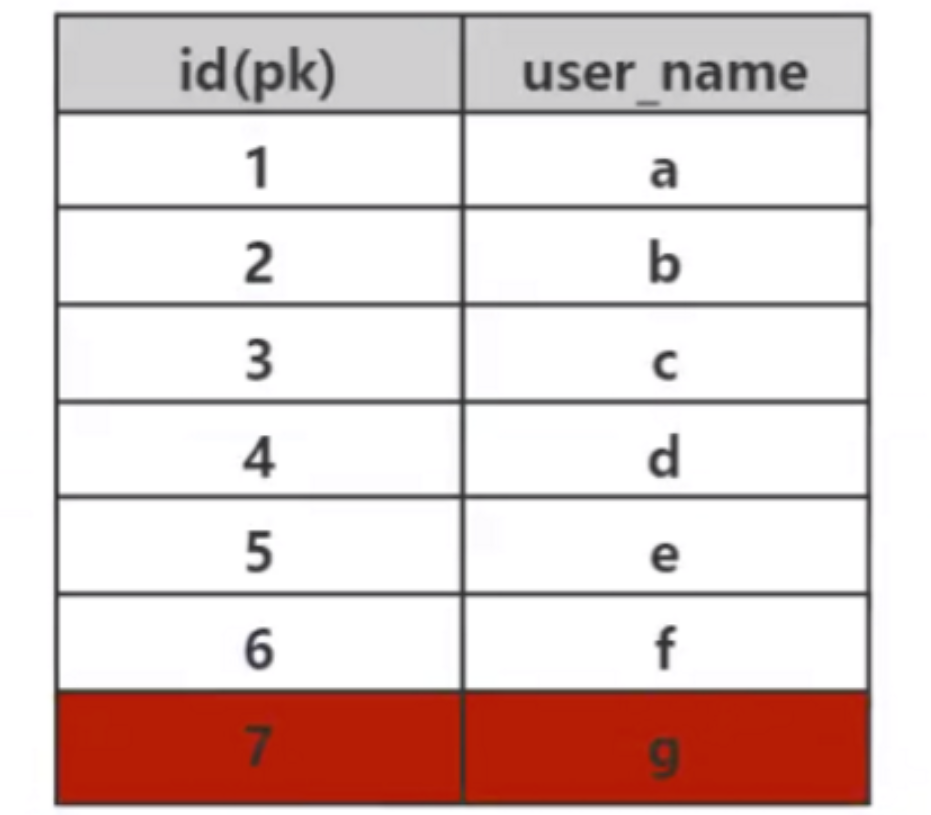
##1. Mysql index underlying data structure selection

Hash table (Hash)

Hash table is an effective tool for fast data retrieval.

Hash algorithm: Also called hash algorithm, it converts any value (key) into a fixed-length key address through a hash function, and uses this address to create a data structure for specific data.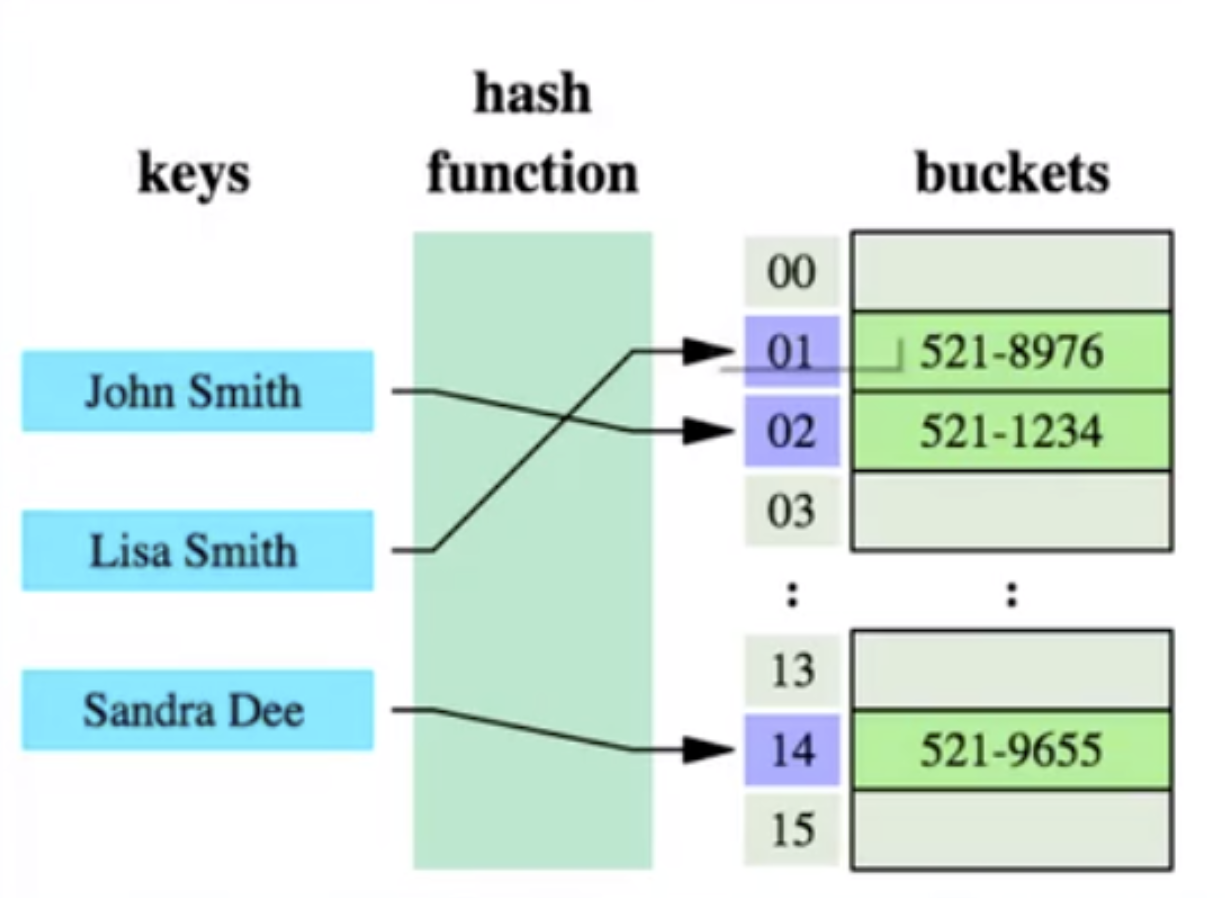

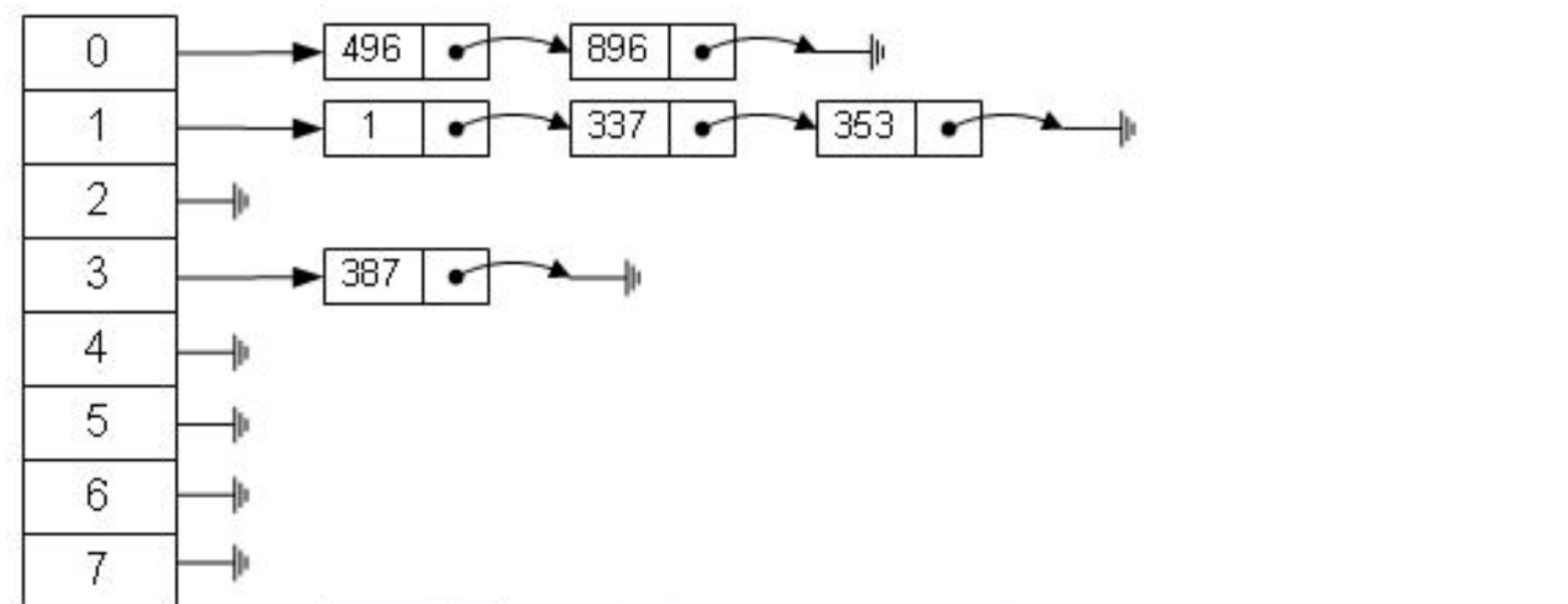
Consider this database table user. There are 7 data in the table. We need to retrieve the data with id=7. The SQL syntax is:

select * from user where id=7;

The hash algorithm first calculates the physical address addr=hash(7)=4231 to store the data with id=7, and the physical address mapped by 4231 is 0x77, and 0x77 is where id=7 is stored. The physical address of the data. The data corresponding to user_name='g' can be found through this independent address. This is the calculation process used by the hash algorithm to quickly retrieve data.

But the hash algorithm has a data collision problem, that is, the hash function may calculate the same result for different keys. For example, hash(7) may calculate the same result as hash(199). That is, different keys are mapped to the same result. This is a collision problem. A common way to solve the collision problem is the chain address method, which uses a linked list to connect the colliding data. After calculating the hash value, you also need to check whether the hash value has a collision in the data linked list. If so, it will be traversed to the end of the linked list until the data corresponding to the real key is found.

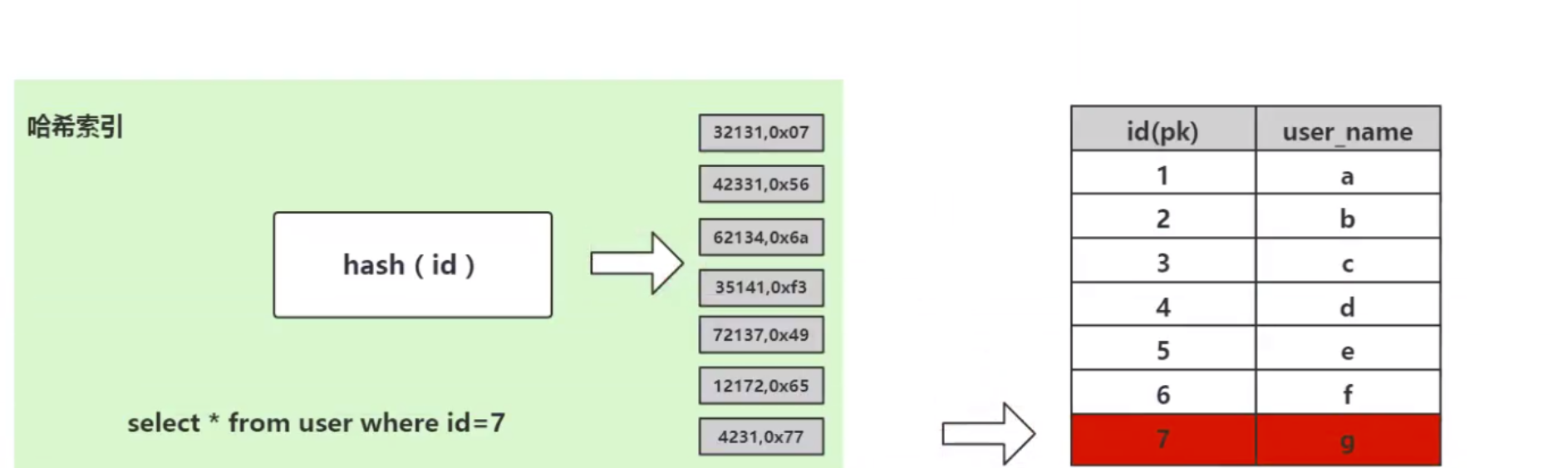
从算法时间复杂度分析来看，哈希算法时间复杂度为 O（1），检索速度非常快。比如查找 id=7 的数据，哈希索引只需要计算一次就可以获取到对应的数据，检索速度非常快。但是 Mysql 并没有采取哈希作为其底层算法，这是为什么呢？

因为考虑到数据检索有一个常用手段就是范围查找，比如以下这个 SQL 语句：

select * from user where id \>3;

针对以上这个语句，我们希望做的是找出 id>3 的数据，这是很典型的范围查找。如果使用哈希算法实现的索引，范围查找怎么做呢？一个简单的思路就是一次把所有数据找出来加载到内存，然后再在内存里筛选筛选目标范围内的数据。但是这个范围查找的方法也太笨重了，没有一点效率而言。

所以，使用哈希算法实现的索引虽然可以做到快速检索数据，但是没办法做数据高效范围查找，因此哈希索引是不适合作为 Mysql 的底层索引的数据结构。

二叉查找树(BST)

二叉查找树是一种支持数据快速查找的数据结构，如图下所示:

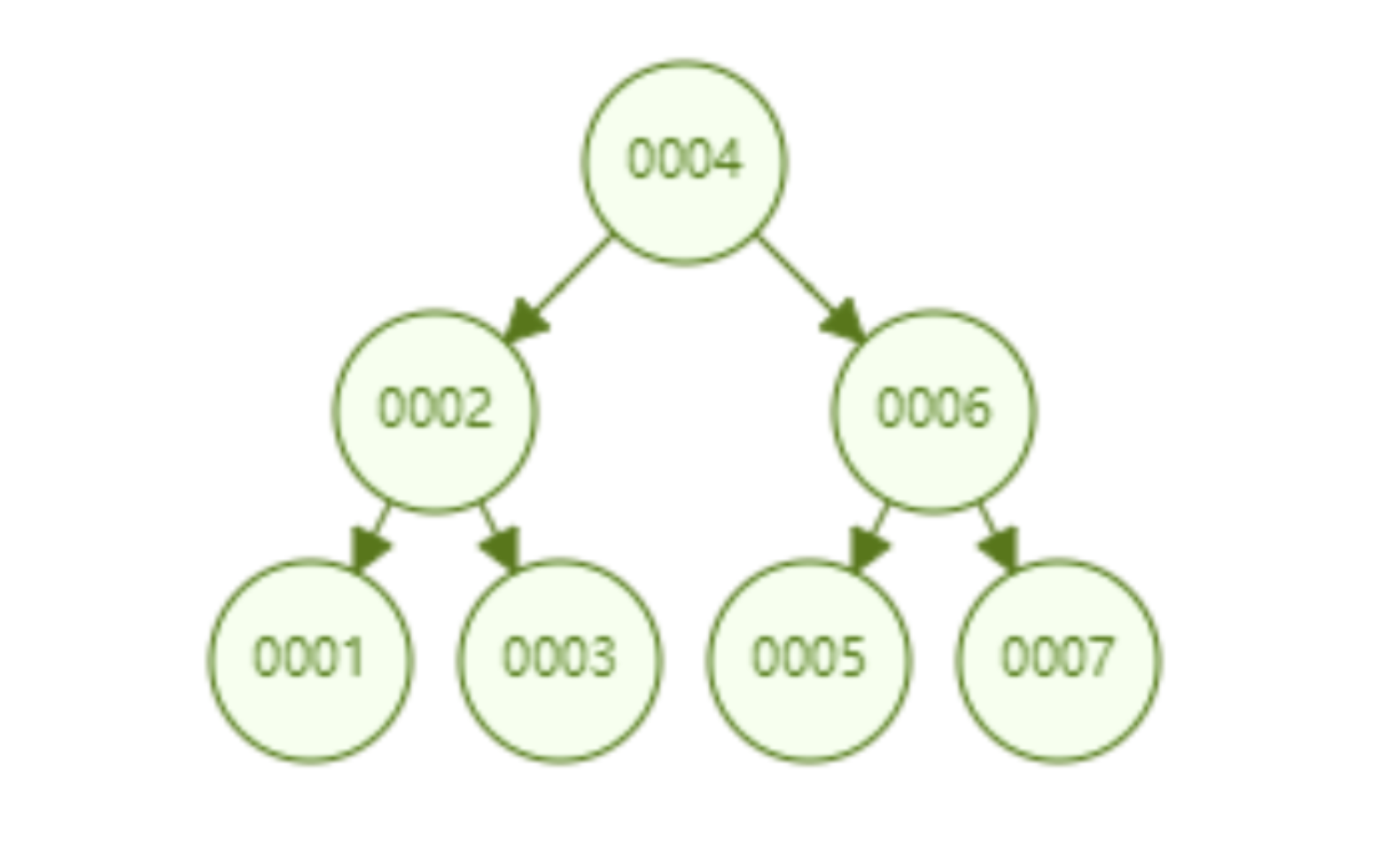
二叉查找树的时间复杂度是 O(lgn)，比如针对上面这个二叉树结构，我们需要计算比较 3 次就可以检索到 id=7 的数据，相对于直接遍历查询省了一半的时间，从检索效率上看来是能做到高速检索的。此外二叉树的结构能不能解决哈希索引不能提供的范围查找功能呢？

答案是可以的。观察上面的图，二叉树的叶子节点都是按序排列的，从左到右依次升序排列，如果我们需要找 id>5 的数据，那我们取出节点为 6 的节点以及其右子树就可以了，范围查找也算是比较容易实现。

但是普通的二叉查找树有个致命缺点：极端情况下会退化为线性链表，二分查找也会退化为遍历查找，时间复杂退化为 O（N），检索性能急剧下降。比如以下这个情况，二叉树已经极度不平衡了，已经退化为链表了，检索速度大大降低。此时检索 id=7 的数据的所需要计算的次数已经变为 7 了。

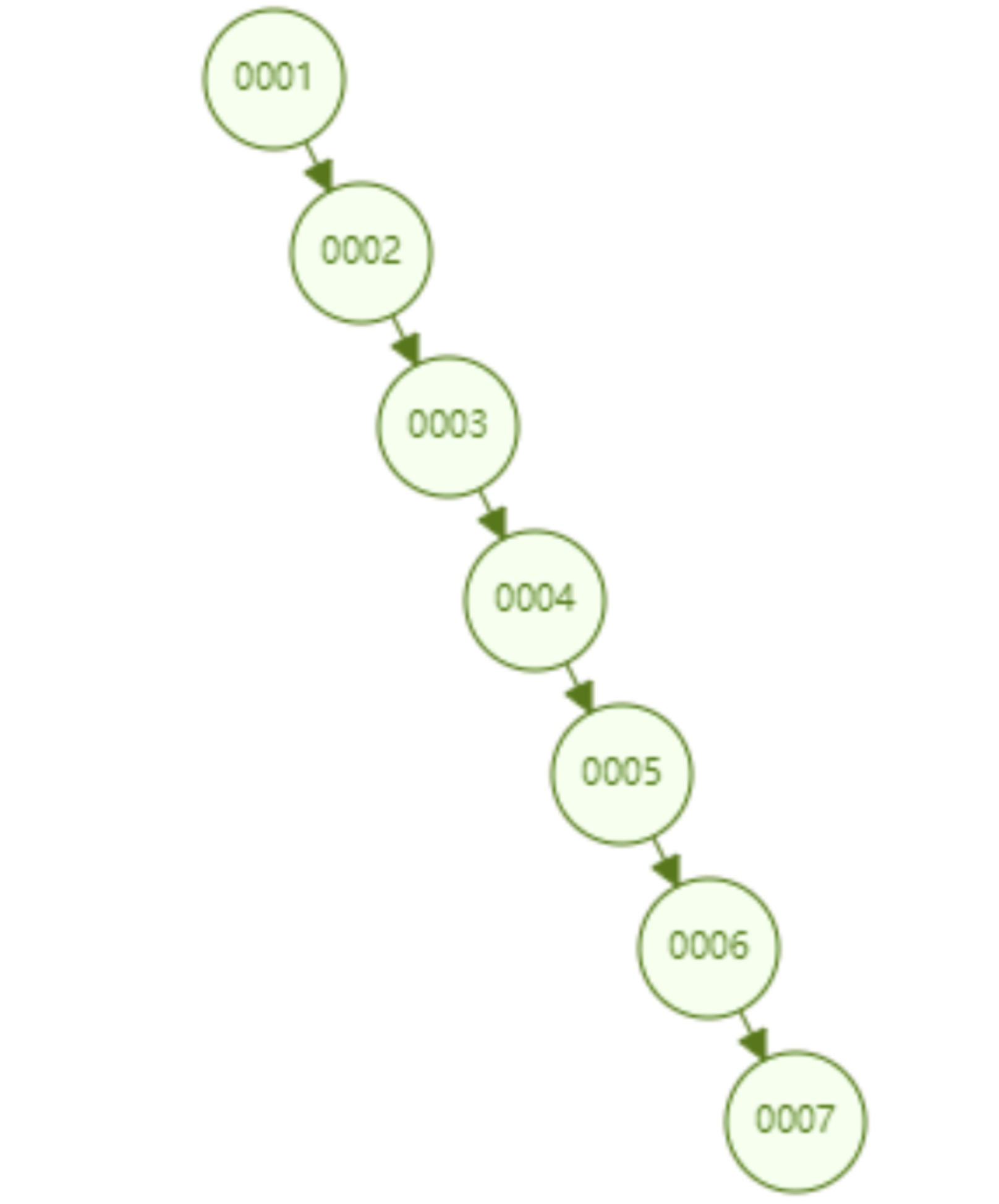
In the database, data auto-increment is a very common form. For example, the primary key of a table is id, and the primary key generally defaults to Self-increasing, if a data structure such as a binary tree is used as an index, then the linear search problem caused by the unbalanced state introduced above will inevitably occur. Therefore, a simple binary search tree has the problem of reduced retrieval performance caused by imbalance, and cannot be directly used to implement the underlying index of Mysql.

AVL tree and red-black tree

There is an imbalance problem in binary search trees, so scholars have proposed automatic By rotating and adjusting to keep the binary tree in a basically balanced state, you can maintain the best search performance of the binary search tree. Binary trees with self-adjusting equilibrium states based on this idea include AVL trees and red-black trees.

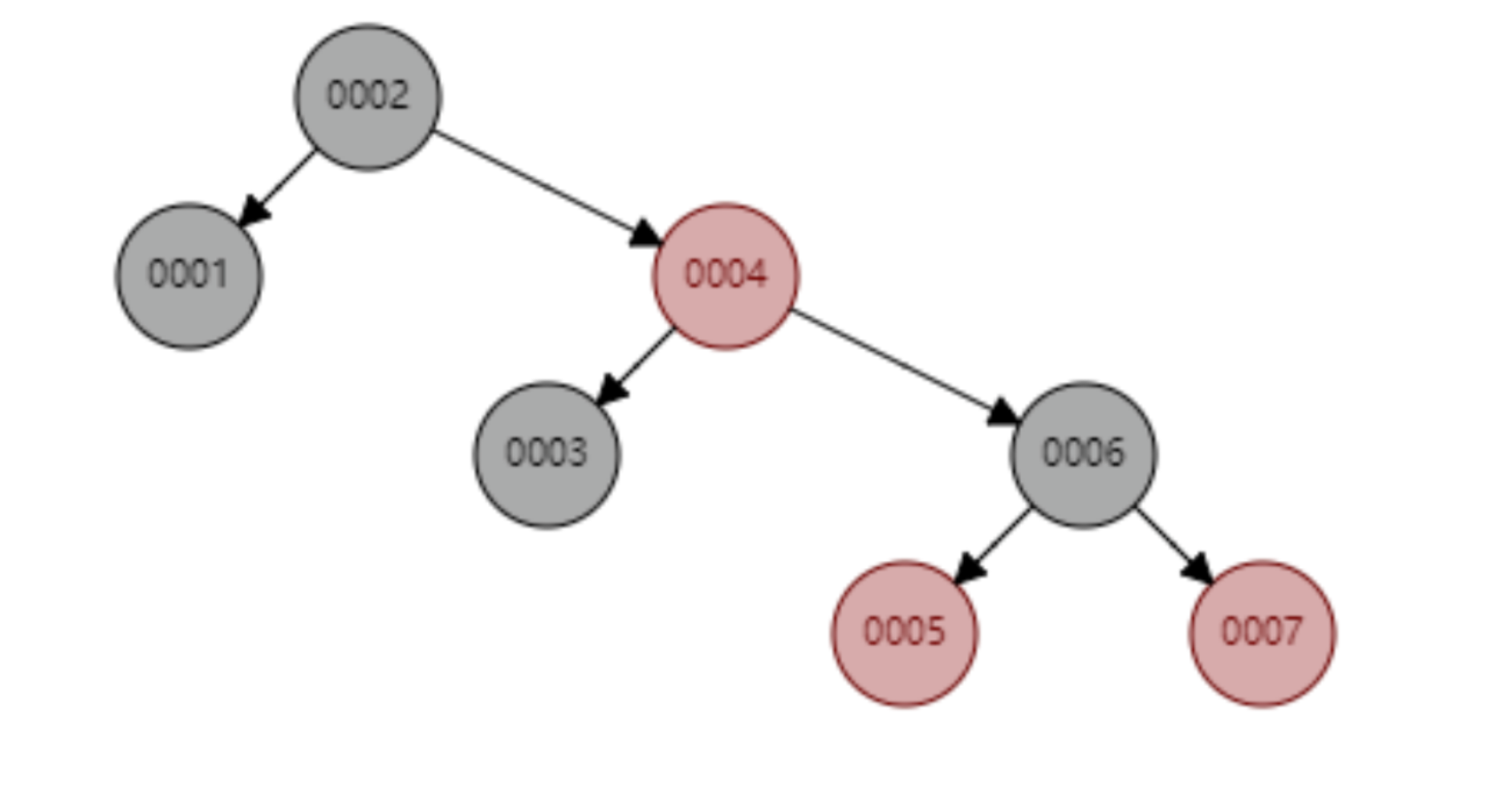
First of all, we briefly introduce the red-black tree. This is a tree structure that automatically adjusts the tree shape. For example, when the binary tree is in an unbalanced state, the red-black tree will automatically rotate left-right nodes and the nodes will change color. Adjusting the shape of the tree to maintain a basic balanced state (time complexity is O(logn)) ensures that the search efficiency will not be significantly reduced. For example, if data nodes are inserted in ascending order from 1 to 7, an ordinary binary search tree will degenerate into a linked list, but a red-black tree will continuously adjust the shape of the tree to maintain a basic balance, as shown in the figure below. The number of nodes to be compared when searching for id=7 in the red-black tree below is 4, which still maintains the good search efficiency of the binary tree.

The red-black tree has good average search efficiency, and there is no extreme O(n) situation. Can the red-black tree be used as the underlying index implementation of Mysql? In fact, red-black trees also have some problems. Look at the following example.
The red-black tree inserts 1~7 nodes sequentially, and the number of nodes that need to be calculated when searching for id=7 is 4.

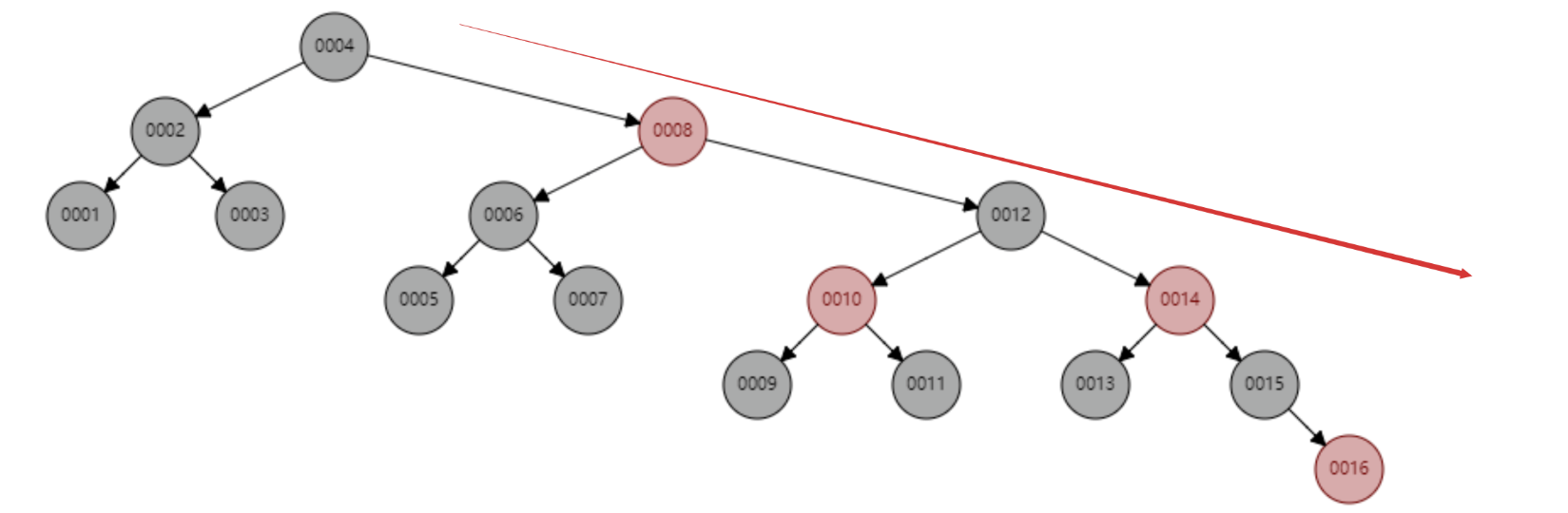
The red-black tree inserts 1~16 nodes sequentially, and the number of nodes that need to be compared when searching for id=16 is 6 times . Observe the shape of this tree. Is it true that when data is inserted sequentially, the shape of the tree has always been in a "right-leaning" trend? Fundamentally, the red-black tree does not completely solve the binary search tree. Although this "right-leaning" trend is far less exaggerated than the binary search tree degenerating into a linear linked list, the basic primary key auto-increment operation in the database, the primary key is generally Millions and tens of millions. If the red-black tree has this kind of problem, it will also consume a huge amount of search performance. Our database cannot tolerate this meaningless waiting.

Now consider another more strict self-balancing binary tree, the AVL tree. Because the AVL tree is an absolutely balanced binary tree, it consumes more performance in adjusting the shape of the binary tree.

AVL tree inserts 1~7 nodes sequentially, and the number of times to compare the node with id=7 is 3.

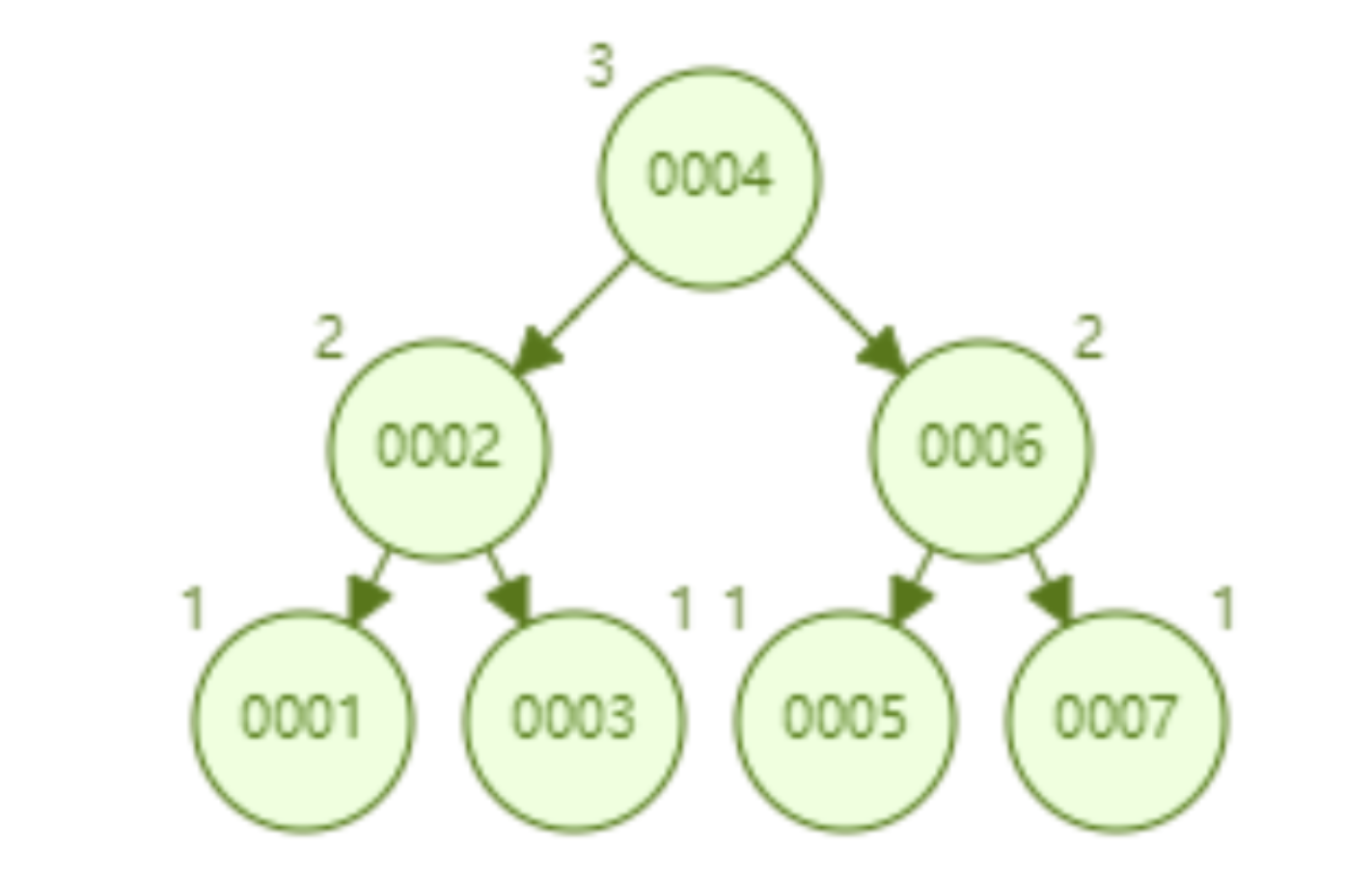
AVL tree sequentially inserts 1~16 nodes, and the number of nodes to be compared when searching for id=16 is 4. In terms of search efficiency, the search speed of AVL tree is higher than that of red-black tree (AVL tree is 4 comparisons, red-black tree is 6 comparisons). Judging from the shape of the tree, AVL trees do not have the "right leaning" problem of red-black trees. In other words, a large number of sequential insertions will not lead to a decrease in query performance, which fundamentally solves the problem of red-black trees.

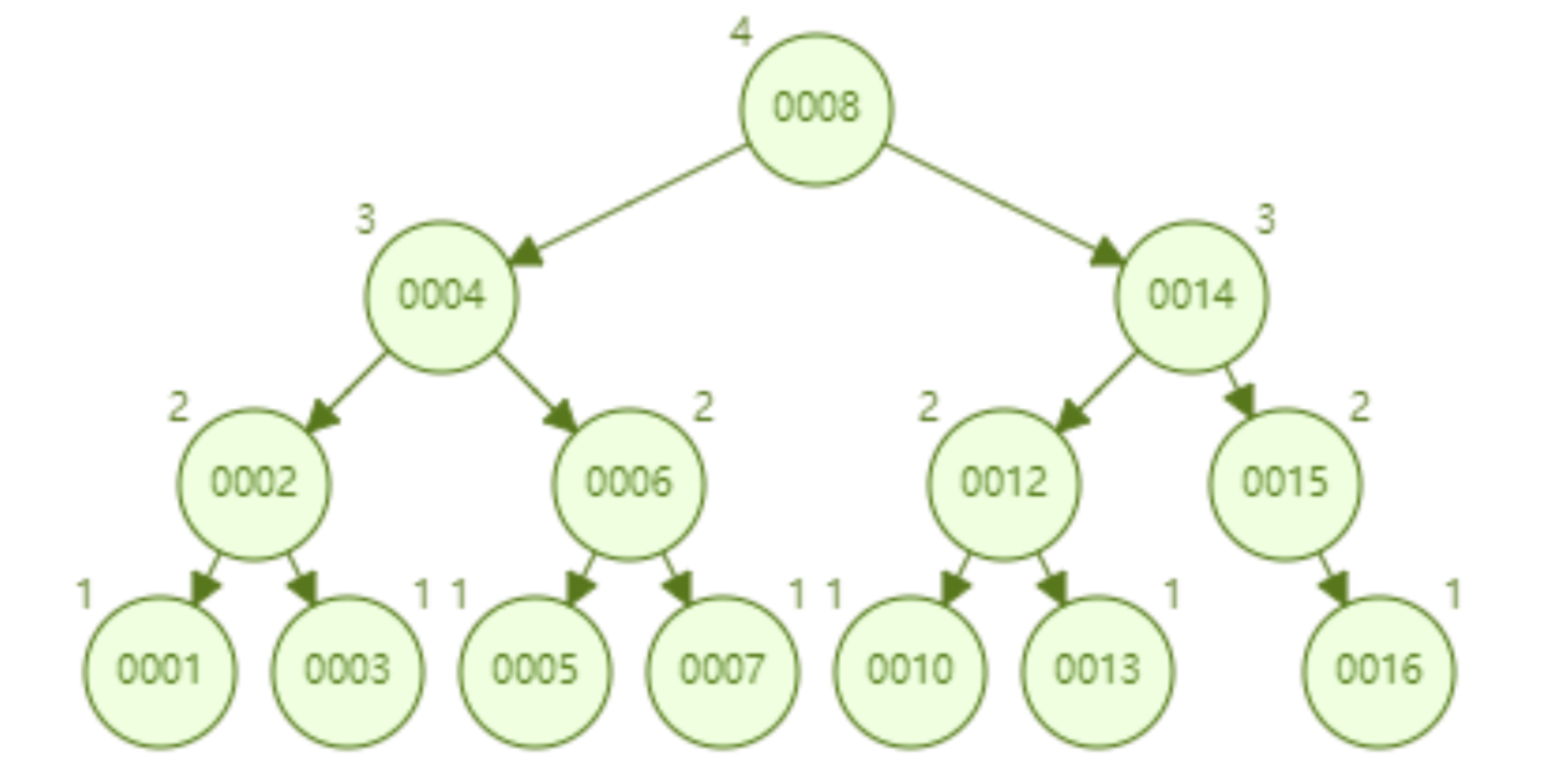
Summarize the advantages of AVL trees:

1. Good search performance (O(logn)), there is no extreme inefficient search situation.
   
2. Can realize range search and data sorting.
   

It seems that the AVL tree is really good as a data structure for data search, but the AVL tree is not suitable for the index data structure of the Mysql database, because consider this problem:

The bottleneck of database query data is disk IO. If we use AVL tree, each tree node only stores one data. We can only take out the data on one node and load it into the memory with one disk IO. For example, query id =7 We have to perform disk IO three times for this data, which is time consuming. Therefore, when designing database indexes, we need to first consider how to reduce the number of disk IOs as much as possible.

Disk IO has a characteristic that the time it takes to read 1B data and 1KB data from the disk is basically the same. Based on this idea, we can read as many times as possible on a tree node. Store data locally, and load more data into memory with one disk IO. This is the design principle of B-tree and B-tree.

B tree

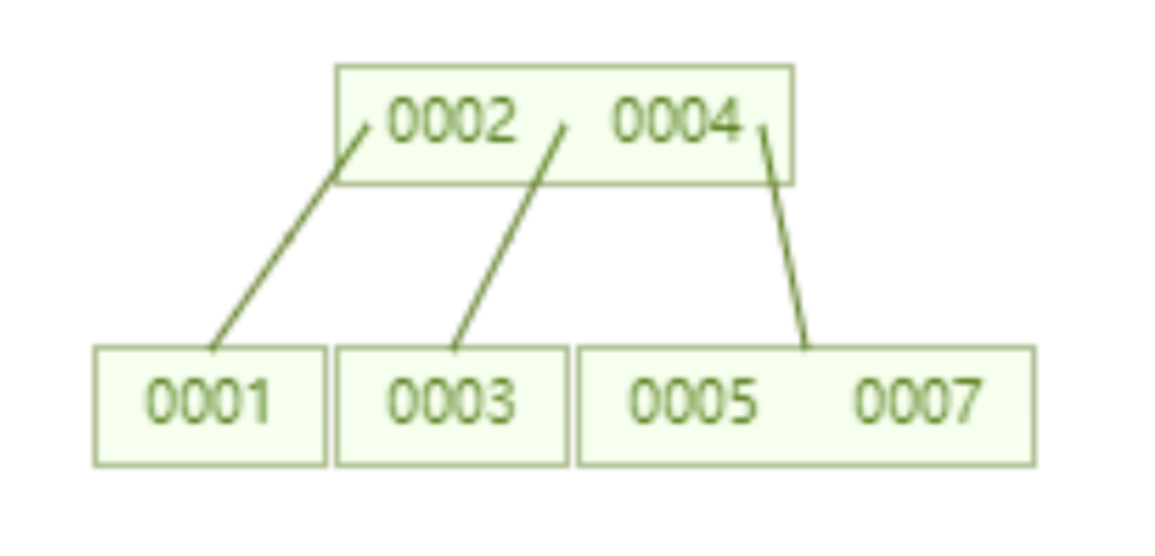
The following B tree is limited to storing up to two keys per node. If a node exceeds two The key will be automatically split. For example, the following B-tree stores 7 data. You only need to query two nodes to know the specific location of the data with id=7. That is, you can query the specified data with two disk IOs, which is better than the AVL tree.

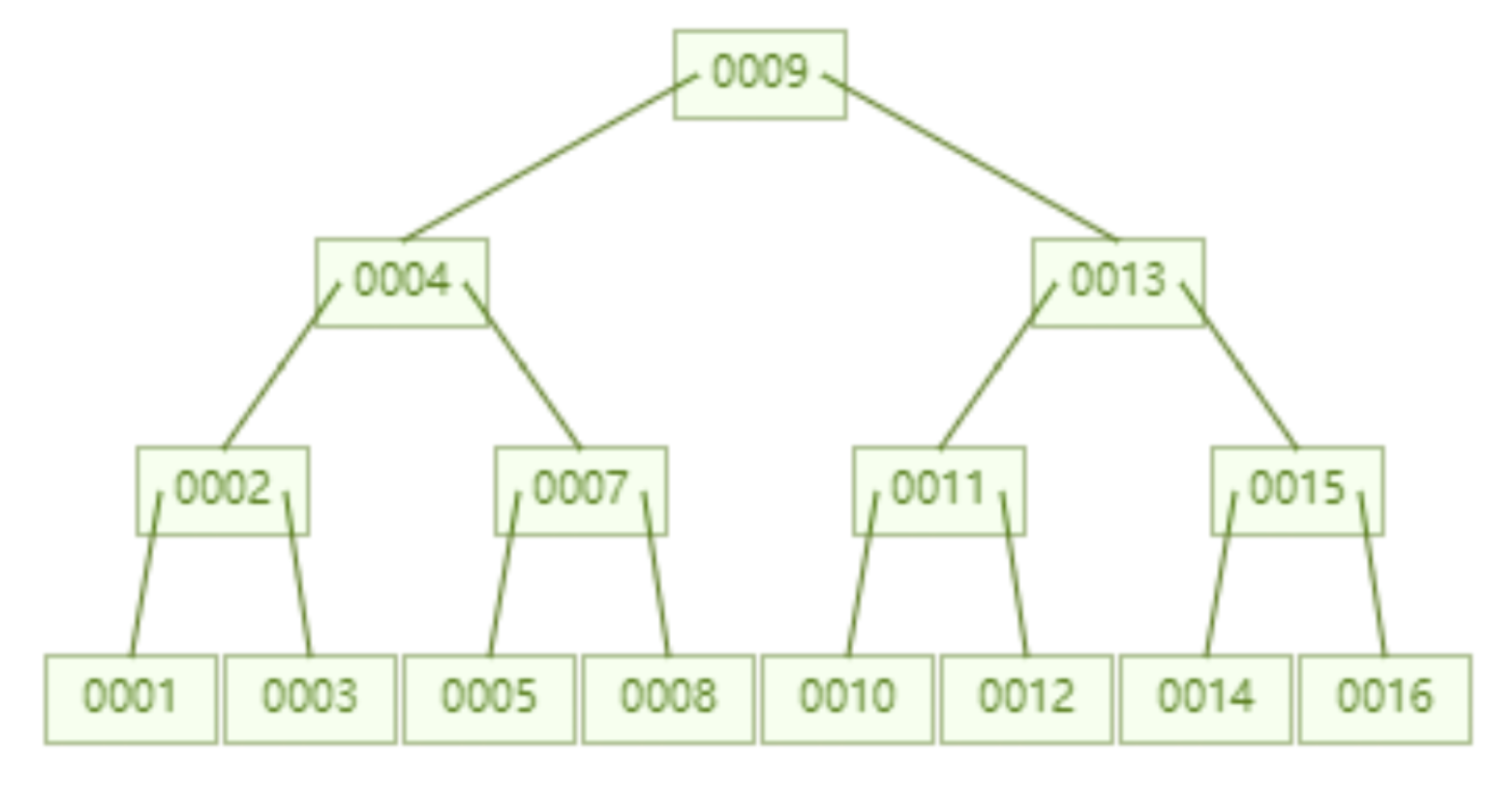
The following is a B-tree that stores 16 pieces of data. Similarly, each node stores up to 2 keys. Query The data with id=16 needs to be queried and compared on 4 nodes, which means 4 times of disk IO. Looks like query performance is the same as AVL tree.

But considering that the time consumed by disk IO to read one piece of data is basically the same as that of reading 100 pieces of data, then our optimization The idea can be changed to: read as much data as possible into the memory in one disk IO. This is directly reflected in the structure of the tree, that is, the key that each node can store can be increased appropriately.

When we set the key number limit for a single node to 6, a B-tree that stores 7 pieces of data will require 2 disk IOs to query the data with id=7.

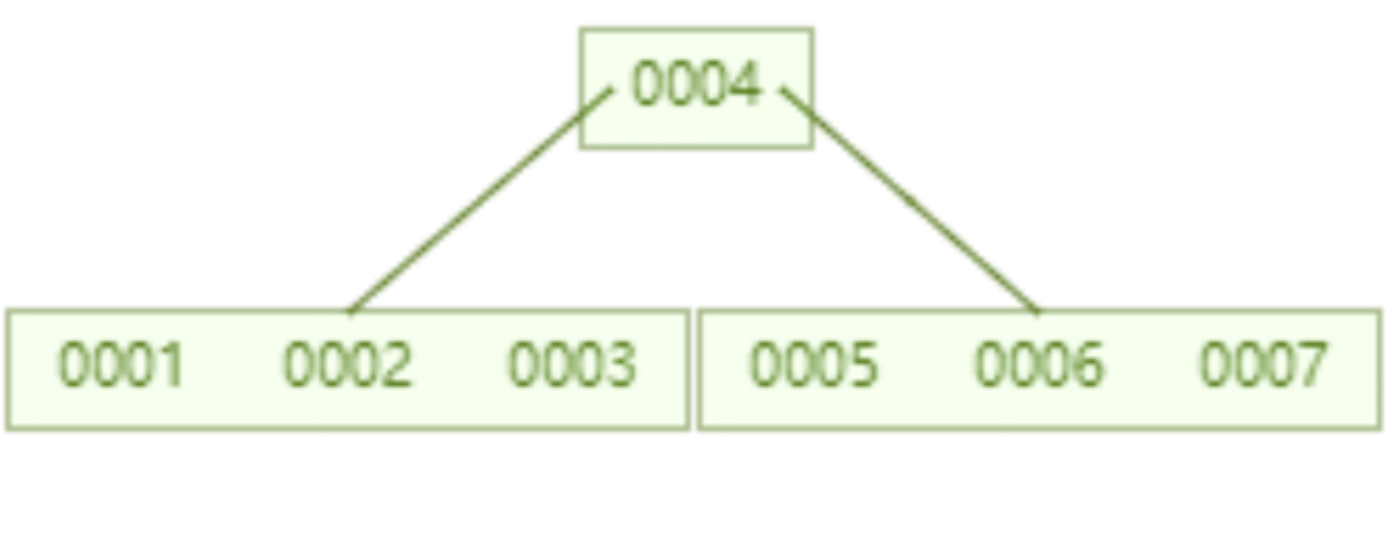
A B-tree that stores 16 pieces of data, querying the data with id=7 requires 2 disk IOs Second-rate. Compared with the AVL tree, the number of disk IOs is reduced to half.

So in terms of selection of database index data structure, B-tree is a very good choice. In summary, the B-tree used as a database index has the following advantages:

1. #Excellent retrieval speed, time complexity: The search performance of the B-tree is equal to O(h*logn), Among them, h is the height of the tree, n is the number of keywords in each node;
   
2. requires as little disk IO as possible to speed up the retrieval;
   
3. can support range Find.
   
4. B tree
   

What is the difference between B tree and B tree?

First, B tree stores data in one node, and B tree stores indexes (addresses), so one node in B tree cannot store a lot of data , but one node of the B-tree can store many indexes, and the leaf nodes of the B-tree store all the data.

Second, The leaf nodes of the B tree are connected in series using a linked list in the data stage to facilitate range search.

##Through the comparison between B-tree and B-tree, we can see that the B-tree node stores the index, and in a single node Even when storage capacity is limited, a single node can store a large number of indexes, reducing the height of the entire B-tree and reducing disk IO. Secondly, the leaf nodes of the B-tree are where the actual data is stored. The leaf nodes are connected using a linked list. The linked list itself is ordered and is more efficient when searching within the data range. Therefore, Mysql's index uses B-tree. B-tree has very good performance in search efficiency and range search.

2. Implementation of Innodb engine and Myisam engine

Mysql underlying data engine is designed in the form of plug-ins. The most common ones are Innodb engine and Myisam engine. Users can customize it according to their personal needs. It is necessary to choose a different engine as the underlying engine of the Mysql data table. We have just analyzed that B-tree is very suitable as the data structure of Mysql index, but how to organize the data and index also requires some design. The different design concepts also led to the emergence of Innodb and Myisam, each presenting unique performance.

MyISAM has excellent data lookup performance, but does not support transaction processing. The biggest feature of Innodb is that it supports ACID-compatible transaction functions, and it supports row-level locks. You can specify the engine when Mysql creates a table. For example, in the following example, Myisam and Innodb are specified as the data engines for the user table and user2 table respectively.

#After executing these two instructions, the system appears as follows The files indicate that the data and indexes of the two engines are organized differently.

The files generated by Innodb after creating the table are:

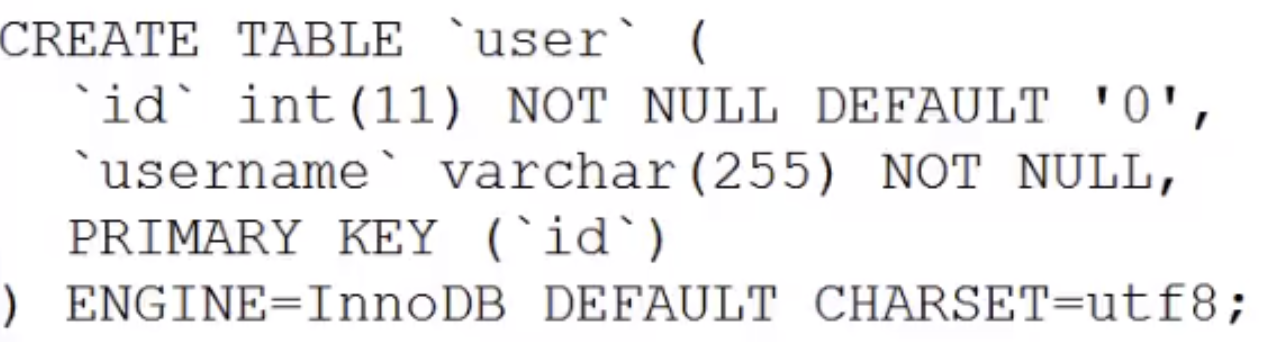
frm: Statement to create a table
• 
  
idb: Data index file in the table
• 
  

The files generated by Myisam after creating the table are

frm: Statement to create a table
• 
  
MYD: Data file in the table (myisam data)
• 
  
MYI: Index file in the table (myisam index)
• 
  

From the generated files, it appears that the underlying data and indexes of the two engines are organized in different ways. The MyISAM engine separates the data and indexes into one file for each person. This is called non-aggregation. Index mode; Innodb engine puts data and index in the same file, which is called clustered index mode. The following will analyze how these two engines rely on the B-tree data structure to organize engine implementation from the perspective of underlying implementation.

The underlying implementation of MyISAM engine (non-clustered index mode)

MyISAM uses a non-clustered index mode, that is, the data and index fall into two different on the file. When MyISAM creates a table, it uses the primary key as the KEY to create a primary index B-tree. The leaf nodes of the tree store the physical address of the corresponding data. After we get this physical address, we can directly locate the specific data record in the MyISAM data file.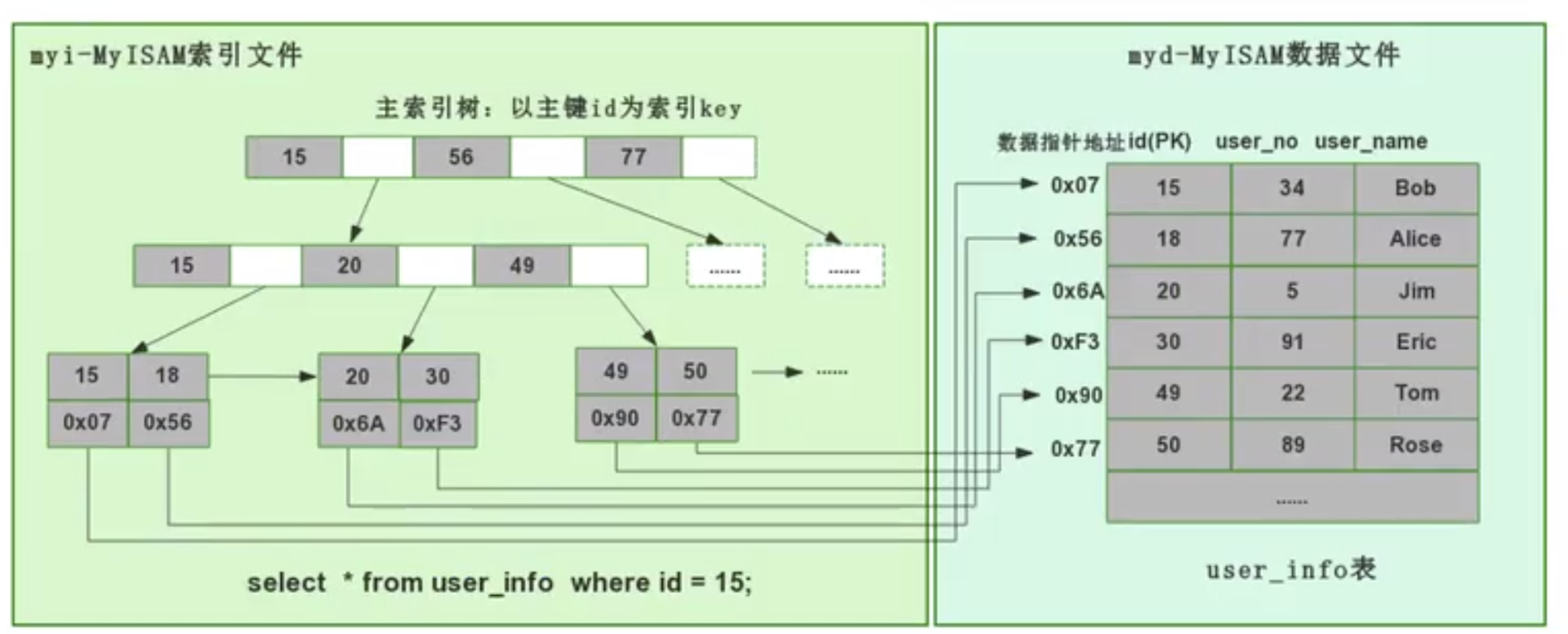

When we add an index to a field, we will also generate an index tree for the corresponding field. The leaf nodes of the index tree also record the physical address of the corresponding data, and then use this physical address to locate the specific data record in the data file.

The underlying implementation of the Innodb engine (clustered index method)

InnoDB is a clustered index method, so the data and index are stored in the same file. First, InnoDB will build an index B tree based on the primary key ID as KEY, as shown in the lower left figure. The leaf nodes of the B tree store the data corresponding to the primary key ID. For example, when executing the statement select * from user_info where id=15, InnoDB The primary key ID index B-tree will be queried to find the corresponding user_name='Bob'.

This is when InnoDB will automatically build the primary key ID index tree when creating a table. This is why Mysql requires the primary key to be specified when creating a table. How does InnoDB build an index tree when we add an index to a field in the table? For example, if we want to add an index to the user_name field, then InnoDB will create a user_name index B-tree. The KEY of user_name is stored in the node, and the data stored in the leaf nodes is the primary key KEY. Note that the leaves store the primary key KEY! After getting the primary key KEY, InnoDB will go to the primary key index tree to find the corresponding data based on the primary key KEY just found in the user_name index tree.

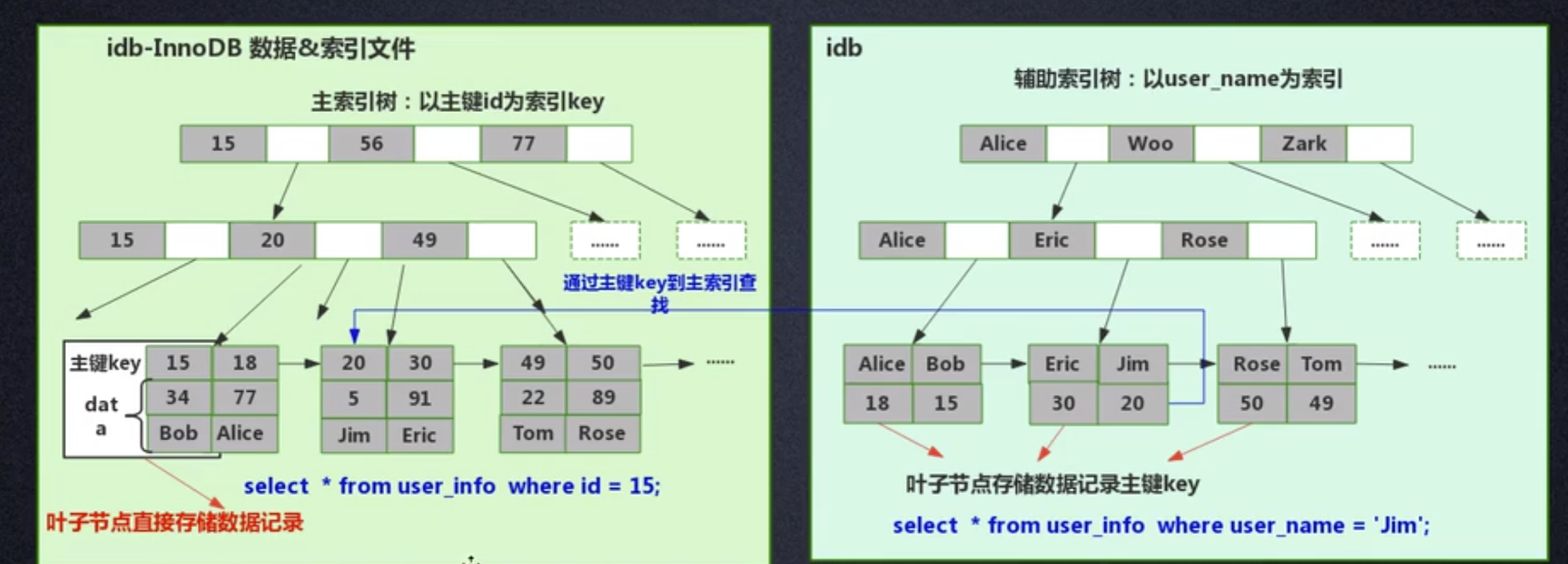
The question is, why does InnoDB only store specific data in the leaf nodes of the primary key index tree, but not in other index trees? What about the specific data? What if we need to find the primary key first and then find the corresponding data in the primary key index tree?

It's actually very simple, because InnoDB needs to save storage space. There may be many indexes in a table. InnoDB will generate an index tree for each indexed field. If the index tree of each field stores specific data, then the index data file of this table will become very huge (data Extremely redundant). From the perspective of saving disk space, there is really no need to store specific data in each field index tree. Through this seemingly "unnecessary" step, huge disk space is saved at the expense of less query performance. This It's very worthwhile.

When comparing the features of InnoDB and MyISAM, it was mentioned that MyISAM has better query performance. The reason can be seen from the design of the index file data file above: MyISAM can directly locate the physical address after directly finding it. Data records, but after InnoDB queries the leaf nodes, it needs to query the primary key index tree again to locate the specific data. It means that MyISAM can find the data in one step, but InnoDB requires two steps. Of course, MyISAM's query performance is higher.

This article first discusses which data structure is more suitable as the implementation of Mysql's underlying index, and then introduces the underlying implementation of Mysql's two classic data engines, MyISAM and InnoDB. Finally, let’s summarize when you need to add indexes to the fields in your table:

1. Fields that are frequently used as query conditions should be indexed;
   
2. Fields with poor uniqueness are not suitable for creating an index alone, even if the field is frequently used as a query condition;
   
3. Fields that are updated very frequently are not suitable for creating an index.
   

[Related recommendations: mysql video tutorial]

The above is the detailed content of Why is mysql index fast?. For more information, please follow other related articles on the PHP Chinese website!