A brief analysis of image distortion correction technology on the difficulties of smart car perception front-end processing

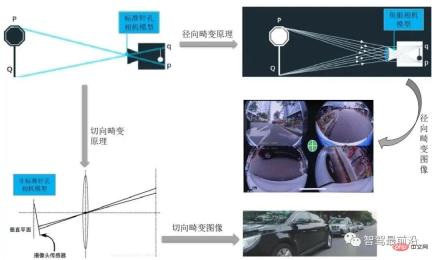
We know that when shooting images, the ideal position of the camera is perpendicular to the shooting plane, so as to ensure that the image can be reproduced according to the original geometric proportion. However, in the actual application of smart driving cars, due to the limitations of the smart car body structure, body control requires the camera to have a certain preview distance. The horizontal and vertical scanning surfaces of the camera usually expand in a fan shape, and the camera is generally in contact with the ground. Install at an angle. The existence of this angle will cause certain imaging distortion at the edge of the image. The result of distortion is a series of similar problems as follows during post-image processing:

1) Vertical lines are photographed as oblique lines, resulting in slope calculation errors;

2) Distant curves may be compressed due to distortion, resulting in curvature calculation errors, etc.;

3) For the side lane vehicle status, serious problems occur during the recognition process. Distortion will cause mismatching problems during post-processing;

Various problems such as the above may exist in the entire image perception. If the distortion is not handled properly, it will affect the entire image. Image quality and subsequent neural network recognition pose greater risks. In order to meet the real-time control requirements of smart cars, it is generally necessary to propose corresponding correction algorithms for camera image distortion in practical application scenarios.

01 The main types of distortion in smart cars

Camera distortion includes radial distortion, tangential distortion, centrifugal distortion, thin Prismatic distortion, etc. The camera distortions on smart cars mainly include radial distortion and tangential distortion.

Radial distortion is divided into barrel distortion and pincushion distortion.

Usually, the surround-view camera used in our smart parking system uses wide-angle shooting, and its corresponding distortion type is usually radial distortion. The main cause of radial distortion is the irregular change of the radial curvature of the lens, which will cause the distortion of the image. The characteristic of this distortion is that the principal point is the center and moves along the radial direction. The farther away it is, the farther away it is. The greater the amount of deformation produced. Severe radial distortion of a rectangle needs to be corrected into an ideal linear lens image before it can enter the back-end processing process.

The front-view, side-view, and rear-view cameras generally used in driving systems use general CMOS process cameras for shooting, and the lens may not be guaranteed during the installation process of the front-side view camera. Strictly parallel to the imaging plane, it may also be due to manufacturing defects that the lens is not parallel to the imaging plane, resulting in tangential distortion. This phenomenon usually occurs when the imager is attached to the camera.

There are a total of 5 distortion parameters in the radial distortion and tangential distortion models. In Opencv, they are arranged as A 5*1 matrix, containing k1, k2, p1, p2, k3 in sequence, is often defined in the form of a Mat matrix.

For distortion correction, these 5 parameters are the 5 distortion coefficients of the camera that need to be determined during camera calibration. The parameters k1, k2, and k3 are called radial distortion parameters, where k3 is an optional parameter. For cameras with severe distortion (such as eye cameras), there may also be k4, k5, and k6. Tangential distortion can be represented by two parameters p1 and p2: So far, a total of five parameters have been obtained: K1, K2, K3, P1, P2. These five parameters are necessary to eliminate distortion and are called distortion vectors, also They are called camera external parameters.

Therefore, after obtaining these five parameters, the deformation distortion of the image caused by lens distortion can be corrected. The following figure shows the effect after correction according to the lens distortion coefficient:

The formula to find the correct position of this point on the pixel plane through 5 distortion coefficients is as follows:

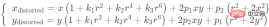
After distortion The point can be projected to the pixel plane through the internal parameter matrix to obtain the correct position (u, v) of the point on the image:

02 Image distortion correction method

Different from the camera model methodology, image dedistortion is to compensate for lens defects. Perform radial/tangential dedistortion and then use the camera model. The method of dealing with image distortion mainly involves which camera model to choose for image projection.

Typical camera model projection methods include spherical model and cylindrical model.

1. Fisheye camera imaging distortion correction

Usually similar to fisheye lens Produces great deformation. For example, during the imaging process of an ordinary camera, a straight line is still a straight line of a certain size when projected onto the image plane. However, when the image captured by a fisheye camera is projected onto the image plane, it will become a very large and long straight line, even in some scenes. Lower line detection is projected to infinity, so the pinhole model cannot model a fisheye lens.

In order to project the largest possible scene into a limited image plane, the first version of the fisheye lens is composed of more than a dozen different lenses. During the imaging process, the incident light After varying degrees of refraction and projection onto an imaging plane of limited size, the fisheye lens has a larger field of view compared with ordinary lenses.

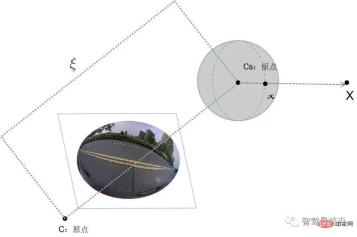
Research shows that the model followed by fisheye cameras when imaging is approximately the unit sphere projection model. Here, in order to better adapt to the derivation process of the camera pinhole model, the common method is to use the process of projection to the spherical camera model.

The analysis of the fisheye camera imaging process can be divided into two steps:

• Three-dimensional space points are linearly projected onto a sphere, Of course, this sphere is the virtual sphere we assume, and its center is considered to coincide with the origin of the camera coordinates.
• The point on the unit sphere is projected onto the image plane. This process is nonlinear.

The following figure shows the image processing process from a fisheye camera to a spherical camera in a smart driving system. Assume that the point in the camera coordinate system is X=(x,y,z) and the pixel coordinate is x=(u,v). Then its projection process is expressed as follows:

1) The first step is to use the camera to collect the three-dimensional image in the world coordinate system point, and project the imaging point in the image coordinate system onto the normalized unit spherical coordinates;

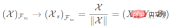
2) Deviating the camera coordinate center by units along the z-axis, we get the following:

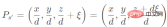
3) Consider the unit sphere and divide the spherical surface into Normalize to 1 unit:

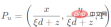
4) Transform the spherical projection model to the pinhole model to get The corresponding principal point coordinates, with which the corresponding standard camera coordinate system model can be established:

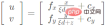
2. Cylindrical coordinate projection

For terminals such as front-view and side-view cameras, the images captured usually mainly produce tangential distortion. For tangential distortion, it is usually recommended to use a cylindrical camera model. Its advantage is that the user can switch the line of sight arbitrarily within a 360-degree range in a panoramic view such as a fisheye camera, and can also change the perspective on a line of sight to achieve the effect of getting closer or farther away. , at the same time, cylindrical panoramic images are also easier to process, because the cylindrical surface can be cut along the axis and unfolded on a plane. Traditional image processing methods can often be used directly. Cylindrical panoramic images do not require the camera to be calibrated very accurately. . Users have a 360-degree viewing angle in the horizontal direction and can also make certain changes in viewing angle in the vertical direction, but the angle range is limited. Since the image quality of the cylindrical model is uniform and the details are more realistic, it has a wider range of applications.

Generally speaking, the significant advantages of cylindrical panorama are summarized in the following two points:

1) The acquisition of its single photo The method is simpler than obtaining the cubic form and spherical form. Ordinary vehicle-mounted cameras (such as front-view and side-view cameras) can basically obtain original images.

2) The cylindrical panorama is easily expanded into a rectangular image, which can be directly stored and accessed using commonly used computer image formats. The cylindrical panorama allows the rotation angle of the participant's line of sight to be less than 180 degrees in the vertical direction, but in most applications, a 360-degree panoramic scene in the horizontal direction is sufficient to express spatial information.

Here we focus on the algorithm of how to use a cylindrical camera to correct distortion of the original image. In fact, this It is a process of obtaining the mapping relationship from the virtual camera to the original camera. The virtual camera here refers to the mapping relationship between real images and generated cylindrical images.

The following figure shows the image processing process of converting from ordinary vehicle camera shooting to cylindrical camera in a smart driving system. Among them, the essence of obtaining a virtual camera image is to find the mapping relationship between the virtual camera and the original camera. The general process is as follows:

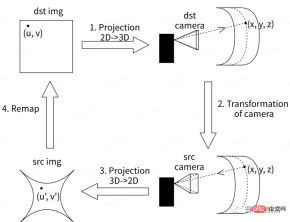
##First, the front/side view original video image can be set as the target image dst img; where the main point (u, v) on the target map is the basic point for 2D to 3D back projection transformation to the target camera coordinate map above, the target camera can reconstruct the point position (x, y, z) in the world coordinate system; then, the corresponding original camera image Src Camera under the virtual camera is obtained through the projection transformation algorithm in the three-dimensional coordinate system; after By performing a 3D to 2D projection transformation on the original camera image, the corresponding corrected image Src img (u', v') can be obtained. This image can be reconstructed to restore the original image dst img under the virtual camera.

It can be seen from the cylindrical camera model that the transformation formula from the cylindrical camera model to the pinhole camera model is as follows:

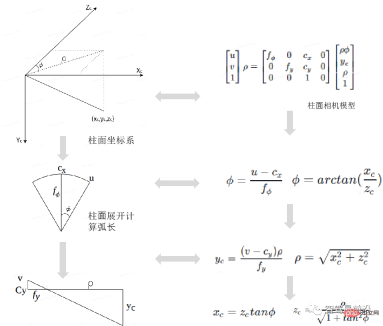
In the above formula, u and v represent the principal point of the pinhole camera plane (also called the coordinates in the pixel coordinate system), and fx, fy, cx, and cy represent manufacturing or installation errors. The two coordinate axis skew parameters generated. The principal point is multiplied by the radius distance in the cylindrical coordinate system to obtain the corresponding projection on the cylindrical coordinates.

ρ to perform polynomial approximation. The process of cylindrical camera 2D->3D space is uncertain. When Tdst=Tsrc, when ρ takes different values, from 3D space ->The mapping of the virtual camera obtained by the side-view/front-view camera 2D is the same; if Tdst! =Tsrc, the obtained virtual camera image changes with ρ. For a given cylindrical 2D position (u, v), under a given ρ condition, the 3D camera coordinates xc, yc, zc in the dst camera cylindrical coordinate system can be calculated according to the above formula.

Φ is used to perform polynomial approximation. Φ is the angle between the incident light and the image plane. This value is very similar to the parameters of a fisheye camera.

The next step is the camera transformation process, which can be summarized as follows.

First set the virtual camera image resolution to the resolution of the bird's-eye view IPM map you want to obtain; the principal point of the virtual camera image is the center of the IPM map resolution (generally assumed not to be set offset). Secondly, set the fx, fy and camera position of the virtual camera. The height is set to 1, which corresponds to the setting method of fx and fy. The offset of y can be modified according to needs. From this, the dst camera camera coordinates (xc, yc, zc) dst can be converted into the observation coordinate system vcs coordinates according to the external parameters (R, T) dst of the target camera dst camera, and then combined with the external parameters of the src camera ( R, T) src, convert VCS coordinates to src camera camera coordinates (xc, yc, zc) src.

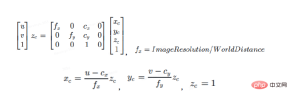
##03 Summary

Since car cameras usually carry different Imaging lens, this multi-element structure makes it impossible to simply adapt the original pinhole camera model to the analysis of the refraction relationship of the vehicle camera. Especially for fisheye cameras, due to the need to expand the viewing range, the image distortion caused by this refractive index is even more obvious. In this article, we focus on the de-distortion method adapted to various types of visual sensors in intelligent driving systems. We mainly use projection to project the image in the world coordinate system into the virtual spherical coordinate system and the virtual cylindrical coordinate system, thereby relying on 2D- >3D camera transformation to remove distortion. Some algorithms have been improved on the basis of long-term practice compared with the classic dedistortion algorithm.

The above is the detailed content of A brief analysis of image distortion correction technology on the difficulties of smart car perception front-end processing. For more information, please follow other related articles on the PHP Chinese website!