Scaling spherical deep learning to high-resolution input data
Translator | Zhu Xianzhong
Reviewer | Sun Shujuan
Traditional spherical CNN cannot be extended to high-resolution classification Task. In this paper, we introduce spherical scattering layers, a new type of spherical layer that can reduce the dimensionality of input data while retaining relevant information, and also has rotational equivariance properties.
Scattering networks work by using predefined convolution filters from wavelet analysis, rather than learning convolution filters from scratch. Since the scattering layer's weights are specifically designed rather than learned, the scattering layer can be used as a one-time preprocessing step, thereby reducing the resolution of the input data. Our previous experience shows that spherical CNNs equipped with an initial scattering layer can scale to resolutions of tens of millions of pixels, a feat that was previously unachievable with traditional spherical CNN layers.
Traditional spherical deep learning methods require calculation
Spherical CNN (document 1, 2, 3) is very useful for solving many different types of problems in machine learning , because many of these problems have data sources that cannot be naturally represented on a plane (for an introductory introduction to this, see our previous article at : https://towardsdatascience.com/geometric- deep-learning-for-spherical-data-55612742d05f).
A key feature of spherical CNNs is that they are equivariant to the rotation of spherical data (in this article, we focus on rotation equivariant methods). In practice, this means that spherical CNNs have impressive generalization properties, allowing them to do things like classify meshes of 3D objects regardless of how they are rotated (and whether they see the mesh during training different rotations).
We described## in recent published articles #KagenovaTeamA series of developments developed to improve the computational efficiency of spherical CNNAchievements(Reference address : https://towardsdatascience.com/efficient-generalized-spherical-cnns-1493426362ca). The method we adopted - efficient generalized spherical CNN - both retains the traditionThe equal variance characteristics of spherical CNN also make the calculation efficiency higher (Document 1). However, despite these advances in computational efficiency, spherical CNNs are still limited to relatively low-resolution data. This means that , Spherical CNNis currently not able to be applied to agitation that typically involves higher resolution data # in the application scenarios , such as cosmological data analysis and 360-degree computer vision of virtual reality and other fields. In a recently published article, we introduced the spherical scattering layer network to flexibly adjust the efficient general spherical CNN 来Improve the resolution (document 4), in this article we will review the content. Hybrid approach to support high-resolution input data
While developing an efficient universal spherical CNN (Reference 1), we discovered a very effective way to construct a sphere A hybrid approach to CNN architecture. Hybrid Spherical CNN can use different styles of spherical CNN layers in the same network, allowing developers to get the benefits of different types of layers at different stages of processing.
 The above picture shows an example of a hybrid spherical CNN architecture (please note: these layers are not a single one, but some different styles of spherical CNN layers ).
The above picture shows an example of a hybrid spherical CNN architecture (please note: these layers are not a single one, but some different styles of spherical CNN layers ).
Scattering Networks on Spheres continues this hybrid approach and introduces a new spherical CNN layer that can be plugged into existing spherical architectures. In order to extend the efficient general spherical CNN to higher dimensions, this new layer needs to have the following characteristics:
- Scalability with computational support
- Blending information to low frequencies to allow subsequent layers to run at lower resolutions
- Rotation Equivariance
- Provides stability and locally invariant representation (i.e., providing an efficient representation space)
# We determined that the scattering network layer has the potential to satisfy all of these characteristics enumerated above.
Scattering network on the sphere
The scattering network first proposed by Mallat (Reference 5) in the Euclidean environment can be regarded as having fixed convolution filtering For CNNs, these filters are derived from wavelet analysis. Scattering networks have proven to be very useful for traditional (Euclidean) computer vision, especially when data is limited - where learning convolutional filters is difficult. Next, we briefly discuss the inner workings of scattering network layers, how they meet the requirements defined in the previous section, and how they can be developed for spherical data analysis.
Data processing within the scattering layer is performed by three basic operations. The first building block is the fixed wavelet convolution, which is similar to the normal learning convolution used in Euclidean CNN. After wavelet convolution, the scattering network applies a modular nonlinear approach to the resulting representation. Finally, scattering utilizes a scaling function that performs a local averaging algorithm with some similarities to the pooling layers in ordinary CNNs. Repeated application of these three building blocks scatters the input data into a computational tree and extracts the resulting representation (similar to a CNN channel) from the tree at different stages of processing. A simplified schematic of these operations is shown below.

This figure illustrates the spherical scattering network of the spherical signal f. The signal is propagated via a cascaded spherical wavelet transform combined with an absolute value activation function represented by red nodes. The output of the scattering network is obtained by projecting these signals onto a spherical wavelet scaling function, resulting in the scattering coefficients represented by blue nodes.
From a traditional deep learning perspective, the operation of decentralized networks can seem a bit obscure. However, each computational operation described has a specific purpose - aiming to exploit the reliable theoretical results of wavelet analysis.
Wavelet convolutions in scattering networks are carefully derived to extract relevant information from the input data. For example, for natural images, wavelets are defined to specifically extract information related to edges at high frequencies and general shapes of objects at low frequencies. Therefore, in a planar setting, scatter network filters may have some similarities with traditional CNN filters. The same applies to the spherical setting, where we use scale-discretised wavelets (see Ref. 4 for details).
Since the wavelet filter is fixed, the initial scattering layer only needs to be applied once and does not need to be applied repeatedly throughout the training process (such as the initial layer in traditional CNN). This makes the scattering network computationally scalable, meeting the requirements of Feature 1 above. Furthermore, the scattering layer reduces the dimensionality of its input data, which means that only limited storage space needs to be used to cache the scattering representation when training downstream CNN layers.
Wavelet convolution is followed by a modular nonlinear method. First, this injects non-linear characteristics into the neural network layers. Secondly, the modulus operation mixes the high-frequency information in the input signal into the low-frequency data to meet the above requirement 2. The figure below shows the frequency distribution of the wavelet representation of the data before and after the modulus nonlinear calculation.

The above figure shows the distribution of wavelet coefficients at different spherical frequencies l before and after modular operation. Energy in the input signal moves from high frequencies (left panel) to low frequencies (right panel). where f is the input signal and Ψ represents the wavelet of scaling j.
After applying the modulus calculation, project the resulting signal onto the scaling function. The scaling function extracts low-frequency information from the representation results, similar to the pooling function operation in traditional CNN.
We empirically tested the theoretical equal variance properties of spherical scattering networks. The test is performed by rotating the signal and feeding it through the scattering network, and then comparing the resulting representation to the resulting representation of the input data after passing through the scattering network and then performing the rotation calculation. It can be demonstrated from the data in the table below that the equal variance error for a given depth is low, thus meeting the above requirement 3 (usually in practice, one path depth will not exceed the depth of two paths, because most of the signal energy has already been captured) .

Rotation equal variance error of spherical scattering network with different depths
Finally, it is theoretically proved Euclidean scattering networks are stable to small differentials or distortions(Documentation5). Currently, this result has been extended to the scattering network on the compact Riemannian manifold (document 6), especially the spherical surface Environment (Documentation4). In practice, stability to disparity morphology means that the representation computed by the scattering network will not differ significantly if the input is slightly changed (for a discussion of the role of stability in geometric deep learning, see our previous Post , address is https://towardsdatascience.com/a-brief-introduction-to-geometric-deep-learning-dae114923ddb). Thus, scattering networks provide a well-performing representation space on which subsequent learning can be efficiently performed, satisfying requirement 4 above.
Scalable and rotationally equivariant spherical CNN
Considering that the introduced scattering layer satisfies all our desired properties, next we are ready to integrate them into our of hybrid spherical CNN. As mentioned before, the scattering layer can be fixed onto the existing architecture as an initial pre-processing step to reduce the size of the representation for subsequent spherical layer processing.

In the image above, the scattering layer module (left of the dotted line) is a design layer. This means, it does not require training, while the remaining layers (right of the dotted line) are trainable. Therefore, this means that the scattering layer can be applied as a one-time preprocessing step to reduce the dimensionality of the input data.
Since scatter networks have a fixed representation of a given input, scatter network layers can be applied once to the entire dataset at the beginning of training and the resulting low-dimensional representation is cached to train subsequent layers . Fortunately, scatter representations have reduced dimensionality, which means that the disk space required to store them is relatively low. Due to the existence of this new spherical scattering layer, the efficient generalized spherical CNN can be extended to the domain of high-resolution classification problems.
Classification of cosmic microwave background anisotropy
How is matter distributed throughout the universe? This is a fundamental research question for cosmologists and has significant implications for theoretical models of the origin and evolution of our universe. The cosmic microwave background (CMB) - remnant energy from the Big Bang - maps the distribution of matter in the universe. Cosmologists observe the CMB on the celestial sphere, which requires computational methods that enable cosmological analysis within the celestial sphere.
Cosmologists are very interested in methods to analyze the cosmic microwave background because these methods can detect non-Gaussian properties in the distribution of the cosmic microwave background throughout space, which has important implications for theories of the early universe. of great significance. This analysis method also needs to be able to scale to astronomical resolution. We demonstrate that our scattering network meets these requirements by classifying CMB simulations as Gaussian or non-Gaussian with a resolution of L = 1024. The scattering network successfully classified these simulations with 95.3% accuracy, which is much better than the 53.1% achieved by the low-resolution traditional spherical CNN.

The above figure gives high-resolution simulation examples of Gaussian and non-Gaussian-like CMBs, which are used to evaluate the expansion of the spherical scattering network to high resolution. ability.
Summary
In this paper, we explored the ability of spherical scattering layers to compress the dimensionality of their input representations while still retaining important information for downstream tasks. We have shown that this makes scattering layers very useful for high-resolution sphere classification tasks. This opens the door to previously intractable potential applications such as cosmological data analysis and high-resolution 360 image/video classification. However, many computer vision problems such as segmentation or depth estimation that require dense predictions require both high-dimensional output and high-dimensional input. Finally, how to develop controllable spherical CNN layers that can increase the dimensionality of the output representation while maintaining equal variance is a current topic of research by Kagenova developers. These will be covered in the next article.
References
[1]Cobb, Wallis, Mavor-Parker, Marignier, Price, d'Avezac, McEwen, Efficient Generalized Spherical CNNs, ICLR (2021) , arXiv:2010.11661
[2] Cohen, Geiger, Koehler, Welling, Spherical CNNs, ICLR (2018), arXiv:1801.10130
[3] Esteves, Allen-Blanchette, Makadia, Daniilidis, Learning SO(3) Equivariant Representations with Spherical CNNs, ECCV (2018), arXiv:1711.06721
[4] McEwen, Jason , Wallis, Christopher and Mavor-Parker, Augustine N., Scattering Networks on the Sphere for Scalable and Rotationally Equivariant Spherical CNNs, ICLR (2022), arXiv:2102.02828
[5] Bruna , Joan, and Stéphane Mallat, Invariant scattering convolution networks, IEEE Transaction on Pattern Analysis and Machine Intelligence (2013)
[6] Perlmutter, Michael, et al., Geometric wavelet scattering networks on compact Riemannian manifolds, Mathematical and Scientific Machine Learning. PMLR (2020), arXiv:1905.10448
Translator introduction
Zhu Xianzhong, 51CTO community editor, 51CTO expert blog, Lecturer, computer teacher at a university in Weifang, and a veteran in the freelance programming industry.
Original title: Scaling Spherical Deep Learning to High-Resolution Input Data, Author: Jason McEwen, Augustine Mavor-Parker
The above is the detailed content of Scaling spherical deep learning to high-resolution input data. For more information, please follow other related articles on the PHP Chinese website!
 Personal Hacking Will Be A Pretty Fierce BearMay 11, 2025 am 11:09 AM
Personal Hacking Will Be A Pretty Fierce BearMay 11, 2025 am 11:09 AMCyberattacks are evolving. Gone are the days of generic phishing emails. The future of cybercrime is hyper-personalized, leveraging readily available online data and AI to craft highly targeted attacks. Imagine a scammer who knows your job, your f
 Pope Leo XIV Reveals How AI Influenced His Name ChoiceMay 11, 2025 am 11:07 AM
Pope Leo XIV Reveals How AI Influenced His Name ChoiceMay 11, 2025 am 11:07 AMIn his inaugural address to the College of Cardinals, Chicago-born Robert Francis Prevost, the newly elected Pope Leo XIV, discussed the influence of his namesake, Pope Leo XIII, whose papacy (1878-1903) coincided with the dawn of the automobile and
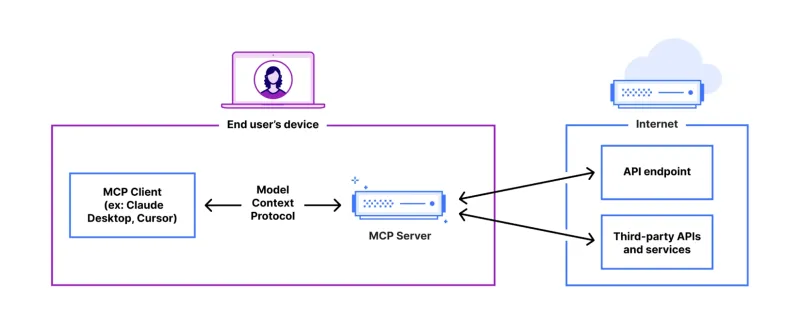 FastAPI-MCP Tutorial for Beginners and Experts - Analytics VidhyaMay 11, 2025 am 10:56 AM
FastAPI-MCP Tutorial for Beginners and Experts - Analytics VidhyaMay 11, 2025 am 10:56 AMThis tutorial demonstrates how to integrate your Large Language Model (LLM) with external tools using the Model Context Protocol (MCP) and FastAPI. We'll build a simple web application using FastAPI and convert it into an MCP server, enabling your L
 Dia-1.6B TTS : Best Text-to-Dialogue Generation Model - Analytics VidhyaMay 11, 2025 am 10:27 AM
Dia-1.6B TTS : Best Text-to-Dialogue Generation Model - Analytics VidhyaMay 11, 2025 am 10:27 AMExplore Dia-1.6B: A groundbreaking text-to-speech model developed by two undergraduates with zero funding! This 1.6 billion parameter model generates remarkably realistic speech, including nonverbal cues like laughter and sneezes. This article guide
 3 Ways AI Can Make Mentorship More Meaningful Than EverMay 10, 2025 am 11:17 AM
3 Ways AI Can Make Mentorship More Meaningful Than EverMay 10, 2025 am 11:17 AMI wholeheartedly agree. My success is inextricably linked to the guidance of my mentors. Their insights, particularly regarding business management, formed the bedrock of my beliefs and practices. This experience underscores my commitment to mentor
 AI Unearths New Potential In The Mining IndustryMay 10, 2025 am 11:16 AM
AI Unearths New Potential In The Mining IndustryMay 10, 2025 am 11:16 AMAI Enhanced Mining Equipment The mining operation environment is harsh and dangerous. Artificial intelligence systems help improve overall efficiency and security by removing humans from the most dangerous environments and enhancing human capabilities. Artificial intelligence is increasingly used to power autonomous trucks, drills and loaders used in mining operations. These AI-powered vehicles can operate accurately in hazardous environments, thereby increasing safety and productivity. Some companies have developed autonomous mining vehicles for large-scale mining operations. Equipment operating in challenging environments requires ongoing maintenance. However, maintenance can keep critical devices offline and consume resources. More precise maintenance means increased uptime for expensive and necessary equipment and significant cost savings. AI-driven
 Why AI Agents Will Trigger The Biggest Workplace Revolution In 25 YearsMay 10, 2025 am 11:15 AM
Why AI Agents Will Trigger The Biggest Workplace Revolution In 25 YearsMay 10, 2025 am 11:15 AMMarc Benioff, Salesforce CEO, predicts a monumental workplace revolution driven by AI agents, a transformation already underway within Salesforce and its client base. He envisions a shift from traditional markets to a vastly larger market focused on
 AI HR Is Going To Rock Our Worlds As AI Adoption SoarsMay 10, 2025 am 11:14 AM
AI HR Is Going To Rock Our Worlds As AI Adoption SoarsMay 10, 2025 am 11:14 AMThe Rise of AI in HR: Navigating a Workforce with Robot Colleagues The integration of AI into human resources (HR) is no longer a futuristic concept; it's rapidly becoming the new reality. This shift impacts both HR professionals and employees, dem


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.

Dreamweaver Mac version
Visual web development tools

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

SublimeText3 English version
Recommended: Win version, supports code prompts!

WebStorm Mac version
Useful JavaScript development tools







