CRPS: Scoring function for Bayesian machine learning models
Continuous Ranked Probability Score (CRPS) or "Continuous Ranked Probability Score" is a function or statistic that compares distribution predictions to true values.

#An important part of the machine learning workflow is model evaluation. The process itself can be considered common sense: split the data into training and test sets, train the model on the training set, and use a scoring function to evaluate its performance on the test set.
A scoring function (or metric) maps true values and their predictions to a single and comparable value [1]. For example, for continuous forecasting you can use scoring functions such as RMSE, MAE, MAPE, or R-squared. What if the forecast is not a point-by-point estimate, but a distribution?
In Bayesian machine learning, the prediction is usually not a point-by-point estimate, but a distribution of values. For example the predictions can be estimated parameters of a distribution, or in the non-parametric case, an array of samples from a MCMC method.
In this case, traditional scoring functions are not suitable for statistical designs; aggregation of predicted distributions into their mean or median values results in the loss of considerable information about the dispersion and shape of the predicted distributions.
CRPS
The Continuous Graded Probability Score (CRPS) is a fractional function that compares a single true value to a cumulative distribution function (CDF):
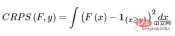
It was first introduced in the 1970s [4], mainly for weather forecasting, and is now receiving renewed attention in the literature and industry [1] [6]. It can be used as a metric to evaluate model performance when the target variable is continuous and the model predicts the distribution of the target; examples include Bayesian regression or Bayesian time series models [5].
CRPS is useful for both parametric and non-parametric predictions by using CDF: for many distributions, CRPS [3] has an analytical expression, and for non-parametric predictions, CRPS uses the empirical cumulative distribution function (eCDF) .
After calculating the CRPS for each observation in the test set, you also need to aggregate the results into a single value. Similar to RMSE and MAE, they are summarized using a (possibly weighted) mean:

The main challenge in comparing a single value to a distribution is how the individual value Convert to a representation of distribution. CRPS solves this problem by converting the ground truth into a degenerate distribution with an indicator function. For example, if the true value is 7, we can use:
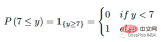
The indicator function is a valid CDF and can meet all the requirements of a CDF. The predicted distribution can then be compared with the degenerate distribution of the true values. We definitely want the predicted distribution to be as close to reality as possible; so this can be expressed mathematically by measuring the (squared) area between these two CDFs:

MAE to MAE relationship
CRPS is closely related to the famous MAE (Mean Absolute Error). If we use point-by-point prediction and treat it as a degenerate CDF and inject it into the CRPS equation, we can get:

So if the prediction distribution is a degenerate distribution (such as point-by-point estimation), then CRPS will be reduced to MAE. This helps us understand CRPS from another perspective: it can be seen as generalizing MAE to the prediction of distributions, or that MAE is a special case of CRPS when the prediction distribution degenerates.
When the prediction of the model is a parametric distribution (for example, distribution parameters need to be predicted), CRPS has an analytical expression for some common distributions [3]. If the model predicts the parameters μ and σ of the normal distribution, the CRPS can be calculated using the following formula:
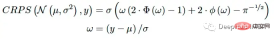
This solution can solve for known distributions such as Beta, Gamma, Logistic , lognormal distribution and others [3].
Computing the eCDF is a tedious task when the forecast is non-parametric, or more specifically - the forecast is a series of simulations. But CRPS can also be expressed as:

Where X, X' are F independent and identically distributed. These expressions are easier to compute, although they still require some computation.
Python implementation
import numpy as np # Adapted to numpy from pyro.ops.stats.crps_empirical # Copyright (c) 2017-2019 Uber Technologies, Inc. # SPDX-License-Identifier: Apache-2.0 def crps(y_true, y_pred, sample_weight=None): num_samples = y_pred.shape[0] absolute_error = np.mean(np.abs(y_pred - y_true), axis=0) if num_samples == 1: return np.average(absolute_error, weights=sample_weight) y_pred = np.sort(y_pred, axis=0) diff = y_pred[1:] - y_pred[:-1] weight = np.arange(1, num_samples) * np.arange(num_samples - 1, 0, -1) weight = np.expand_dims(weight, -1) per_obs_crps = absolute_error - np.sum(diff * weight, axis=0) / num_samples**2 return np.average(per_obs_crps, weights=sample_weight)
CRPS function implemented according to NRG form [2]. Adapted from pyroppl[6]
import numpy as np def crps(y_true, y_pred, sample_weight=None): num_samples = y_pred.shape[0] absolute_error = np.mean(np.abs(y_pred - y_true), axis=0) if num_samples == 1: return np.average(absolute_error, weights=sample_weight) y_pred = np.sort(y_pred, axis=0) b0 = y_pred.mean(axis=0) b1_values = y_pred * np.arange(num_samples).reshape((num_samples, 1)) b1 = b1_values.mean(axis=0) / num_samples per_obs_crps = absolute_error + b0 - 2 * b1 return np.average(per_obs_crps, weights=sample_weight)
The above code implements CRPS based on the PWM form[2].
Summary
Continuous Ranked Probability Score (CRPS) is a scoring function that compares a single true value to its predicted distribution. This property makes it relevant to Bayesian machine learning, where models typically output distribution predictions rather than point-wise estimates. It can be seen as a generalization of the well-known MAE for distribution prediction.
It has analytical expressions for parametric predictions and can perform simple calculations for non-parametric predictions. CRPS may become the new standard method for evaluating the performance of Bayesian machine learning models with continuous objectives.
The above is the detailed content of CRPS: Scoring function for Bayesian machine learning models. For more information, please follow other related articles on the PHP Chinese website!
 What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AM
What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AMIntroduction In prompt engineering, “Graph of Thought” refers to a novel approach that uses graph theory to structure and guide AI’s reasoning process. Unlike traditional methods, which often involve linear s
 Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AM
Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AMIntroduction Congratulations! You run a successful business. Through your web pages, social media campaigns, webinars, conferences, free resources, and other sources, you collect 5000 email IDs daily. The next obvious step is
 Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AM
Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AMIntroduction In today’s fast-paced software development environment, ensuring optimal application performance is crucial. Monitoring real-time metrics such as response times, error rates, and resource utilization can help main
 ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM
ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM“How many users do you have?” he prodded. “I think the last time we said was 500 million weekly actives, and it is growing very rapidly,” replied Altman. “You told me that it like doubled in just a few weeks,” Anderson continued. “I said that priv
 Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AM
Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AMIntroduction Mistral has released its very first multimodal model, namely the Pixtral-12B-2409. This model is built upon Mistral’s 12 Billion parameter, Nemo 12B. What sets this model apart? It can now take both images and tex
 Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AM
Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AMImagine having an AI-powered assistant that not only responds to your queries but also autonomously gathers information, executes tasks, and even handles multiple types of data—text, images, and code. Sounds futuristic? In this a
 Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AM
Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AMIntroduction The finance industry is the cornerstone of any country’s development, as it drives economic growth by facilitating efficient transactions and credit availability. The ease with which transactions occur and credit
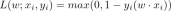 Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AM
Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AMIntroduction Data is being generated at an unprecedented rate from sources such as social media, financial transactions, and e-commerce platforms. Handling this continuous stream of information is a challenge, but it offers an


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Atom editor mac version download
The most popular open source editor

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

SublimeText3 Chinese version
Chinese version, very easy to use

WebStorm Mac version
Useful JavaScript development tools

VSCode Windows 64-bit Download
A free and powerful IDE editor launched by Microsoft






