 Technology peripherals
Technology peripherals AI
AI Working during the day and doing research at night, Google Brain research scientists solved a conjecture that has puzzled the mathematical community for decades.
Working during the day and doing research at night, Google Brain research scientists solved a conjecture that has puzzled the mathematical community for decades.In mid-October 2022, Justin Gilmer flew from California to New York to visit his former mentor Michael Saks, a mathematician at Rutgers University, on the East Coast.
During the reminiscing period, they did not talk about mathematics. In fact, Gilmer hasn’t thought seriously about math since earning his PhD at Rutgers University in 2015. At that time, he decided not to pursue a career in academia and began to teach himself programming. Over dinner with Saks, Gilmer told his mentor about his work at Google: machine learning and artificial intelligence.
While walking on the campus path, Gilmer recalled that in 2013, he spent more than a year walking on this path, thinking about a question called "the union closed set conjecture (also (called Frankl conjecture)" problem. This has always been a fruitless problem. For all his efforts, Gilmer only succeeded in teaching himself why this seemingly simple problem about a collection of numbers was so difficult to solve.
But after this visit seven years later, Gilmer suddenly had a new inspiration. He began to think about how to apply information theory to solve and close the set conjecture. After a month of research, the path to proof kept opening. In November, he published the results on arXiv, announcing significant progress in proving the entire conjecture.

##Paper link: https://arxiv.org/pdf/2211.09055.pdf
This paper set off a wave of subsequent research. Mathematicians at Oxford University, MIT, and the Institute for Advanced Study, among others, quickly began working on Gilmer's new method.
What is the union closed set conjecture?The closed set conjecture is related to sets of numbers, such as {1, 2} and {2, 3, 4}. You can perform operations on sets, including taking their union, which is merging them. For example, the union of {1, 2} and {2, 3, 4} is {1, 2, 3, 4}.
A set or family is said to be "union-closed" if the union of any two sets in the family is equal to any existing set in the family. For example, consider this family of four sets: {1}, {1, 2}, {2, 3, 4}, {1, 2, 3, 4}.
Combining any pair, you will get a set that already exists in the family, so this family is said to be a closed set.
Mathematicians have discussed and discussed the closed set conjecture as early as the 1960s, but it was not until 1979 that it received its first formal statement, in an article by Péter Frankl In the paper, he is a Hungarian mathematician who immigrated to Japan in the 1980s. In addition to mathematics, he also loves street performances.
Frankl conjectured that if a family of sets is a union of closed sets, then it must have at least one element (or number) that appears in at least half of the sets. This is a naturally occurring threshold for two reasons.

Justin Gilmer
First of all, In the example of a ready-made and closed family of sets, all elements appear in exactly 50% of the sets. For example, you could use the numbers 1 to 10 to form all the different sets, resulting in a total of 1024 such sets. They form a closed family of 512 sets in which each of the 10 elements appears.
When Frankl proposed this conjecture, no one had yet proposed an example of a closed set family in which the conjecture was not true. So 50% seems to be a correct prediction.
That doesn't mean it's easy to prove. Prior to Gilmer's work, many papers had only managed to establish thresholds that varied with the number of sets in the family (rather than a 50% threshold that was the same for all sizes of set families).
Will Sawin of Columbia University said: "It feels like it should be easy, and it is similar to a lot of easy problems, but it has never been conquered."
The lack of progress reflects both the intractable nature of the problem and the fact that many mathematicians would rather not think about it. They worry that they will waste years of their careers chasing an impossible problem. Gilmer remembers one day in 2013, when he went to Saks' office and mentioned this and the closed-set conjecture, and the instructors, who had also grappled with the problem, kicked him out of the room.
INSIGHTS OF UNCERTAINTY
After visiting Rutgers, Gilmer rolled the question through his mind, trying to understand why it was so difficult. He reminded himself of a basic fact: If you have a family of 100 set combinations, there are 4950 different ways to select two and combine them. Then he thought: How could 4950 different combinations map to 100 sets if no element appeared in these combinations at least with some frequency?
At this point, he was already on the road to resolution, even if he didn't know it yet.
Information theory was developed in the first half of the 20th century, most notably in Claude Shannon's 1948 paper "A Mathematical Theory of Communication." This paper provides a precise way to calculate the amount of information required to send a message, based on the amount of uncertainty surrounding what the message expresses. This connection between information and uncertainty is Shannon's remarkable insight.
Information theory appears frequently in combinatorics, a field of mathematics concerned with counting objects that Gilmer studied as a graduate student. But as he flew home to California, he worried that the way he related information theory to the union closed set conjecture was the naivety of an amateur.
"To be honest, I'm a little surprised that no one has thought of this before," Gilmer said. "But maybe I shouldn't be surprised, because I've been thinking about it for a year myself, and I know information theory."
Exploring the Problem
Gilmer's take on mathematics Studying comes from my love for mathematics. He is mainly busy with his daily work at Google on weekdays, and devotes himself to studying mathematical problems in his free time. He also carries a math textbook with him to work so he can look up forgotten formulas at any time. Gilmer keeps his feet on the ground but also looks to the stars—he likes reading the blogs of famed mathematician Tim Gowers, who keeps him inspired.
Gilmer said modestly: "Maybe you think people solving difficult mathematical problems shouldn't consult Chapter 2 of Elements of Information Theory, but I did."
The method proposed by Gilmer is to imagine a family of closed sets in which the probability of any element appearing in all sets is less than 1%. This is a counterexample that, if true, would falsify Frankl's conjecture.
Suppose two sets A and B are randomly selected from this family, ask: What is the probability that set A contains the number 1? What about set B? Since the probability of each element appearing in any given set is slightly less than 1%, you should not expect A or B to contain 1. This means that we wouldn't be surprised if neither actually contained 1, and certainly wouldn't gain much information.
Next, consider the probability that the union of A and B contains 1. This is still unlikely, but slightly greater than the probability of 1 appearing in either set alone, and is the sum of the probability of 1 appearing in A and the probability of 1 appearing in B minus the probability of 1 appearing in both . So the probability that the union of A and B contains 1 is about less than 2%.
This is still low, but closer to a 50% guess, which means more information is needed before the results can be shared. In other words, if there is a union-enclosing family of sets in which the probability of any element appearing in all sets is less than 1%, then the union of the two sets contains more information than either set by itself.
"The idea of proving the conjecture element by element is very clever," commented Ryan Alweiss of Princeton University.
Gilmer's work began to approach Frankl's suspicions. This is because it is easy to show that in a family of union-closed sets, the union of two sets must contain less information than the two sets themselves—not more.
The reason is simple. Take the union closed set family containing 1024 different sets as an example. The elements in each set are numbers from 1 to 10. If two of these sets are chosen at random, on average, a union of five elements will be obtained. (Of the 1024 sets, 252 contain five elements, which is the most common set size.) It's also possible that we'll get a union of about seven elements. But there are only 120 different combinations of ways to get a union of seven elements.
The point is that two randomly chosen sets contain elements with more uncertainty than their union. A union is more like a larger set with more elements and fewer possibilities. When you perform a union operation on two sets in a union-closed family of sets, you may know the result of the union, just like tossing a biased coin. You can easily guess which side the coin will land on. Union Contains less information than the two sets themselves.
Based on this, Gilmer believes that the probability of at least one element appearing in the set is greater than or equal to 1%. When Gilmer published his proof on November 16, he included a note - He believed that using his The method may be closer to the proof of the complete conjecture, potentially raising the threshold to 38%.
Five days later, three different groups of mathematicians published papers within hours of each other that built on Gilmer's work. The outbreak appears to have pushed Gilmer's approach to the extreme, though getting to 50 percent may require more new ideas.Still, some of the authors of the follow-up paper wondered why Gilmer didn't do the relatively simple 38% study himself. In fact, the reason is not complicated: after more than 5 years away from mathematics, Gilmer just didn't know how to do the technical analysis work to achieve this goal.
"I'm a little rusty, and honestly, I'm stuck," Gilmer said. “But I’m curious to see where the math community will take it.” But Gilmer also believes that the same reasons that cost him the opportunity to practice also, to some extent, cost him The proof first became possible: "This is the only explanation - why I thought about this problem for a year in graduate school and made no progress, and then returned to this problem after six years of leaving mathematics and made a breakthrough. In addition to machine learning, I don’t know any other explanation other than the change in my thinking.”
The above is the detailed content of Working during the day and doing research at night, Google Brain research scientists solved a conjecture that has puzzled the mathematical community for decades.. For more information, please follow other related articles on the PHP Chinese website!
 What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AM
What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AMIntroduction In prompt engineering, “Graph of Thought” refers to a novel approach that uses graph theory to structure and guide AI’s reasoning process. Unlike traditional methods, which often involve linear s
 Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AM
Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AMIntroduction Congratulations! You run a successful business. Through your web pages, social media campaigns, webinars, conferences, free resources, and other sources, you collect 5000 email IDs daily. The next obvious step is
 Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AM
Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AMIntroduction In today’s fast-paced software development environment, ensuring optimal application performance is crucial. Monitoring real-time metrics such as response times, error rates, and resource utilization can help main
 ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM
ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM“How many users do you have?” he prodded. “I think the last time we said was 500 million weekly actives, and it is growing very rapidly,” replied Altman. “You told me that it like doubled in just a few weeks,” Anderson continued. “I said that priv
 Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AM
Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AMIntroduction Mistral has released its very first multimodal model, namely the Pixtral-12B-2409. This model is built upon Mistral’s 12 Billion parameter, Nemo 12B. What sets this model apart? It can now take both images and tex
 Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AM
Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AMImagine having an AI-powered assistant that not only responds to your queries but also autonomously gathers information, executes tasks, and even handles multiple types of data—text, images, and code. Sounds futuristic? In this a
 Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AM
Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AMIntroduction The finance industry is the cornerstone of any country’s development, as it drives economic growth by facilitating efficient transactions and credit availability. The ease with which transactions occur and credit
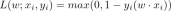 Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AM
Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AMIntroduction Data is being generated at an unprecedented rate from sources such as social media, financial transactions, and e-commerce platforms. Handling this continuous stream of information is a challenge, but it offers an


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

Zend Studio 13.0.1
Powerful PHP integrated development environment

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.

Dreamweaver CS6
Visual web development tools

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.





