 Technology peripherals
Technology peripherals AI
AI Physical Deep Learning with Biologically Inspired Training Methods: A Gradient-Free Approach to Physical Hardware
Physical Deep Learning with Biologically Inspired Training Methods: A Gradient-Free Approach to Physical HardwareThe growing demand for artificial intelligence has driven research into unconventional computing based on physical devices. While such computing devices mimic brain-inspired analog information processing, the learning process still relies on methods optimized for numerical processing, such as backpropagation, which are not suitable for physical implementation.
Here, a research team from Japan's NTT Device Technology Labs (NTT Device Technology Labs) and the University of Tokyoby extending a method called direct feedback alignment (DFA) Biologically inspired training algorithms to demonstrate physical deep learning. Unlike the original algorithm, the proposed method is based on random projections with alternative nonlinear activations. Therefore, physical neural networks can be trained without knowledge of the physical system and its gradients. Furthermore, the computation of this training can be simulated on scalable physical hardware.
The researchers demonstrated a proof-of-concept using an optoelectronic recurrent neural network called a deep reservoir computer. The potential for accelerated computing with competitive performance on benchmarks is demonstrated. The results provide practical solutions for training and acceleration of neuromorphic computing.
The research is titled "Physical deep learning with biologically inspired training method: gradient-free approach for physical hardware" and was released on December 26, 2022 In "Nature Communications".
Physical Deep Learning
The record-breaking performance of artificial neural network (ANN)-based machine learning in image processing, speech recognition, gaming, and more has successfully demonstrated its excellence Ability. Although these algorithms resemble the way the human brain works, they are essentially implemented at the software level using traditional von Neumann computing hardware. However, such digital computing-based artificial neural networks face problems in energy consumption and processing speed. These issues motivate the use of alternative physical platforms for the implementation of artificial neural networks.
Interestingly, even passive physical dynamics can be used as computational resources in randomly connected ANNs. Known as a Physical Reservoir Computer (RC) or Extreme Learning Machine (ELM), the ease of implementation of this framework greatly expands the choice of achievable materials and their range of applications. Such physically implemented neural networks (PNNs) are able to outsource task-specific computational load to physical systems.
Building deeper physical networks is a promising direction to further improve performance, as they can exponentially expand network expressive capabilities. This motivates proposals for deep PNNs using various physical platforms. Their training essentially relies on a method called backpropagation (BP), which has achieved great success in software-based ANNs. However, BP is not suitable for PNN in the following aspects. First, the physical implementation of BP operations remains complex and not scalable. Second, BP requires an accurate understanding of the entire physical system. Furthermore, when we apply BP to RC, these requirements undermine the unique properties of physical RC, namely that we need to accurately understand and simulate black-box physical stochastic networks.
Like BP in PNN, the difficulty of operating BP in biological neural networks has also been pointed out by the brain science community; the rationality of BP in the brain has always been questioned. These considerations have led to the development of biologically sound training algorithms.
A promising recent direction is direct feedback alignment (DFA). In this algorithm, a fixed random linear transformation of the final output layer error signal is used to replace the reverse error signal. Therefore, this method does not require layer-by-layer propagation of error signals or knowledge of weights. Furthermore, DFA is reported to be scalable to modern large network models. The success of this biologically motivated training suggests that there is a more suitable way to train PNN than BP. However, DFA still requires the derivative f'(a) of the nonlinear function f(x) for training, which hinders the application of the DFA method in physical systems. Therefore, larger scaling of DFA is important for PNN applications.
DFA and its enhancement for deep learning in physics
Here, researchers demonstrate deep learning in physics by enhancing the DFA algorithm. In the enhanced DFA, we replace the derivative of the physical nonlinear activation f'(a) in the standard DFA with an arbitrary nonlinear g(a) and show that the performance is robust to the choice of g(a). Due to this enhancement, it is no longer necessary to model f'(a) accurately. Since the proposed method is based on parallel stochastic projections with arbitrary nonlinear activations, the training computations can be performed on physical systems in the same way as physical ELM or RC concepts. This enables physical acceleration of inference and training.
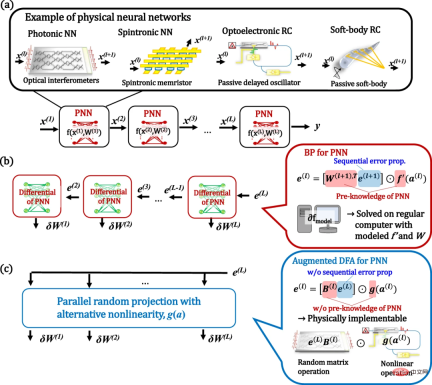
#Figure: Concept of PNN and its training through BP and augmented DFA. (Source: Paper)
#To demonstrate proof-of-concept, the researchers built an FPGA-assisted optoelectronic deep physics RC as a workbench. Although benchtop is simple to use and can be applied to a variety of physical platforms with only software-level updates, it achieves performance comparable to large and complex state-of-the-art systems.
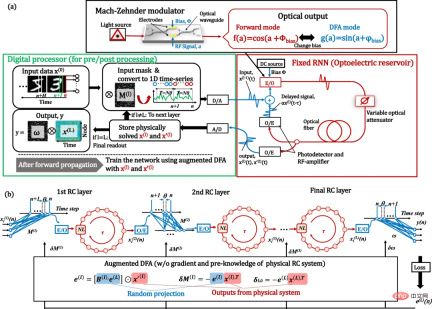
Figure: Optoelectronic depth RC system with enhanced DFA training. (Source: paper)
# In addition, the entire processing time, including the time of digital processing, was compared, and the possibility of physical acceleration of the training process was found.
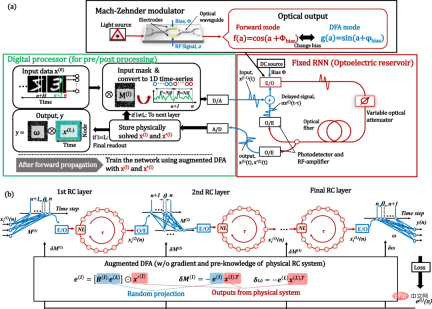
Figure: Performance of optoelectronic deep RC system. (Source: Paper)
The processing time budget for the RC bench breaks down as follows: FPGA processing (data transfer, memory allocation, and DAC/ADC) ~92%; 8% of digital processing is used for pre-/post-processing. Therefore, at the current stage, processing time is dominated by numerical calculations on FPGAs and CPUs. This is because the optoelectronic bench implements one reservoir using only one nonlinear delay line; these limitations could be relaxed by using fully parallel and all-optical computing hardware in the future. As can be seen, the computation on CPU and GPU shows a trend of O(N^2) for the number of nodes, while benchtop shows O(N), which is due to the data transfer bottleneck.
Physical acceleration outside the CPU is observed at N ~5,000 and ~12,000 for the BP and enhanced DFA algorithms, respectively. However, in terms of computational speed, effectiveness against GPUs has not been directly observed due to their memory limitations. By extrapolating the GPU trend, a physics speedup over the GPU can be observed at N ~80,000. To our knowledge, this is the first comparison of the entire training process and the first demonstration of physical training acceleration using PNNs.
To study the applicability of the proposed method to other systems, numerical simulations were performed using the widely studied photonic neural network. Furthermore, experimentally demonstrated delay-based RC is shown to be well suited for various physical systems. Regarding the scalability of physical systems, the main issue in building deep networks is their inherent noise. The effects of noise are studied through numerical simulations. The system was found to be robust to noise.
Scalability and limitations of the proposed approach
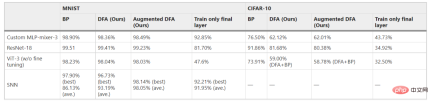
Here, the scalability of the DFA-based approach to more modern models is considered. One of the most commonly used models for practical deep learning is the deep connected convolutional neural network (CNN). However, it has been reported that the DFA algorithm is difficult to apply to standard CNNs. Therefore, the proposed method may be difficult to apply to convolutional PNNs in a simple manner.
Suitability for SNN is also an important topic considering the simulation hardware implementation. The applicability of DFA-based training to SNN has been reported, which means that the enhanced DFA proposed in this study can make training easier.
While DFA-based algorithms have the potential to be extended to more practical models than simple MLP or RC, the effectiveness of applying DFA-based training to such networks remains unknown. Here, as an additional work to this study, the scalability of DFA-based training (DFA itself and enhanced DFA) to the above mentioned models (MLP-Mixer, Vision transformer (ViT), ResNet and SNN) is investigated. DFA-based training was found to be effective even for exploratory practical models. Although the achievable accuracy of DFA-based training is essentially lower than that of BP training, some adjustments to the model and/or algorithm can improve performance. Notably, the accuracy of DFA and enhanced DFA was comparable for all experimental settings explored, suggesting that further improvements in DFA itself will directly contribute to improving enhanced DFA. The results show that the method can be extended to future implementations of practical models of PNNs, not just simple MLP or RC models.
Table 1: Applicability of enhanced DFA to real network models. (Source: paper)
BP and DFA in physical hardware
Generally Say, BP is very difficult to implement on physical hardware because it requires all the information in the computational graph. Therefore, training on physical hardware has always been done through computational simulations, which incurs large computational costs. Furthermore, differences between the model and the actual system lead to reduced accuracy. In contrast, enhanced DFA does not require accurate prior knowledge about the physical system. Therefore, in deep PNN, DFA-based methods are more effective than BP-based methods in terms of accuracy. Additionally, physical hardware can be used to accelerate computations.
In addition, DFA training does not require sequential error propagation calculated layer by layer, which means that the training of each layer can be performed in parallel. Therefore, a more optimized and parallel DFA implementation may lead to more significant speedups. These unique characteristics demonstrate the effectiveness of DFA-based methods, especially for neural networks based on physical hardware. On the other hand, the accuracy of the enhanced DFA-trained model is still inferior to that of the BP-trained model. Further improving the accuracy of DFA-based training remains future work.
Further physics speedup
The physics implementation demonstrates the speedup of RC loop processing with large-node numbers. However, its advantages are still limited and further improvements are needed. The processing time of the current prototype is expressed as data transfer and memory allocation to the FPGA. Therefore, integrating all processes into an FPGA will greatly improve performance at the expense of experimental flexibility. Furthermore, in the future, airborne optical methods will significantly reduce transmission costs. Large-scale optical integration and on-chip integration will further improve the performance of optical computing itself.
The above is the detailed content of Physical Deep Learning with Biologically Inspired Training Methods: A Gradient-Free Approach to Physical Hardware. For more information, please follow other related articles on the PHP Chinese website!
 GNN的基础、前沿和应用Apr 11, 2023 pm 11:40 PM
GNN的基础、前沿和应用Apr 11, 2023 pm 11:40 PM近年来,图神经网络(GNN)取得了快速、令人难以置信的进展。图神经网络又称为图深度学习、图表征学习(图表示学习)或几何深度学习,是机器学习特别是深度学习领域增长最快的研究课题。本次分享的题目为《GNN的基础、前沿和应用》,主要介绍由吴凌飞、崔鹏、裴健、赵亮几位学者牵头编撰的综合性书籍《图神经网络基础、前沿与应用》中的大致内容。一、图神经网络的介绍1、为什么要研究图?图是一种描述和建模复杂系统的通用语言。图本身并不复杂,它主要由边和结点构成。我们可以用结点表示任何我们想要建模的物体,可以用边表示两
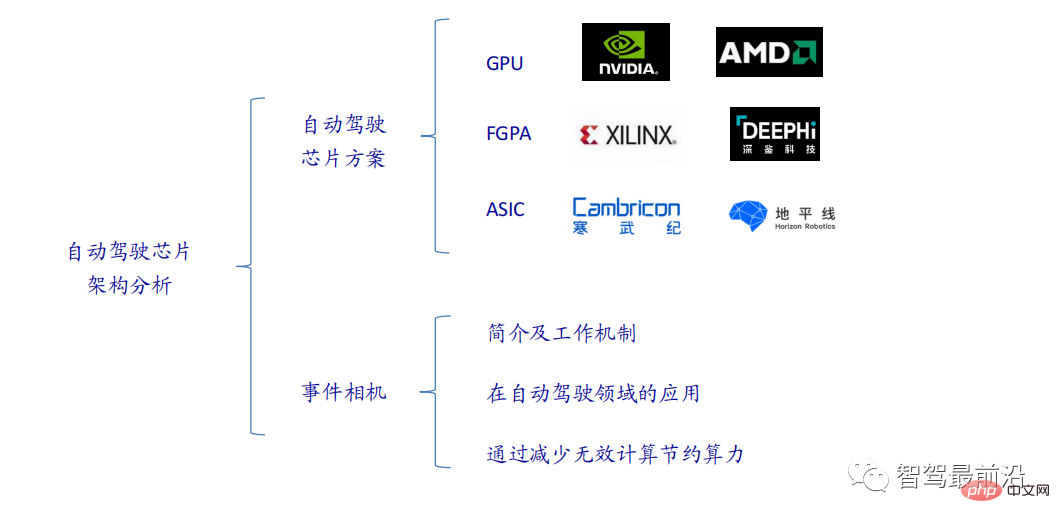 一文通览自动驾驶三大主流芯片架构Apr 12, 2023 pm 12:07 PM
一文通览自动驾驶三大主流芯片架构Apr 12, 2023 pm 12:07 PM当前主流的AI芯片主要分为三类,GPU、FPGA、ASIC。GPU、FPGA均是前期较为成熟的芯片架构,属于通用型芯片。ASIC属于为AI特定场景定制的芯片。行业内已经确认CPU不适用于AI计算,但是在AI应用领域也是必不可少。 GPU方案GPU与CPU的架构对比CPU遵循的是冯·诺依曼架构,其核心是存储程序/数据、串行顺序执行。因此CPU的架构中需要大量的空间去放置存储单元(Cache)和控制单元(Control),相比之下计算单元(ALU)只占据了很小的一部分,所以CPU在进行大规模并行计算
 "B站UP主成功打造全球首个基于红石的神经网络在社交媒体引起轰动,得到Yann LeCun的点赞赞赏"May 07, 2023 pm 10:58 PM
"B站UP主成功打造全球首个基于红石的神经网络在社交媒体引起轰动,得到Yann LeCun的点赞赞赏"May 07, 2023 pm 10:58 PM在我的世界(Minecraft)中,红石是一种非常重要的物品。它是游戏中的一种独特材料,开关、红石火把和红石块等能对导线或物体提供类似电流的能量。红石电路可以为你建造用于控制或激活其他机械的结构,其本身既可以被设计为用于响应玩家的手动激活,也可以反复输出信号或者响应非玩家引发的变化,如生物移动、物品掉落、植物生长、日夜更替等等。因此,在我的世界中,红石能够控制的机械类别极其多,小到简单机械如自动门、光开关和频闪电源,大到占地巨大的电梯、自动农场、小游戏平台甚至游戏内建的计算机。近日,B站UP主@
 扛住强风的无人机?加州理工用12分钟飞行数据教会无人机御风飞行Apr 09, 2023 pm 11:51 PM
扛住强风的无人机?加州理工用12分钟飞行数据教会无人机御风飞行Apr 09, 2023 pm 11:51 PM当风大到可以把伞吹坏的程度,无人机却稳稳当当,就像这样:御风飞行是空中飞行的一部分,从大的层面来讲,当飞行员驾驶飞机着陆时,风速可能会给他们带来挑战;从小的层面来讲,阵风也会影响无人机的飞行。目前来看,无人机要么在受控条件下飞行,无风;要么由人类使用遥控器操作。无人机被研究者控制在开阔的天空中编队飞行,但这些飞行通常是在理想的条件和环境下进行的。然而,要想让无人机自主执行必要但日常的任务,例如运送包裹,无人机必须能够实时适应风况。为了让无人机在风中飞行时具有更好的机动性,来自加州理工学院的一组工
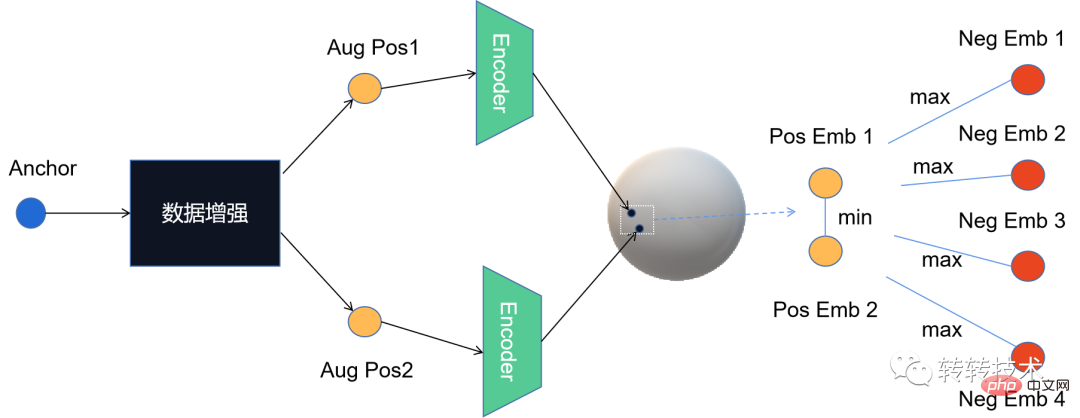 对比学习算法在转转的实践Apr 11, 2023 pm 09:25 PM
对比学习算法在转转的实践Apr 11, 2023 pm 09:25 PM1 什么是对比学习1.1 对比学习的定义1.2 对比学习的原理1.3 经典对比学习算法系列2 对比学习的应用3 对比学习在转转的实践3.1 CL在推荐召回的实践3.2 CL在转转的未来规划1 什么是对比学习1.1 对比学习的定义对比学习(Contrastive Learning, CL)是近年来 AI 领域的热门研究方向,吸引了众多研究学者的关注,其所属的自监督学习方式,更是在 ICLR 2020 被 Bengio 和 LeCun 等大佬点名称为 AI 的未来,后陆续登陆 NIPS, ACL,
 Michael Bronstein从代数拓扑学取经,提出了一种新的图神经网络计算结构!Apr 09, 2023 pm 10:11 PM
Michael Bronstein从代数拓扑学取经,提出了一种新的图神经网络计算结构!Apr 09, 2023 pm 10:11 PM本文由Cristian Bodnar 和Fabrizio Frasca 合著,以 C. Bodnar 、F. Frasca 等人发表于2021 ICML《Weisfeiler and Lehman Go Topological: 信息传递简单网络》和2021 NeurIPS 《Weisfeiler and Lehman Go Cellular: CW 网络》论文为参考。本文仅是通过微分几何学和代数拓扑学的视角讨论图神经网络系列的部分内容。从计算机网络到大型强子对撞机中的粒子相互作用,图可以用来模
 微软提出自动化神经网络训练剪枝框架OTO,一站式获得高性能轻量化模型Apr 04, 2023 pm 12:50 PM
微软提出自动化神经网络训练剪枝框架OTO,一站式获得高性能轻量化模型Apr 04, 2023 pm 12:50 PMOTO 是业内首个自动化、一站式、用户友好且通用的神经网络训练与结构压缩框架。 在人工智能时代,如何部署和维护神经网络是产品化的关键问题考虑到节省运算成本,同时尽可能小地损失模型性能,压缩神经网络成为了 DNN 产品化的关键之一。DNN 压缩通常来说有三种方式,剪枝,知识蒸馏和量化。剪枝旨在识别并去除冗余结构,给 DNN 瘦身的同时尽可能地保持模型性能,是最为通用且有效的压缩方法。三种方法通常来讲可以相辅相成,共同作用来达到最佳的压缩效果。然而现存的剪枝方法大都只针对特定模型,特定任务,且需要很
 用AI寻找大屠杀后失散的亲人!谷歌工程师研发人脸识别程序,可识别超70万张二战时期老照片Apr 08, 2023 pm 04:21 PM
用AI寻找大屠杀后失散的亲人!谷歌工程师研发人脸识别程序,可识别超70万张二战时期老照片Apr 08, 2023 pm 04:21 PMAI面部识别领域又开辟新业务了?这次,是鉴别二战时期老照片里的人脸图像。近日,来自谷歌的一名软件工程师Daniel Patt 研发了一项名为N2N(Numbers to Names)的 AI人脸识别技术,它可识别二战前欧洲和大屠杀时期的照片,并将他们与现代的人们联系起来。用AI寻找失散多年的亲人2016年,帕特在参观华沙波兰裔犹太人纪念馆时,萌生了一个想法。这一张张陌生的脸庞,会不会与自己存在血缘的联系?他的祖父母/外祖父母中有三位是来自波兰的大屠杀幸存者,他想帮助祖母找到被纳粹杀害的家人的照


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

SublimeText3 Linux new version
SublimeText3 Linux latest version

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

VSCode Windows 64-bit Download
A free and powerful IDE editor launched by Microsoft

Notepad++7.3.1
Easy-to-use and free code editor






