 Technology peripherals
Technology peripherals AI
AI Animation production efficiency increased by 80%! This AI software realizes high-precision video motion capture with one click
Animation production efficiency increased by 80%! This AI software realizes high-precision video motion capture with one clickAnimation production efficiency increased by 80%! This AI software realizes high-precision video motion capture with one click
AIGC has a new magic!
No need for animators' hand K, habit capture or light capture, just provide a video, this AI motion capture software can automatically output the action. In just a few minutes, the animation of the virtual human is completed.

Not only the large-frame movements of the limbs, but also the details of the hands can be accurately captured.
In addition to single-view video, it can also support multiple-view videos. Compared with other motion capture software that only supports monocular recognition, this software can provide higher motion capture quality.

At the same time, the software also supports editing and modification of recognized human body key points, smoothness, footstep details, etc. It can satisfy everything from the interest experience of ordinary players to the professional needs of hardcore players.
This is AIxPose, which has been developed by NetEase Interactive Entertainment AI Lab for many years, iteratively optimized and low-key based on professional art feedback. Video motion capture software. It is reported that the software has processed more than dozens of hours of video resources and has been used in the production process of game plot animations, popular dance animations and other resources. It has been verified by actual projects that a 1-minute dance animation may take more than 20 days to be produced by hand, but it only takes 3 days to produce with AIxPose assistance, and the entire process is shortened by more than 80%.
Recently, NetEase Interactive Entertainment AI Lab compiled the paper "Learning Analytical Posterior Probability" based on its experience in developing this software and related research work in the field of motion capture. for Human Mesh Recovery" was accepted by CVPR 2023, the top computer vision conference.

- Home page address: https://netease-gameai.github.io/ProPose/
- Paper address: https://netease-gameai.github.io/ProPose/static/assets/CVPR2023_ProPose.pdf
This paper innovatively proposes ProPose, a video motion capture technology based on posterior probability, which can achieve accurate three-dimensional human pose estimation under different settings such as single image and multi-sensor fusion. Technical accuracy is 19% higher than baseline probabilistic methods using priors, and outperforms past methods on the public datasets 3DPW, Human3.6M, and AGORA. In addition, for multi-sensor fusion tasks, this technology can also achieve higher accuracy than the baseline model without modifying the backbone of the neural network due to the introduction of new sensors.
Technical Background
The task of this research is to predict human mesh recovery (hmr) from RGB images. The existing methods can be summarized into two Category: direct method and indirect method. The direct method uses a neural network to regress the rotational representation of human joints end-to-end (such as axis angle, rotation matrix, 6D vector, etc.), while the indirect method first predicts some intermediate representations (such as three-dimensional key points, segmentation, etc.), and then passes these intermediate Indicates that the joint rotation is obtained.
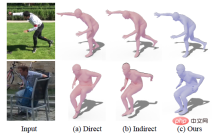
However, both types of methods have some problems. For direct methods, since this type of method requires the network to directly learn abstract representations such as rotation, compared with learning key points and segmentation, learning rotation is relatively difficult, so the results output by the network are sometimes difficult to align with the image and cannot be completed. Some large movements, such as the right foot in the first row in the picture below (a) cannot be fully extended back. In contrast, indirect methods generally produce higher accuracy, but the performance of such methods relies heavily on the accuracy of the intermediate representation. When the intermediate representation produces errors due to noise, it is easy for the final rotation to appear quite obvious. error, as shown in the left hand side of the second line in (b) below.
In addition to the aforementioned deterministic methods, there are also some methods to model the uncertainty of human posture by learning certain probability distributions, thereby Take noise into account to improve system robustness. Currently, the main probability modeling methods include multivariate Gaussian distribution, normalized flow, neural network implicit modeling, etc., but these probability distributions on non-SO (3) cannot truly reflect the uncertainty of joint rotation. For example, when the uncertainty is large, the local linearity assumption of the Gaussian distribution on SO (3) does not hold. A recent work directly uses the network to learn the parameters of the matrix Fisher distribution. Although this is a distribution on SO (3), the learning method of this method is similar to the direct method, and the convergence performance cannot be compared with the existing indirect method. .
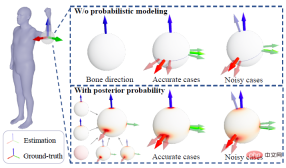
In order to take into account both high accuracy and robustness and improve the performance of probabilistic methods, ProPose derives the analytical posterior probability of joint rotation, which can not only benefit from the changes brought by different observation variables With high accuracy, it can also measure uncertainty and reduce the impact of noise on the algorithm as much as possible. As shown in the figure below, for the input image, ProPose can measure the uncertainty of the joint rotation in various directions to a certain extent through the output probability distribution, such as the rotation of the right hand along the arm axis, the direction of the left arm swinging up and down, and the left calf. The degree of distance, etc.
Technical implementation
Human body modeling
##This study conducts probability construction of human posture module, the goal is to find the posterior probability p (R|d,⋯) of joint rotation R under some observed variables (such as bone orientation d, etc.).
Specifically, since the joint rotation of the human body is located on SO (3), and the unit bone orientation of the child joint relative to the parent joint is located on S^2, it can be based on these two Analyze the probability distribution on a manifold.
First of all, the matrix Fisher distribution MF (⋅) on SO (3) can be used as the prior distribution of the joint rotation R, as shown in the following formula, F∈R^(3×3 ) are the parameters of the distribution, c (F) is a normalizing constant, and tr represents the trace of the matrix.
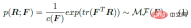
As shown in the following formula, F can be directly solved for the mean M and an aggregation term that represents the degree of distribution aggregation through SVD decomposition K. Among them, Δ=diag (1,1,|UV|) is a diagonal orthogonal matrix, which is used to ensure that the determinant of M is 1, so that it can fall in the special orthogonal group.
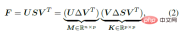
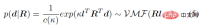
Using Bayesian theory, given the prior distribution p (R) and the likelihood function p (d|R), the posterior distribution of the joint rotation conditional on the bone orientation can be calculated. The analytical form of the posterior probability p (R|d):
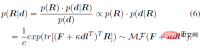
The above posterior probability only considers the orientation of the human skeleton as an observation quantity. Similarly, it can also be extended to other direction observation quantities d_i or rotation observation quantities D_j (which can be generated by other sensors) , such as IMUs, etc.), the analytical posterior probability is obtained in the following general form:
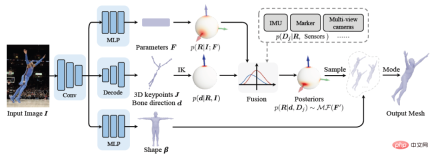
where κ_i and K_j are aggregation terms. g (⋅) is a mapping in the form of IK, which can convert direction observations into rotation estimates. It can adopt the simplest form such as g (d_i)=dl^T. Z_1 and Z_3 represent the set of direction observations and rotation observations respectively. Characteristics This section further explains that the posterior probability distribution has a higher probability than the prior probability distribution. degree of aggregation. The foregoing section introduces the analytical form of the posterior probability of human joint rotation, which is characterized by a new parameter F'. The posterior parameter F^' can be understood from another perspective, that is, F^' is the product of the mean term M that is the same as F and a new aggregation term K^': Where M^T dl^T=ll^T is a rank 1 real symmetric matrix, and K is also a real symmetric matrix, that is, the posterior aggregation term K' is also a real symmetric matrix. According to the staggered theorem about real symmetric matrices in matrix analysis, it can be obtained that the eigenvalues λ_i' of K' and the eigenvalues λ_i of K have the following inequality relationship: Considering that the eigenvalue of the aggregation term is equivalent to the singular value of the distribution parameter, and the singular value of the distribution parameter can reflect the confidence of the distribution, it can be concluded that when the likelihood term is non-zero, the posterior estimation ratio The prior estimate is more concentrated and can quickly converge to the mode preferred by the likelihood function, making it easier to learn. In addition to the prior probability method, another major benchmark method is to use inverse kinematics (IK) to directly calculate the rotation through the bone orientation. The following picture can intuitively show the posterior Comparison between probabilistic and deterministic IK methods. The above picture takes the human elbow joint as an example. The real three-dimensional coordinate axis represents the true value, and the transparent three-dimensional coordinate axis represents the estimated value. The first line represents the deterministic IK method. The modeling method behind this type of method is a vector representing the bone orientation. When the bone orientation is accurately estimated, the remaining one degree of freedom (twist) can be reduced to a circle (in the figure The dotted circle on the ball); when the bone orientation is estimated inaccurately, it will cause all possible estimates to deviate from the true value. The second line represents the posterior probability model of this study, which is a fusion of multiple different types of models. The red area on the sphere represents the probability of a certain rotation. Even if there is an error in the estimation of the bone orientation, this method may return it to the true state. value, because the noise of bone orientation can be mitigated as much as possible by a priori or other observations. Network framework diagram and loss function Based on the aforementioned theory and derivation, the following figure can be directly constructed frame diagram. A multi-branch network is used to estimate the prior distribution parameter F, the three-dimensional key point J (from which the bone orientation d is calculated), and the shape parameter β from a single image. The posterior probability is calculated through Bayes' rule, and finally the posture estimate can be obtained from the posterior distribution to output the human mesh. The selection of the loss function is relatively straightforward and is the weighted sum of the following four constraints, where L_J represents the key point constraint and L_β represents the shape parameter constraint. L_θ represents the attitude parameter constraint in matrix form, and L_s represents the attitude constraint after sampling the distribution. Regarding the constraints on the distribution, MAP is not used directly here because the numerical stability of the normalization parameters is considered. Regarding the sampling strategy, similar to the previous work, the matrix Fisher distribution is converted into the equivalent Bingham distribution in the quaternion form, and then obtained through rejection sampling, where the recommended distribution for rejection sampling adopts the angular central Gaussian distribution. In the experimental part, this study conducted a quantitative comparison with past methods on the public data sets Human3.6M, 3DPW, AGORA, and TotalCapture. It can be seen that the method of this study surpasses many previous methods. The last two gray rows in the table on the lower right are the work of the same period, and are listed here for the completeness of the list. 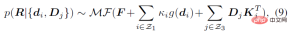
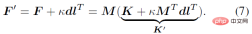
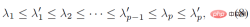
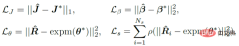
Experimental results
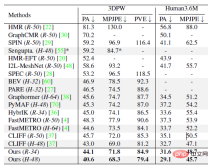
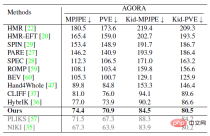
#The following figure shows the existing SOTA Qualitative comparison of methods HybrIK, PARE, and CLIFF shows that ProPose can achieve better results in some occlusion situations.

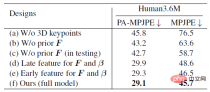
The following table shows a series of ablation experiments, mainly demonstrating the accuracy and robustness of ProPose. The benchmark methods include not using three-dimensional key points, not using priors, not using priors during testing, selecting features at different locations in the backbone network, etc. The table on the left below fully verifies that the proposed posterior probability distribution has higher accuracy. The table on the right below shows the comparison of the robustness to noise between the posterior method and the deterministic IK method. It can be seen that the posterior method can resist the interference of noise to a greater extent.

In addition to the above hmr tasks, this research also focuses on multi-sensor fusion tasks The evaluation was carried out on the above, and the effect of a single view and IMUs fusion is given below.
The above is the detailed content of Animation production efficiency increased by 80%! This AI software realizes high-precision video motion capture with one click. For more information, please follow other related articles on the PHP Chinese website!
 Most Used 10 Power BI Charts - Analytics VidhyaApr 16, 2025 pm 12:05 PM
Most Used 10 Power BI Charts - Analytics VidhyaApr 16, 2025 pm 12:05 PMHarnessing the Power of Data Visualization with Microsoft Power BI Charts In today's data-driven world, effectively communicating complex information to non-technical audiences is crucial. Data visualization bridges this gap, transforming raw data i
 Expert Systems in AIApr 16, 2025 pm 12:00 PM
Expert Systems in AIApr 16, 2025 pm 12:00 PMExpert Systems: A Deep Dive into AI's Decision-Making Power Imagine having access to expert advice on anything, from medical diagnoses to financial planning. That's the power of expert systems in artificial intelligence. These systems mimic the pro
 Three Of The Best Vibe Coders Break Down This AI Revolution In CodeApr 16, 2025 am 11:58 AM
Three Of The Best Vibe Coders Break Down This AI Revolution In CodeApr 16, 2025 am 11:58 AMFirst of all, it’s apparent that this is happening quickly. Various companies are talking about the proportions of their code that are currently written by AI, and these are increasing at a rapid clip. There’s a lot of job displacement already around
 Runway AI's Gen-4: How Can AI Montage Go Beyond AbsurdityApr 16, 2025 am 11:45 AM
Runway AI's Gen-4: How Can AI Montage Go Beyond AbsurdityApr 16, 2025 am 11:45 AMThe film industry, alongside all creative sectors, from digital marketing to social media, stands at a technological crossroad. As artificial intelligence begins to reshape every aspect of visual storytelling and change the landscape of entertainment
 How to Enroll for 5 Days ISRO AI Free Courses? - Analytics VidhyaApr 16, 2025 am 11:43 AM
How to Enroll for 5 Days ISRO AI Free Courses? - Analytics VidhyaApr 16, 2025 am 11:43 AMISRO's Free AI/ML Online Course: A Gateway to Geospatial Technology Innovation The Indian Space Research Organisation (ISRO), through its Indian Institute of Remote Sensing (IIRS), is offering a fantastic opportunity for students and professionals to
 Local Search Algorithms in AIApr 16, 2025 am 11:40 AM
Local Search Algorithms in AIApr 16, 2025 am 11:40 AMLocal Search Algorithms: A Comprehensive Guide Planning a large-scale event requires efficient workload distribution. When traditional approaches fail, local search algorithms offer a powerful solution. This article explores hill climbing and simul
 OpenAI Shifts Focus With GPT-4.1, Prioritizes Coding And Cost EfficiencyApr 16, 2025 am 11:37 AM
OpenAI Shifts Focus With GPT-4.1, Prioritizes Coding And Cost EfficiencyApr 16, 2025 am 11:37 AMThe release includes three distinct models, GPT-4.1, GPT-4.1 mini and GPT-4.1 nano, signaling a move toward task-specific optimizations within the large language model landscape. These models are not immediately replacing user-facing interfaces like
 The Prompt: ChatGPT Generates Fake PassportsApr 16, 2025 am 11:35 AM
The Prompt: ChatGPT Generates Fake PassportsApr 16, 2025 am 11:35 AMChip giant Nvidia said on Monday it will start manufacturing AI supercomputers— machines that can process copious amounts of data and run complex algorithms— entirely within the U.S. for the first time. The announcement comes after President Trump si


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Dreamweaver Mac version
Visual web development tools

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function

Atom editor mac version download
The most popular open source editor

VSCode Windows 64-bit Download
A free and powerful IDE editor launched by Microsoft

SublimeText3 Mac version
God-level code editing software (SublimeText3)





