 Technology peripherals
Technology peripherals AI
AI Overview of graph embedding: node, edge and graph embedding methods and Python implementation
Overview of graph embedding: node, edge and graph embedding methods and Python implementationGraph-based machine learning has made great progress in recent years. Graph-based methods have applications in many common problems in data science, such as link prediction, community discovery, node classification, etc. There are many ways to solve a problem depending on how you organize it and the data you have. This article will provide a high-level overview of graph-based embedding algorithms. Finally, we will also introduce how to use Python libraries (such as node2vec) to generate various embeddings on graphs.

Graph-based machine learning
Artificial intelligence has various branches, from recommendation systems, time series, natural Language processing, computer vision, graph machine learning, etc. There are several ways to solve common problems with graph-based machine learning. Including community discovery, link prediction, node classification, etc.
A major problem with machine learning on graphs is finding a way to represent (or encode) the structure of a graph so that machine learning models can easily exploit it [1]. Typically solving this problem in machine learning requires learning some kind of representation through structured tabular data associated with the model, which was previously done through statistical measurements or kernel functions. In recent years the trend has been towards encoding graphs to generate embedding vectors for training machine learning models.
The goal of machine learning models is to train machines to learn and recognize patterns at scale in data sets. This is amplified when working with graphs, as graphs provide different and complex structures that other forms of data (such as text, audio, or images) do not have. Graph-based machine learning can detect and explain recurring underlying patterns [2].
We may be interested in determining demographic information related to users on social networks. Demographic data includes age, gender, race, etc. Social media networks for companies like Facebook or Twitter range from millions to billions of users and trillions of sides. There will definitely be several patterns related to the demographics of the users in this network that are not easily detectable by humans or algorithms, but the model should be able to learn them. Similarly, we might want to recommend a pair of users to become friends, but they are not yet friends. This provides fodder for link prediction, another application of graph-based machine learning.
What is graph embedding?
Feature engineering refers to the common method of processing input data to form a set of features that provide a compact and meaningful representation of the original data set. The results of the feature engineering phase will serve as input to the machine learning model. This is a necessary process when working with tabular structured data sets, but is a difficult approach to perform when working with graph data, as a way needs to be found to generate a suitable representation associated with all graph data.
There are many ways to generate features representing structural information from graphs. The most common and straightforward method is to extract statistics from a graph. This can include recognition distribution, page rank, centrality metrics, jaccard score, etc. The required attributes are then incorporated into the model via a kernel function, but the problem with kernel functions is that the associated time complexity of generating the results is high.
Recent research trends have shifted towards finding meaningful graph representations and generating embedded representations for graphs. These embeddings learn graph representations that preserve the original structure of the network. We can think of it as a mapping function designed to transform a discrete graph into a continuous domain. Once a function is learned, it can be applied to a graph and the resulting mapping can be used as a feature set for machine learning algorithms.
Types of graph embedding
The analysis of graphs can be decomposed into 3 levels of granularity. Node level, edge level, and graph level (whole graph). Each level consists of a different process that generates embedding vectors, and the process chosen should depend on the problem and data being processed. Each of the granularity level embeddings presented below has accompanying figures to visually distinguish them from each other.
Node Embedding
At the node level, an embedding vector associated with each node in the graph is generated. This embedding vector can accommodate the representation and structure of the graph. Essentially nodes that are close to each other should also have vectors that are close to each other. This is one of the basic principles of popular node embedding models such as Node2Vec.
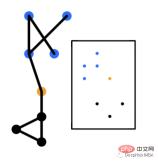
Edge Embedding
In the edge layer, an embedding vector is generated related to each edge in the graph. The link prediction problem is a common application using edge embedding. Link prediction refers to predicting the likelihood of whether an edge connects a pair of nodes. These embeddings can learn edge properties provided by the graph. For example, in a social network graph, you can have a multi-edge graph where nodes can be connected by edges based on age range, gender, etc. These edge properties can be learned by representing the correlation vector of the edge.

Graph embeddings
Graph-level embeddings are uncommon, they consist of generating an embedding vector representing each graph. For example, in a large graph with multiple subgraphs, each corresponding subgraph has an embedding vector that represents the graph structure. Classification problems are a common application where graph embeddings can be useful. These types of problems will involve classifying graphs into specific categories.

Python implementation
Using python code to implement the following libraries we need
Pythnotallow=3.9 networkx>=2.5 pandas>=1.2.4 numpy>=1.20.1 node2vec>=0.4.4 karateclub>=1.3.3 matplotlib>=3.3.4
If you do not have it installed node2vec package, please refer to its documentation. Install the karateclub package, which is also similar to
Node embedding
import random
import networkx as nx
import matplotlib.pyplot as plt
from node2vec import Node2Vec
from node2vec.edges import HadamardEmbedder
from karateclub import Graph2Vec
plt.style.use("seaborn")
# generate barbell network
G = nx.barbell_graph(
m1 = 13,
m2 = 7
)
# node embeddings
def run_n2v(G, dimensions=64, walk_length=80, num_walks=10, p=1, q=1, window=10):
"""
Given a graph G, this method will run the Node2Vec algorithm trained with the
appropriate parameters passed in.
Args:
G (Graph) : The network you want to run node2vec on
Returns:
This method will return a model
Example:
G = np.barbell_graph(m1=5, m2=3)
mdl = run_n2v(G)
"""
mdl = Node2Vec(
G,
dimensions=dimensions,
walk_length=walk_length,
num_walks=num_walks,
p=p,
q=q
)
mdl = mdl.fit(window=window)
return mdl
mdl = run_n2v(G)
# visualize node embeddings
x_coord = [mdl.wv.get_vector(str(x))[0] for x in G.nodes()]
y_coord = [mdl.wv.get_vector(str(x))[1] for x in G.nodes()]
plt.clf()
plt.scatter(x_coord, y_coord)
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.title("2 Dimensional Representation of Node2Vec Algorithm on Barbell Network")
plt.show()

The above picture is the visual node embedding generated by barbell graph, there are There are many methods for computing node embeddings, such as node2vec, deep walk, random walks, etc. node2vec is used here.
Edge Embedding
edges_embs = HadamardEmbedder(
keyed_vectors=mdl.wv
)
# visualize embeddings
coordinates = [
edges_embs[(str(x[0]), str(x[1]))] for x in G.edges()
]
plt.clf()
plt.scatter(coordinates[0], coordinates[1])
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.title("2 Dimensional Representation of Edge Embeddings on Barbell Network")
plt.show()
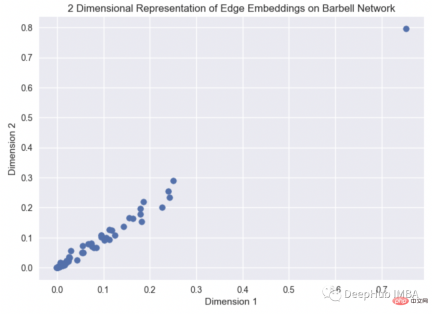
View the visualization of edge embedding through barbell graph, the source code of Hammard Embedder can be found here (https ://github.com/eliorc/node2vec/blob/master/node2vec/edges.py#L91).
Graph embedding
n_graphs = 10
Graphs = [
nx.fast_gnp_random_graph(
n = random.randint(5,15),
p = random.uniform(0,1)
) for x in range(n_graphs)
]
g_mdl = Graph2Vec(dimensions=2)
g_mdl.fit(Graphs)
g_emb = g_mdl.get_embedding()
x_coord = [vec[0] for vec in g_emb]
y_coord = [vec[1] for vec in g_emb]
plt.clf()
plt.scatter(x_coord, y_coord)
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.title("2 Dimensional Representation of Graph Embeddings on Randomly Generated Networks")
plt.show()
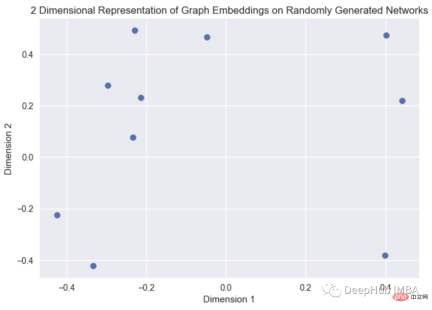
This is a graph embedding visualization of a randomly generated graph. The source code of the graph2vec algorithm can be found at Found here. (https://karateclub.readthedocs.io/en/latest/_modules/karateclub/graph_embedding/graph2vec.html)
Summary
Embedding is a function that maps discrete graphs to vector representations . Various forms of embeddings can be generated from graph data, node embeddings, edge embeddings and graph embeddings. All three types of embeddings provide a vector representation that maps the initial structure and features of the graph to numerical values in the X dimension.
The above is the detailed content of Overview of graph embedding: node, edge and graph embedding methods and Python implementation. For more information, please follow other related articles on the PHP Chinese website!
 解读CRISP-ML(Q):机器学习生命周期流程Apr 08, 2023 pm 01:21 PM
解读CRISP-ML(Q):机器学习生命周期流程Apr 08, 2023 pm 01:21 PM译者 | 布加迪审校 | 孙淑娟目前,没有用于构建和管理机器学习(ML)应用程序的标准实践。机器学习项目组织得不好,缺乏可重复性,而且从长远来看容易彻底失败。因此,我们需要一套流程来帮助自己在整个机器学习生命周期中保持质量、可持续性、稳健性和成本管理。图1. 机器学习开发生命周期流程使用质量保证方法开发机器学习应用程序的跨行业标准流程(CRISP-ML(Q))是CRISP-DM的升级版,以确保机器学习产品的质量。CRISP-ML(Q)有六个单独的阶段:1. 业务和数据理解2. 数据准备3. 模型
 2023年机器学习的十大概念和技术Apr 04, 2023 pm 12:30 PM
2023年机器学习的十大概念和技术Apr 04, 2023 pm 12:30 PM机器学习是一个不断发展的学科,一直在创造新的想法和技术。本文罗列了2023年机器学习的十大概念和技术。 本文罗列了2023年机器学习的十大概念和技术。2023年机器学习的十大概念和技术是一个教计算机从数据中学习的过程,无需明确的编程。机器学习是一个不断发展的学科,一直在创造新的想法和技术。为了保持领先,数据科学家应该关注其中一些网站,以跟上最新的发展。这将有助于了解机器学习中的技术如何在实践中使用,并为自己的业务或工作领域中的可能应用提供想法。2023年机器学习的十大概念和技术:1. 深度神经网
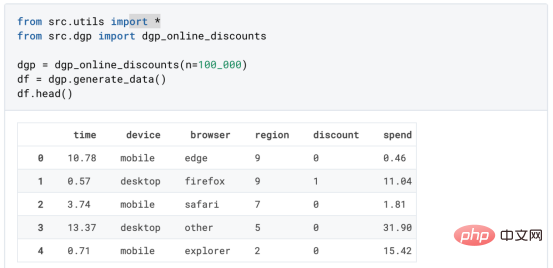 基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM
基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM译者 | 朱先忠审校 | 孙淑娟在我之前的博客中,我们已经了解了如何使用因果树来评估政策的异质处理效应。如果你还没有阅读过,我建议你在阅读本文前先读一遍,因为我们在本文中认为你已经了解了此文中的部分与本文相关的内容。为什么是异质处理效应(HTE:heterogenous treatment effects)呢?首先,对异质处理效应的估计允许我们根据它们的预期结果(疾病、公司收入、客户满意度等)选择提供处理(药物、广告、产品等)的用户(患者、用户、客户等)。换句话说,估计HTE有助于我
 使用PyTorch进行小样本学习的图像分类Apr 09, 2023 am 10:51 AM
使用PyTorch进行小样本学习的图像分类Apr 09, 2023 am 10:51 AM近年来,基于深度学习的模型在目标检测和图像识别等任务中表现出色。像ImageNet这样具有挑战性的图像分类数据集,包含1000种不同的对象分类,现在一些模型已经超过了人类水平上。但是这些模型依赖于监督训练流程,标记训练数据的可用性对它们有重大影响,并且模型能够检测到的类别也仅限于它们接受训练的类。由于在训练过程中没有足够的标记图像用于所有类,这些模型在现实环境中可能不太有用。并且我们希望的模型能够识别它在训练期间没有见到过的类,因为几乎不可能在所有潜在对象的图像上进行训练。我们将从几个样本中学习
 LazyPredict:为你选择最佳ML模型!Apr 06, 2023 pm 08:45 PM
LazyPredict:为你选择最佳ML模型!Apr 06, 2023 pm 08:45 PM本文讨论使用LazyPredict来创建简单的ML模型。LazyPredict创建机器学习模型的特点是不需要大量的代码,同时在不修改参数的情况下进行多模型拟合,从而在众多模型中选出性能最佳的一个。 摘要本文讨论使用LazyPredict来创建简单的ML模型。LazyPredict创建机器学习模型的特点是不需要大量的代码,同时在不修改参数的情况下进行多模型拟合,从而在众多模型中选出性能最佳的一个。本文包括的内容如下:简介LazyPredict模块的安装在分类模型中实施LazyPredict
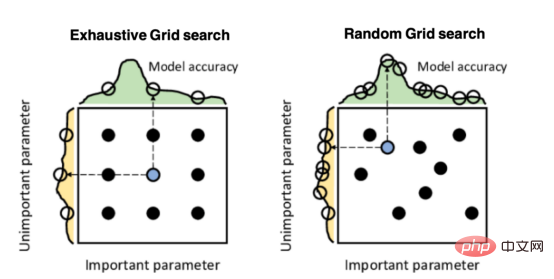 Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM
Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM译者 | 朱先忠审校 | 孙淑娟引言模型超参数(或模型设置)的优化可能是训练机器学习算法中最重要的一步,因为它可以找到最小化模型损失函数的最佳参数。这一步对于构建不易过拟合的泛化模型也是必不可少的。优化模型超参数的最著名技术是穷举网格搜索和随机网格搜索。在第一种方法中,搜索空间被定义为跨越每个模型超参数的域的网格。通过在网格的每个点上训练模型来获得最优超参数。尽管网格搜索非常容易实现,但它在计算上变得昂贵,尤其是当要优化的变量数量很大时。另一方面,随机网格搜索是一种更快的优化方法,可以提供更好的
 超参数优化比较之网格搜索、随机搜索和贝叶斯优化Apr 04, 2023 pm 12:05 PM
超参数优化比较之网格搜索、随机搜索和贝叶斯优化Apr 04, 2023 pm 12:05 PM本文将详细介绍用来提高机器学习效果的最常见的超参数优化方法。 译者 | 朱先忠审校 | 孙淑娟简介通常,在尝试改进机器学习模型时,人们首先想到的解决方案是添加更多的训练数据。额外的数据通常是有帮助(在某些情况下除外)的,但生成高质量的数据可能非常昂贵。通过使用现有数据获得最佳模型性能,超参数优化可以节省我们的时间和资源。顾名思义,超参数优化是为机器学习模型确定最佳超参数组合以满足优化函数(即,给定研究中的数据集,最大化模型的性能)的过程。换句话说,每个模型都会提供多个有关选项的调整“按钮
 人工智能自动获取知识和技能,实现自我完善的过程是什么Aug 24, 2022 am 11:57 AM
人工智能自动获取知识和技能,实现自我完善的过程是什么Aug 24, 2022 am 11:57 AM实现自我完善的过程是“机器学习”。机器学习是人工智能核心,是使计算机具有智能的根本途径;它使计算机能模拟人的学习行为,自动地通过学习来获取知识和技能,不断改善性能,实现自我完善。机器学习主要研究三方面问题:1、学习机理,人类获取知识、技能和抽象概念的天赋能力;2、学习方法,对生物学习机理进行简化的基础上,用计算的方法进行再现;3、学习系统,能够在一定程度上实现机器学习的系统。


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Dreamweaver CS6
Visual web development tools

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

WebStorm Mac version
Useful JavaScript development tools

Atom editor mac version download
The most popular open source editor

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.






