 Technology peripherals
Technology peripherals AI
AI AI can prove 82% of the problems in mathematical databases. The new SOTA has been achieved, and it is still based on Transformer.
AI can prove 82% of the problems in mathematical databases. The new SOTA has been achieved, and it is still based on Transformer.AI can prove 82% of the problems in mathematical databases. The new SOTA has been achieved, and it is still based on Transformer.

It has to be said that scientists have been obsessed with giving AI math lessons recently.
No, the Facebook team also joined in the fun and proposed a new model that can completely automate the demonstration of theorems and is significantly better than SOTA.
You must know that as mathematical theorems become more complex, it will only become more difficult to prove the theorems solely by human power.
Therefore, using computers to demonstrate mathematical theorems has become a research focus.
OpenAI has previously proposed a model GPT-f that specializes in this direction, which can demonstrate 56% of the problems in Metamath.
The latest method proposed this time can increase this number to 82.6%.
At the same time, researchers say that this method takes less time and can reduce computing consumption to one-tenth of the original compared to GPT-f.
Could it be said that this time AI will succeed in its battle with mathematics?
Or Transformer
The method proposed in this article is an online training program based on Transformer.
can be roughly divided into three steps:
First, pre-training in the mathematical proof library;
Second , Fine-tune the policy model on the supervised data set;
Third, Online training of the policy model and judgment model.
Specifically, it uses a search algorithm to let the model learn from the existing mathematical proof library, and then promotes and proves more problems.
The mathematical proof library includes three types, namely Metamath, Lean and a self-developed proof environment.
To put it simply, these proof libraries convert ordinary mathematical language into a form similar to a programming language.

Metamath’s main library is set.mm, which contains about 38,000 proofs based on ZFC set theory.
Lean is better known as Microsoft’s AI algorithm that can participate in IMO competitions. The Lean library is designed to teach the algorithm of the same name all the undergraduate mathematics knowledge and let it learn to prove these theorems.
The main goal of this research is to build a prover that can automatically generate a series of suitable strategies to prove the problem.
To this end, the researchers proposed a non-equilibrium hypergraph proof search algorithm based on MCTS.
MCTS is translated as Monte Carlo Tree Search, which is often used to solve game tree problems. It is well-known because of AlphaGo.
Its operation process is to find promising actions by randomly sampling in the search space, and then expand the search tree based on this action.
The idea adopted in this study is similar to this.
The search proof process starts from goal g, searches downward for methods, and gradually develops into a hypergraph.
When an empty set appears under a branch, it means that an optimal proof has been found.
Finally, during the backpropagation process, record the node values and total number of operations of the supertree.
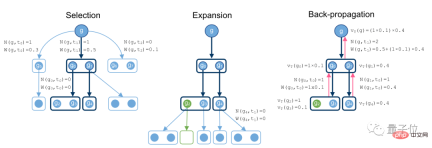
In this link, the researchers assumed a strategy model and a judgment model.
The strategy model allows sampling by judgment models, which can evaluate the current strategy's ability to find proof methods.
The entire search algorithm uses the above two models as a reference.
These two models are Transformer models and share weights.
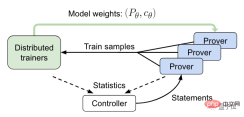
Next, comes the online training stage.
In this process, the controller will send the statement to asynchronous HTPS verification and collect training and proof data.
The validator will then send the training samples to the distributed trainer and periodically synchronize its model copies.
Experimental results
In the testing session, the researchers compared HTPS with GPT-f.
The latter is a mathematical theorem reasoning model previously proposed by OpenAI, also based on Transformer.
The results show that the model after online training can prove 82% of the problems in Metamath, far exceeding the previous record of 56.5% of GPT-f.

In the Lean library, this model can prove 43% of the theorems, which is 38% higher than SOTA. The following are the IMO test questions proved by this model.

#But it’s not perfect yet.
For example, in the following question, it did not solve the question in the simplest way. The researchers said this was because of errors in the annotations.

One More Thing
Using computers to demonstrate mathematical problems, the proof of the four-color theorem is one of the most well-known examples.
The four-color theorem is one of the three major problems in modern mathematics. It states that "any map can use only four colors to color countries with common borders in different colors."
Because the demonstration of this theorem requires a lot of calculations, no one could fully demonstrate it within 100 years after it was proposed.
Until 1976, after 1,200 hours and 10 billion judgments on two computers at the University of Illinois, it was finally possible to demonstrate that any map only needs 4 colors to mark it. It caused a sensation in the entire mathematical community.
In addition, as mathematical problems become more complex, it becomes more difficult to use human power to check whether the theorem is correct.
Recently, the AI community has gradually focused on mathematical problems.
In 2020, OpenAI launched the mathematical theorem reasoning model GPT-f, which can be used for automatic theorem proof.
This method can complete 56.5% of the proofs in the test set, exceeding the then SOTA model MetaGen-IL by more than 30%.
In the same year, Microsoft also released Lean, which can make IMO test questions, which means that AI can make questions that it has never seen before.
Last year, after OpenAI added a verifier to GPT-3, the effect of doing math problems was significantly better than the previous fine-tuning method, and it could reach 90% of the level of primary school students.
In January this year, a joint study from MIT, Harvard, Columbia University, and the University of Waterloo showed that the model they proposed can do high math.
In short, scientists are working hard to make AI, a partial subject, become both liberal arts and sciences.
The above is the detailed content of AI can prove 82% of the problems in mathematical databases. The new SOTA has been achieved, and it is still based on Transformer.. For more information, please follow other related articles on the PHP Chinese website!
 What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AM
What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AMIntroduction In prompt engineering, “Graph of Thought” refers to a novel approach that uses graph theory to structure and guide AI’s reasoning process. Unlike traditional methods, which often involve linear s
 Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AM
Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AMIntroduction Congratulations! You run a successful business. Through your web pages, social media campaigns, webinars, conferences, free resources, and other sources, you collect 5000 email IDs daily. The next obvious step is
 Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AM
Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AMIntroduction In today’s fast-paced software development environment, ensuring optimal application performance is crucial. Monitoring real-time metrics such as response times, error rates, and resource utilization can help main
 ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM
ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM“How many users do you have?” he prodded. “I think the last time we said was 500 million weekly actives, and it is growing very rapidly,” replied Altman. “You told me that it like doubled in just a few weeks,” Anderson continued. “I said that priv
 Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AM
Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AMIntroduction Mistral has released its very first multimodal model, namely the Pixtral-12B-2409. This model is built upon Mistral’s 12 Billion parameter, Nemo 12B. What sets this model apart? It can now take both images and tex
 Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AM
Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AMImagine having an AI-powered assistant that not only responds to your queries but also autonomously gathers information, executes tasks, and even handles multiple types of data—text, images, and code. Sounds futuristic? In this a
 Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AM
Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AMIntroduction The finance industry is the cornerstone of any country’s development, as it drives economic growth by facilitating efficient transactions and credit availability. The ease with which transactions occur and credit
 Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AM
Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AMIntroduction Data is being generated at an unprecedented rate from sources such as social media, financial transactions, and e-commerce platforms. Handling this continuous stream of information is a challenge, but it offers an


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

VSCode Windows 64-bit Download
A free and powerful IDE editor launched by Microsoft

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

WebStorm Mac version
Useful JavaScript development tools





