 Technology peripherals
Technology peripherals AI
AI The recently popular Diffusion Model, the first review of diffusion generation models!
The recently popular Diffusion Model, the first review of diffusion generation models!The recently popular Diffusion Model, the first review of diffusion generation models!

This review (Diffusion Models: A Comprehensive Survey of Methods and Applications) comes from Ming-Hsuan Yang of the University of California & Google Research, Cui Bin Laboratory of Peking University, and CMU and UCLA , Montreal Mila Research Institute and other research teams conducted a comprehensive summary and analysis of the existing diffusion model for the first time, detailing the classification from the diffusion model algorithm, its association with other five major generative models, and its application in seven major fields. The application and other aspects are carried out, and finally the existing limitations and future development directions of the diffusion model are proposed.
Article link: https://arxiv.org/abs/2209.00796 This review of diffusion models paper classification summary github link: https://github.com/YangLing0818/Diffusion -Models-Papers-Survey-Taxonomy
1 Introduction
Diffusion models are new among deep generative models SOTA. The diffusion model surpasses the original SOTA: GAN in the image generation task, and has excellent performance in many application fields, such as computer vision, NLP, waveform signal processing, multi-modal modeling, molecular graph modeling, and time series modeling , antagonistic purification, etc. In addition, diffusion models are closely related to other research fields, such as robust learning, representation learning, and reinforcement learning.
However, the original diffusion model also has shortcomings. Its sampling speed is slow, usually requiring thousands of evaluation steps to draw a sample; its maximum likelihood estimation cannot be compared with likelihood-based estimation. Compared with other models; its ability to generalize to various data types is poor. Nowadays, many studies have made many efforts to solve the above limitations from the perspective of practical applications, or analyzed the model capabilities from a theoretical perspective.
However, there is currently a lack of systematic review of recent advances in diffusion models from algorithms to applications. To reflect the progress in this rapidly growing field, we present the first comprehensive review of diffusion models. We envision that our work will shed light on the design considerations and advanced methods of diffusion models, demonstrate their applications in different fields, and point to future research directions. The summary of this review is shown below:

Although the diffusion model has excellent performance in various tasks, it still has its own Shortcomings, and many studies have improved the diffusion model.
In order to systematically clarify the research progress of diffusion model, we summarized the three main shortcomings of the original diffusion model, which are slow sampling speed, maximum likelihood difference, and weak data generalization ability. It is also proposed to divide the improvement research on diffusion models into three corresponding categories: sampling speed improvement, maximum likelihood enhancement and data generalization enhancement.
We first explain the motivation for improvement, and then further classify the research in each improvement direction according to the characteristics of the method, so as to clearly show the connections and differences between the methods. Here we only select some important methods as examples. Each type of method is introduced in detail in our work, as shown in the figure:

After analyzing the three types of diffusion models, we will introduce the other five generative models GAN, VAE, Autoregressive model, Normalizing flow, and Energy-based model.
Considering the excellent properties of the diffusion model, researchers have combined the diffusion model with other generative models according to its characteristics. Therefore, in order to further demonstrate the characteristics and improvement work of the diffusion model, we detail This article introduces the work of combining diffusion model with other generative models and illustrates the improvements on the original generative model.
Diffusion model has excellent performance in many fields, and considering that diffusion model has different deformations in applications in different fields, we systematically introduced the application research of diffusion model. It includes the following fields: computer vision, NLP, waveform signal processing, multimodal modeling, molecular graph modeling, time series modeling, and adversarial purification. For each task, we define the task and introduce the work that utilizes the diffusion model to handle the task. We summarize the main contributions of this work as follows:
- New classification method: We propose a new, systematic classification method for diffusion models and their applications. Specifically, we divide the models into three categories: sampling speed enhancement, maximum likelihood estimation enhancement, and data generalization enhancement. Furthermore, we classify the applications of diffusion models into seven categories: computer vision, NLP, waveform signal processing, multimodal modeling, molecular graph modeling, time series modeling, and adversarial purification.
- Comprehensive Review: We provide the first comprehensive overview of modern diffusion models and their applications. We present the main improvements for each diffusion model, make necessary comparisons with the original model, and summarize the corresponding papers. For each type of application of diffusion models, we present the main problems that diffusion models address and explain how they solve these problems.
- Future Research Directions: We raise open questions for future research and provide some suggestions for the future development of diffusion models in algorithms and applications.
2 Diffusion model foundation
A core issue in generative modeling is the balance between model flexibility and computability trade-off. The basic idea of the diffusion model is to systematically perturb the distribution in the data through the forward diffusion process, and then restore the distribution of the data by learning the reverse diffusion process, thus producing a highly flexible and easy-to-compute generative model.
(1) Denoising Diffusion Probabilistic Models (DDPM)
A DDPM consists of two parameterized Markov Chain composition and uses variational inference to generate samples consistent with the original data distribution after a finite time. The function of the forward chain is to perturb the data. It gradually adds Gaussian noise to the data according to the pre-designed noise schedule until the distribution of the data tends to the prior distribution, that is, the standard Gaussian distribution. The backward chain starts from a given prior and uses a parameterized Gaussian transformation kernel, learning to gradually restore the original data distribution. represents the original data and its distribution, then the distribution of the forward chain can be expressed by the following formula:

This shows that the forward chain is Markov The process is the sample after adding t steps of noise, and it is the parameter that controls the progress of the noise given in advance. When tends to 1, it can be approximately considered to obey the standard Gaussian distribution. When it is very small, the transfer kernel of the reverse process can be approximately considered to be Gaussian:

We can learn the variational lower bound as a loss function:

## (2) Score-Based Generative Models (SGM)
Above DDPM can be regarded as the discrete form of SGM. SGM constructs a stochastic differential equation (SDE) to smoothly disturb the data distribution and transform the original data distribution into a known prior distribution:

and a corresponding inverse SDE to transform the prior distribution back to the original data distribution:

Therefore, to reverse the diffusion process and generate the data, we The only information required is the fractional function at each time point. Using score-matching techniques we can learn the score function through the following loss function:

For further introduction to the two methods and the relationship between the two, please see our article. The three main shortcomings of the original diffusion model are slow sampling speed, poor likelihood maximization, and weak data generalization ability. Many recent studies have addressed these shortcomings, so we classify improved diffusion models into three categories: sampling speed enhancement, maximum likelihood enhancement, and data generalization enhancement. In the next three, four, and five sections we will introduce these three types of models in detail.
3 Sampling acceleration method
When applied, in order to achieve the best quality of new samples, the diffusion model often needs to be processed thousands of times Ten thousand steps of calculation to obtain a new sample. This limits the practical application value of the diffusion model, because in actual application, we often need to generate a large number of new samples to provide materials for the next step of processing.
Researchers have conducted a lot of research on improving the sampling speed of diffusion model. We describe these studies in detail. We refine it into three methods: Discretization Optimization, Non-Markovian Process, and Partial Sampling.
(1) Discretization Optimization method optimizes the method of solving diffusion SDE. Because solving complex SDE in reality can only use discrete solutions to approximate the real solution, this type of method attempts to optimize the discretization method of SDE to reduce the number of discrete steps while ensuring sample quality. SGM proposes a general method to solve the reverse process, i.e., the same discretization method is adopted for the forward and backward processes. If the forward SDE is given a discretization:

then we can discretize the inverse SDE in the same way:

This method is slightly better than simple DDPM. Furthermore, SGM adds a corrector to the SDE solver so that the samples generated at each step have the correct distribution. At each step of the solution, after the solver is given a sample, the corrector uses a Markov chain Monte Carlo method to correct the distribution of the just-generated sample. Experiments show that adding a corrector to the solver is more efficient than directly increasing the number of steps in the solver.
(2) The Non-Markovian Process method breaks through the limitations of the original Markovian Process. Each step of the reverse process can rely on more past samples to predict new samples, so in Better predictions can also be made with larger step sizes, thus speeding up the sampling process. Among them, DDIM, the main work, no longer assumes that the forward process is a Markov process, but obeys the following distribution:

The sampling process of DDIM can Treated as a discretized divine regular differential equation, the sampling process is more efficient and supports interpolation of samples. Further research found that DDIM can be regarded as a special case of the on-manifold diffusion model PNDM.
(3) The Partial Sampling method directly reduces the sampling time by ignoring a part of the time nodes in the generation process and only using the remaining time nodes to generate samples. For example, Progressive Distillation distills a more efficient diffusion model from a trained diffusion model. For a trained diffusion model, Progressive Distillation will retrain a diffusion model so that one step of the new diffusion model corresponds to the two steps of the trained diffusion model, so that the new model can save half of the sampling process of the old model. The specific algorithm is as follows:

Continuously looping this distillation process can reduce the sampling steps exponentially.
4 Maximum likelihood estimation enhancement
The performance of the diffusion model in maximum likelihood estimation is worse than that of the generative model based on the likelihood function, but the maximum likelihood estimation is better in Many application scenarios are of great significance, such as image compression, semi-supervised learning, and adversarial purification. Since the log-likelihood is difficult to calculate directly, research mainly focuses on optimizing and analyzing variational lower bounds (VLB). We elaborate on models that improve maximum likelihood estimates of diffusion models. We refine it into three categories of methods: Objectives Designing, Noise Schedule Optimization, and Learnable Reverse Variance.
(1) Objectives Designing method uses diffusion SDE to deduce the relationship between the log likelihood of the generated data and the loss function matching the score function. In this way, by appropriately designing the loss function, VLB and log-likelihood can be maximized. Song et al. proved that the weight function of the loss function can be designed so that the likelihood function value of the sample generated by plug-in reverse SDE is less than or equal to the loss function value, that is, the loss function is the upper bound of the likelihood function. The loss function for fractional function fitting is as follows:

We only need to set the weight function to the diffusion coefficient g(t) to make the loss function become The VLB of the likelihood function, that is:

## (2) Noise Schedule Optimization by design or Learn the noisy progress of the forward process to increase VLB. VDM proves that when the discrete steps approach infinity, the loss function is completely determined by the endpoint of the signal-to-noise ratio function SNR(t):

Then in When the discrete steps approach infinity, VLB can be optimized by learning the endpoints of the signal-to-noise ratio function SNR(t), and other aspects of the model can be improved by learning the function values in the middle part of the signal-to-noise ratio function. 3. The Learnable Reverse Variance method learns the variance of the reverse process, thereby reducing fitting errors and can effectively maximize VLB. Analytic-DPM proves that there is an optimal expectation and variance in the reverse process in DDPM and DDIM:

Use the above formula and the trained Fractional function, under the conditions of a given forward process, the optimal VLB can be approximately achieved.
5 Data generalization enhancement
The diffusion model assumes that the data exists in Euclidean space, that is, a manifold with a planar geometry, And adding Gaussian noise will inevitably convert the data into a continuous state space, so the diffusion model can initially only handle continuous data such as pictures, and the effect of directly applying discrete data or other data types is poor. This limits the application scenarios of the diffusion model.
Several research works generalize the diffusion model to other data types, and we explain these methods in detail. We classify it into two types of methods: Feature Space Unification and Data-Dependent Transition Kernels.
(1) The Feature Space Unification method converts the data into a unified latent space, and then diffuses it on the latent space. LSGM proposes to convert the data into a continuous latent space through the VAE framework and then diffuse it on it. The difficulty of this method is how to train VAE and diffusion model at the same time. LSGM shows that since the underlying prior is intractable, the fractional matching loss no longer applies. LSGM directly uses the traditional loss function ELBO in VAE as the loss function, and derives the relationship between ELBO and score matching:

This formula ignores constants established in the sense. By parameterizing the fractional function of the sample in the diffusion process, LSGM can efficiently learn and optimize ELBO.
(2) Data-Dependent Transition Kernels method designs the transition kernels in the diffusion process according to the characteristics of the data type, so that the diffusion model can be directly applied to specific data types. D3PM designed a transition kernel for discrete data, which can be set to lazy random-walk, absorbing state, etc. GEODIFF designed a translation-rotation invariant graph neural network for 3D molecular graph data, and proved that the invariant initial distribution and transition kernel can derive an invariant marginal distribution. Assume it is a translation-rotation transformation, such as:

Then the generated sample distribution also has translation-rotation invariance:

6 Relationship with other generative models
In each section below, we first introduce the other five important types of generation models and analyze their strengths and limitations. We then introduce how diffusion models are related to them and illustrate how these generative models can be improved by incorporating diffusion models. The relationship between VAE, GAN, Autoregressive model, Normalizing flow, Energy-based model and diffusion model is shown in the figure below:

- ##DDPM can be regarded as a hierarchical Markovian VAE (hierarchical Markovian VAE). But there are also differences between DDPM and general VAE. As a VAE, DDPM's encoder and decoder both obey Gaussian distribution and have Markov rows; the dimension of its hidden variables is the same as the data dimension; all layers of the decoder share a neural network.
- DDPM can help GAN solve the problem of unstable training. Because the data is in a low-dimensional manifold in a high-dimensional space, the distribution of the data generated by GAN has a low overlap with the distribution of the real data, resulting in unstable training. The diffusion model provides a process of systematically adding noise. The diffusion model adds noise to the generated data and real data, and then sends the noise-added data to the discriminator. This can effectively solve the problem of GAN being unable to train and the training being unstable. .
- Normalizing flow converts data to a priori distribution through a bijection function. This approach limits the expression ability of Normalizing flow, resulting in poor application results. The analogy diffusion model adds noise to the encoder, which can increase the expression ability of Normalizing flow. From another perspective, this approach is to extend the diffusion model to a model that can also be learned in the forward process.
- Autoregressive model needs to ensure that the data has a certain structure, which makes it very difficult to design and parameterize the autoregressive model. The training of diffusion models inspired the training of autoregressive models, which avoids design difficulties through specific training methods.
- Energy-based model directly models the distribution of original data, but direct modeling makes learning and sampling difficult. By using diffusion recovery likelihood, the model can first add slight noise to the sample, and then infer the distribution of the original sample from the slightly noisy sample distribution, making the learning and sampling process simpler and more stable.
7 Application of Diffusion Model
In this section, we introduce the application of diffusion model in computer vision and natural language processing respectively. , waveform signal processing, multi-modal learning, molecular graph generation, time series and adversarial learning, etc. Applications in seven major application directions, and the methods in each type of application are subdivided and analyzed. For example, in computer vision, diffusion model can be used for image completion and repair (RePaint):

In multi-modal tasks, diffusion model can be used Text-to-image generation (GLIDE):

You can also use diffusion model to generate drug molecules and protein molecules in molecular graph generation (GeoDiff ):

Application classification summary is shown in the table:

##8 Future Research Directions
- Apply hypothesis re-testing. We need to examine the generally accepted assumptions we make in our applications. For example, in practice, it is generally believed that the forward process of the diffusion model will transform the data into a standard Gaussian distribution, but this is not the case. More forward diffusion steps will make the final sample distribution closer to the standard Gaussian distribution, consistent with the sampling process. ; but more forward diffusion steps also make estimating the fractional function more difficult. Theoretical conditions are difficult to obtain, thus leading to a mismatch between theory and practice in practice. We should be aware of this situation and design appropriate diffusion models.
- From discrete time to continuous time. Due to the flexibility of diffusion models, many empirical methods can be enhanced with further analysis. This research idea is promising by converting discrete-time models into corresponding continuous-time models and then designing more and better discrete methods.
- New generation process. Diffusion models generate samples through two main methods: one is to discretize the inverse diffusion SDE, and then generate the samples through the discretized inverse SDE; the other is to use the Markov properties of the inverse process to progressively denoise the samples. However, for some tasks, it is difficult to apply these methods to generate samples in practice. Therefore, further research into new generative processes and perspectives is needed.
- Generalize to more complex scenarios and more research areas. Although the diffusion model has been applied to many scenarios, most of them are limited to single-input and single-output scenarios. In the future, you can consider applying it to more complex scenarios, such as text-to-audiovisual speech synthesis. You can also consider combining it with more research fields.
The above is the detailed content of The recently popular Diffusion Model, the first review of diffusion generation models!. For more information, please follow other related articles on the PHP Chinese website!
 What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AM
What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AMIntroduction In prompt engineering, “Graph of Thought” refers to a novel approach that uses graph theory to structure and guide AI’s reasoning process. Unlike traditional methods, which often involve linear s
 Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AM
Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AMIntroduction Congratulations! You run a successful business. Through your web pages, social media campaigns, webinars, conferences, free resources, and other sources, you collect 5000 email IDs daily. The next obvious step is
 Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AM
Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AMIntroduction In today’s fast-paced software development environment, ensuring optimal application performance is crucial. Monitoring real-time metrics such as response times, error rates, and resource utilization can help main
 ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM
ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM“How many users do you have?” he prodded. “I think the last time we said was 500 million weekly actives, and it is growing very rapidly,” replied Altman. “You told me that it like doubled in just a few weeks,” Anderson continued. “I said that priv
 Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AM
Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AMIntroduction Mistral has released its very first multimodal model, namely the Pixtral-12B-2409. This model is built upon Mistral’s 12 Billion parameter, Nemo 12B. What sets this model apart? It can now take both images and tex
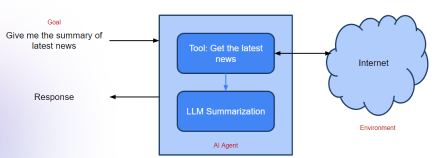 Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AM
Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AMImagine having an AI-powered assistant that not only responds to your queries but also autonomously gathers information, executes tasks, and even handles multiple types of data—text, images, and code. Sounds futuristic? In this a
 Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AM
Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AMIntroduction The finance industry is the cornerstone of any country’s development, as it drives economic growth by facilitating efficient transactions and credit availability. The ease with which transactions occur and credit
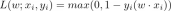 Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AM
Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AMIntroduction Data is being generated at an unprecedented rate from sources such as social media, financial transactions, and e-commerce platforms. Handling this continuous stream of information is a challenge, but it offers an


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function

SublimeText3 Linux new version
SublimeText3 Linux latest version

SublimeText3 Chinese version
Chinese version, very easy to use




