Detailed tutorial on drawing three-dimensional graphs in python-Python Tutorial-php.cn

Home

Backend Development

Python Tutorial

Detailed tutorial on drawing three-dimensional graphs in python

WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB

Aug 30, 2022 pm 12:04 PM

python

This article brings you relevant knowledge about Python. Usually we use Python to draw two-dimensional plane diagrams, but sometimes we also need to draw three-dimensional scene diagrams. The following is an introduction to python drawing I hope this information about three-dimensional drawings will be helpful to everyone.

Detailed tutorial on drawing three-dimensional graphs in python

[Related recommendations: Python3 video tutorial]

This article only summarizes the most basic drawing methods.

1. Initialization

Assume that the matplotlib tool package has been installed.

Use matplotlib.figure.Figure to create a plot frame:

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection=&#39;3d&#39;)

2. Line plots

Basic usage:

ax.plot(x,y,z,label=&#39; &#39;)

code:

import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
 
mpl.rcParams[&#39;legend.fontsize&#39;] = 10
 
fig = plt.figure()
ax = fig.gca(projection=&#39;3d&#39;)
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
z = np.linspace(-2, 2, 100)
r = z**2 + 1
x = r * np.sin(theta)
y = r * np.cos(theta)
ax.plot(x, y, z, label=&#39;parametric curve&#39;)
ax.legend()
 
plt.show()

3. Scatter plots

Basic usage:

ax.scatter(xs, ys, zs, s=20, c=None, depthshade=True, *args, *kwargs)

xs,ys,zs: input data;
s: size of scatter point
c: color, such as c = 'r' is red;
depthshase : Transparent, True is transparent, the default is True, False is opaque
*args, etc. are expansion variables, such as maker = 'o', then the scatter result is the shape of 'o'

code:

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
 
 
def randrange(n, vmin, vmax):
    &#39;&#39;&#39;
    Helper function to make an array of random numbers having shape (n, )
    with each number distributed Uniform(vmin, vmax).
    &#39;&#39;&#39;
    return (vmax - vmin)*np.random.rand(n) + vmin
 
fig = plt.figure()
ax = fig.add_subplot(111, projection=&#39;3d&#39;)
 
n = 100
 
# For each set of style and range settings, plot n random points in the box
# defined by x in [23, 32], y in [0, 100], z in [zlow, zhigh].
for c, m, zlow, zhigh in [(&#39;r&#39;, &#39;o&#39;, -50, -25), (&#39;b&#39;, &#39;^&#39;, -30, -5)]:
    xs = randrange(n, 23, 32)
    ys = randrange(n, 0, 100)
    zs = randrange(n, zlow, zhigh)
    ax.scatter(xs, ys, zs, c=c, marker=m)
 
ax.set_xlabel(&#39;X Label&#39;)
ax.set_ylabel(&#39;Y Label&#39;)
ax.set_zlabel(&#39;Z Label&#39;)
 
plt.show()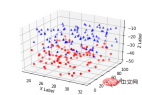

4. Wireframe plots

Basic usage:

ax.plot_wireframe(X, Y, Z, *args, **kwargs)

X, Y, Z: Input data
rstride: row step length
cstride: column step length
rcount: upper limit of row number
ccount: upper limit of column number

code:

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
 
 
fig = plt.figure()
ax = fig.add_subplot(111, projection=&#39;3d&#39;)
 
# Grab some test data.
X, Y, Z = axes3d.get_test_data(0.05)
 
# Plot a basic wireframe.
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)
 
plt.show()

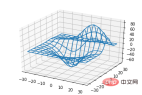
5. Surface plots

Basic usage:

ax.plot_surface(X, Y, Z, *args, **kwargs)

X,Y,Z: data
rstride, cstride, rcount, ccount: same as Wireframe plots definition
color: surface color
cmap: layer

code:

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
import numpy as np
 
 
fig = plt.figure()
ax = fig.gca(projection=&#39;3d&#39;)
 
# Make data.
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
 
# Plot the surface.
surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm,
                       linewidth=0, antialiased=False)
 
# Customize the z axis.
ax.set_zlim(-1.01, 1.01)
ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter(FormatStrFormatter(&#39;%.02f&#39;))
 
# Add a color bar which maps values to colors.
fig.colorbar(surf, shrink=0.5, aspect=5)
 
plt.show()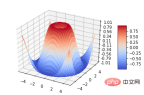

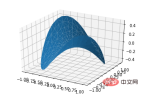
6. Tri-Surface plots

Basic usage:

ax.plot_trisurf(*args, **kwargs)

X,Y,Z: data
Other parameters are similar to surface-plot

code:

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
 
 
n_radii = 8
n_angles = 36
 
# Make radii and angles spaces (radius r=0 omitted to eliminate duplication).
radii = np.linspace(0.125, 1.0, n_radii)
angles = np.linspace(0, 2*np.pi, n_angles, endpoint=False)
 
# Repeat all angles for each radius.
angles = np.repeat(angles[..., np.newaxis], n_radii, axis=1)
 
# Convert polar (radii, angles) coords to cartesian (x, y) coords.
# (0, 0) is manually added at this stage,  so there will be no duplicate
# points in the (x, y) plane.
x = np.append(0, (radii*np.cos(angles)).flatten())
y = np.append(0, (radii*np.sin(angles)).flatten())
 
# Compute z to make the pringle surface.
z = np.sin(-x*y)
 
fig = plt.figure()
ax = fig.gca(projection=&#39;3d&#39;)
 
ax.plot_trisurf(x, y, z, linewidth=0.2, antialiased=True)
 
plt.show()

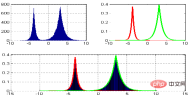
7. Contour plots

Basic usage:

ax.contour(X, Y, Z, *args, **kwargs)

code:

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import cm
 
fig = plt.figure()
ax = fig.add_subplot(111, projection=&#39;3d&#39;)
X, Y, Z = axes3d.get_test_data(0.05)
cset = ax.contour(X, Y, Z, cmap=cm.coolwarm)
ax.clabel(cset, fontsize=9, inline=1)
 
plt.show()

##Two-dimensional contours Lines can also be drawn together with a three-dimensional surface map:

code:

from mpl_toolkits.mplot3d import axes3d
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import cm
 
fig = plt.figure()
ax = fig.gca(projection=&#39;3d&#39;)
X, Y, Z = axes3d.get_test_data(0.05)
ax.plot_surface(X, Y, Z, rstride=8, cstride=8, alpha=0.3)
cset = ax.contour(X, Y, Z, zdir=&#39;z&#39;, offset=-100, cmap=cm.coolwarm)
cset = ax.contour(X, Y, Z, zdir=&#39;x&#39;, offset=-40, cmap=cm.coolwarm)
cset = ax.contour(X, Y, Z, zdir=&#39;y&#39;, offset=40, cmap=cm.coolwarm)
 
ax.set_xlabel(&#39;X&#39;)
ax.set_xlim(-40, 40)
ax.set_ylabel(&#39;Y&#39;)
ax.set_ylim(-40, 40)
ax.set_zlabel(&#39;Z&#39;)
ax.set_zlim(-100, 100)
 
plt.show()

It can also be the projection of a three-dimensional contour line on a two-dimensional plane:

code:

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import cm
 
fig = plt.figure()
ax = fig.gca(projection=&#39;3d&#39;)
X, Y, Z = axes3d.get_test_data(0.05)
ax.plot_surface(X, Y, Z, rstride=8, cstride=8, alpha=0.3)
cset = ax.contourf(X, Y, Z, zdir=&#39;z&#39;, offset=-100, cmap=cm.coolwarm)
cset = ax.contourf(X, Y, Z, zdir=&#39;x&#39;, offset=-40, cmap=cm.coolwarm)
cset = ax.contourf(X, Y, Z, zdir=&#39;y&#39;, offset=40, cmap=cm.coolwarm)
 
ax.set_xlabel(&#39;X&#39;)
ax.set_xlim(-40, 40)
ax.set_ylabel(&#39;Y&#39;)
ax.set_ylim(-40, 40)
ax.set_zlabel(&#39;Z&#39;)
ax.set_zlim(-100, 100)
 
plt.show()

8. Bar plots (bar chart)

Basic usage:

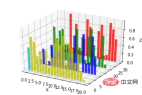
ax.bar(left, height, zs=0, zdir=&#39;z&#39;, *args, **kwargs

zdir: The direction of the bar chart planarization, the specific code can be understood accordingly.

code:

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
 
fig = plt.figure()
ax = fig.add_subplot(111, projection=&#39;3d&#39;)
for c, z in zip([&#39;r&#39;, &#39;g&#39;, &#39;b&#39;, &#39;y&#39;], [30, 20, 10, 0]):
    xs = np.arange(20)
    ys = np.random.rand(20)
 
    # You can provide either a single color or an array. To demonstrate this,
    # the first bar of each set will be colored cyan.
    cs = [c] * len(xs)
    cs[0] = &#39;c&#39;
    ax.bar(xs, ys, zs=z, zdir=&#39;y&#39;, color=cs, alpha=0.8)
 
ax.set_xlabel(&#39;X&#39;)
ax.set_ylabel(&#39;Y&#39;)
ax.set_zlabel(&#39;Z&#39;)
 
plt.show()

9. Subplot drawing (subplot)

A-different 2-D graphics, Distributed in 3-D space, in fact, the projection space is not empty, corresponding code:

from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
 
fig = plt.figure()
ax = fig.gca(projection=&#39;3d&#39;)
 
# Plot a sin curve using the x and y axes.
x = np.linspace(0, 1, 100)
y = np.sin(x * 2 * np.pi) / 2 + 0.5
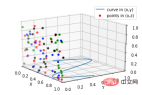
ax.plot(x, y, zs=0, zdir=&#39;z&#39;, label=&#39;curve in (x,y)&#39;)
 
# Plot scatterplot data (20 2D points per colour) on the x and z axes.
colors = (&#39;r&#39;, &#39;g&#39;, &#39;b&#39;, &#39;k&#39;)
x = np.random.sample(20*len(colors))
y = np.random.sample(20*len(colors))
c_list = []
for c in colors:
    c_list.append([c]*20)
# By using zdir=&#39;y&#39;, the y value of these points is fixed to the zs value 0
# and the (x,y) points are plotted on the x and z axes.
ax.scatter(x, y, zs=0, zdir=&#39;y&#39;, c=c_list, label=&#39;points in (x,z)&#39;)
 
# Make legend, set axes limits and labels
ax.legend()
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.set_zlim(0, 1)
ax.set_xlabel(&#39;X&#39;)
ax.set_ylabel(&#39;Y&#39;)
ax.set_zlabel(&#39;Z&#39;)

B-subgraph Subplot usage

The difference from MATLAB is , if a four-subgraph effect, such as:

##MATLAB:

subplot(2,2,1)
subplot(2,2,2)
subplot(2,2,[3,4])

Python:

subplot(2,2,1)
subplot(2,2,2)
subplot(2,1,2)

code:

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D, get_test_data
from matplotlib import cm
import numpy as np
 
 
# set up a figure twice as wide as it is tall
fig = plt.figure(figsize=plt.figaspect(0.5))
 
#===============
#  First subplot
#===============
# set up the axes for the first plot
ax = fig.add_subplot(2, 2, 1, projection=&#39;3d&#39;)
 
# plot a 3D surface like in the example mplot3d/surface3d_demo
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm,
                       linewidth=0, antialiased=False)
ax.set_zlim(-1.01, 1.01)
fig.colorbar(surf, shrink=0.5, aspect=10)
 
#===============
# Second subplot
#===============
# set up the axes for the second plot
ax = fig.add_subplot(2,1,2, projection=&#39;3d&#39;)
 
# plot a 3D wireframe like in the example mplot3d/wire3d_demo
X, Y, Z = get_test_data(0.05)
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)
 
plt.show()

Supplement:

Basic usage of text comments:

code:

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
 
 
fig = plt.figure()
ax = fig.gca(projection=&#39;3d&#39;)
 
# Demo 1: zdir
zdirs = (None, &#39;x&#39;, &#39;y&#39;, &#39;z&#39;, (1, 1, 0), (1, 1, 1))
xs = (1, 4, 4, 9, 4, 1)
ys = (2, 5, 8, 10, 1, 2)
zs = (10, 3, 8, 9, 1, 8)
 
for zdir, x, y, z in zip(zdirs, xs, ys, zs):
    label = &#39;(%d, %d, %d), dir=%s&#39; % (x, y, z, zdir)
    ax.text(x, y, z, label, zdir)
 
# Demo 2: color
ax.text(9, 0, 0, "red", color=&#39;red&#39;)
 
# Demo 3: text2D
# Placement 0, 0 would be the bottom left, 1, 1 would be the top right.
ax.text2D(0.05, 0.95, "2D Text", transform=ax.transAxes)
 
# Tweaking display region and labels
ax.set_xlim(0, 10)
ax.set_ylim(0, 10)
ax.set_zlim(0, 10)
ax.set_xlabel(&#39;X axis&#39;)
ax.set_ylabel(&#39;Y axis&#39;)
ax.set_zlabel(&#39;Z axis&#39;)
 
plt.show()

##【 Related recommendations: Python3 video tutorial

】

The above is the detailed content of Detailed tutorial on drawing three-dimensional graphs in python. For more information, please follow other related articles on the PHP Chinese website!

Statement

This article is reproduced at:脚本之家. If there is any infringement, please contact admin@php.cn delete

How to implement factory model in Python?May 16, 2025 pm 12:39 PM

Implementing factory pattern in Python can create different types of objects by creating a unified interface. The specific steps are as follows: 1. Define a basic class and multiple inheritance classes, such as Vehicle, Car, Plane and Train. 2. Create a factory class VehicleFactory and use the create_vehicle method to return the corresponding object instance according to the type parameter. 3. Instantiate the object through the factory class, such as my_car=factory.create_vehicle("car","Tesla"). This pattern improves the scalability and maintainability of the code, but it needs to be paid attention to its complexity

What does r mean in python original string prefixMay 16, 2025 pm 12:36 PM

In Python, the r or R prefix is used to define the original string, ignoring all escaped characters, and letting the string be interpreted literally. 1) Applicable to deal with regular expressions and file paths to avoid misunderstandings of escape characters. 2) Not applicable to cases where escaped characters need to be preserved, such as line breaks. Careful checking is required when using it to prevent unexpected output.

How to clean up resources using the __del__ method in Python?May 16, 2025 pm 12:33 PM

In Python, the __del__ method is an object's destructor, used to clean up resources. 1) Uncertain execution time: Relying on the garbage collection mechanism. 2) Circular reference: It may cause the call to be unable to be promptly and handled using the weakref module. 3) Exception handling: Exception thrown in __del__ may be ignored and captured using the try-except block. 4) Best practices for resource management: It is recommended to use with statements and context managers to manage resources.

Usage of pop() function in python list pop element removal method detailed explanation of theMay 16, 2025 pm 12:30 PM

The pop() function is used in Python to remove elements from a list and return a specified position. 1) When the index is not specified, pop() removes and returns the last element of the list by default. 2) When specifying an index, pop() removes and returns the element at the index position. 3) Pay attention to index errors, performance issues, alternative methods and list variability when using it.

How to use Python for image processing?May 16, 2025 pm 12:27 PM

Python mainly uses two major libraries Pillow and OpenCV for image processing. Pillow is suitable for simple image processing, such as adding watermarks, and the code is simple and easy to use; OpenCV is suitable for complex image processing and computer vision, such as edge detection, with superior performance but attention to memory management is required.

How to implement principal component analysis in Python?May 16, 2025 pm 12:24 PM

Implementing PCA in Python can be done by writing code manually or using the scikit-learn library. Manually implementing PCA includes the following steps: 1) centralize the data, 2) calculate the covariance matrix, 3) calculate the eigenvalues and eigenvectors, 4) sort and select principal components, and 5) project the data to the new space. Manual implementation helps to understand the algorithm in depth, but scikit-learn provides more convenient features.

How to calculate logarithm in Python?May 16, 2025 pm 12:21 PM

Calculating logarithms in Python is a very simple but interesting thing. Let's start with the most basic question: How to calculate logarithm in Python? Basic method of calculating logarithm in Python The math module of Python provides functions for calculating logarithm. Let's take a simple example: importmath# calculates the natural logarithm (base is e) x=10natural_log=math.log(x)print(f"natural log({x})={natural_log}")# calculates the logarithm with base 10 log_base_10=math.log10(x)pri

How to implement linear regression in Python?May 16, 2025 pm 12:18 PM

To implement linear regression in Python, we can start from multiple perspectives. This is not just a simple function call, but involves a comprehensive application of statistics, mathematical optimization and machine learning. Let's dive into this process in depth. The most common way to implement linear regression in Python is to use the scikit-learn library, which provides easy and efficient tools. However, if we want to have a deeper understanding of the principles and implementation details of linear regression, we can also write our own linear regression algorithm from scratch. The linear regression implementation of scikit-learn uses scikit-learn to encapsulate the implementation of linear regression, allowing us to easily model and predict. Here is a use sc

See all articles