What is the picture in php? How can it be stored?

With the deepening of learning, our knowledge is constantly expanding and enriching. Has the tree structure confused everyone? Believe me, after learning the diagram, you will feel that binary trees are simply indescribably simple. In fact, the tree we are talking about is also a special form of graph.

The concept of pictures

Do you still remember the picture of a tree we saw in the first article about learning trees?

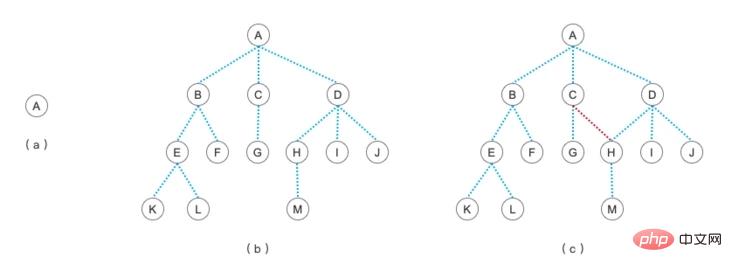
At that time, we said that picture c is not a tree, but a picture. why? From the definition of tree, we can see that a tree can only have one root node, there can be no connection between levels, and it can have multiple child nodes. Graphs do not have to follow these rules. The characteristic of graphs is that nodes can be connected to each other. For example, the pictures below are all pictures.

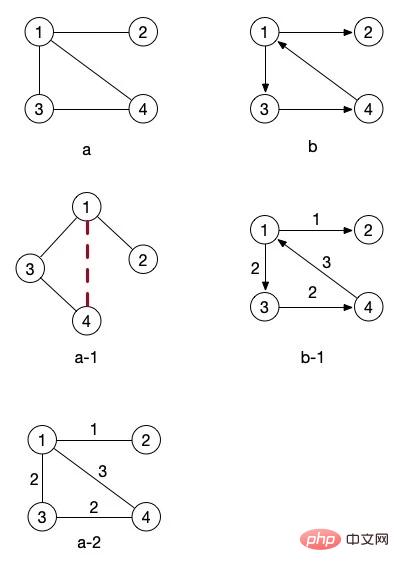
In the picture drawn above, picture b has an arrow, while the connecting line in picture a has no arrow. It has a clear direction like this. The graph is called a directed graph. A graph without arrows, that is, a graph with no direction, is called an undirected graph.

Let’s first move our attention to Figure a-1. In fact, it just rotates Figure a. Can everyone see it? If you ignore the connection between nodes 4 and 1, then it is a tree. Is it consistent with the concept of Figure c in our tree diagram above?

The more formal official definition of graph is:

Graph (Graph) G consists of two sets V and E, recorded as G=(V, E), where V is the vertex The finite non-empty set of E is the finite set of vertices in V. Even pairs of these vertices are called edges.

In a directed graph, the line segment connecting two points from the starting node to the pointing node can be recorded as . and are two different sides, which can also be called arcs. According to Figure a, we can see that there are , , , , , , , these edges. In Figure b, because it is a directed graph, it only has four edges: , , , .

Do you feel that it is clearer when you look at the picture above, but you are confused when you look at this definition? If you are a student who needs to take a test, you still have to memorize this definition. If you just want to focus on learning, application or understanding like me, there is no need to memorize it by rote. V is the node, E is the relationship between these nodes, the relationship between two vertices, that is, the line segments connecting the nodes on the graph are the edges.

OK, now that these three most basic concepts are understood, let’s continue to learn other terminology related to pictures!

Terms related to graphs

First of all, we use n to represent the number of vertices in the graph, and e to represent the number of edges. Remember these two codes.

• (1) Subgraph: Suppose there are two graphs G=(V, E) and G'=(V', E') if V' is contained in V and E' Contained in E, then G' is called a subgraph of G

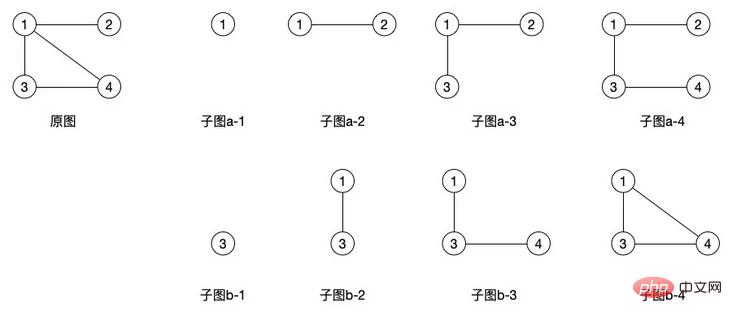
The subgraphs on the right in the above figure are all subgraphs of the original figure , it can be seen that subgraphs can generate a lot of shapes, and directed graphs have the same concept. However, compared to undirected graphs, directed graphs can generate fewer subgraphs because its edges are directional. .

• (2) Undirected complete graph and directed complete graph: For an undirected graph, if it has n(n-1)/2 edges, it is an undirected complete graph. For a directed graph, if it has n(n-1) orphans, it is called a directed complete graph. (Refer to the complete binary tree)

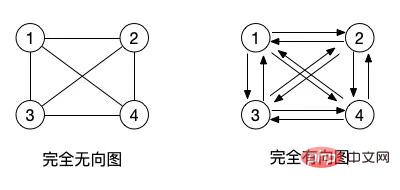
In fact, the concept of a complete graph is that all adjacent nodes in the graph have edges that can connect them together.

For directed graphs, although the edges are directional, of course we can also define a back-and-forth direction, such as and , in a directed graph We have to draw two arrows in opposite directions to indicate that it can go from 1 to 2 or from 2 to 1. In undirected graphs, one edge is used to replace the concept of these two edges. The edge without an arrow direction is bidirectional.

• (3) Sparse graph and dense graph: A graph with few edges or orphans (such as e

• (4) Quanhe Net: In practical applications, each edge or island can be marked with a value that has some meaning, just like the distance on a map. These values ​​are called weights. A picture with authority can be called a network

The numbers on the sides of Figure a-2 and Figure b-1 in the top pictures represent the weights. These two pictures can be called network pictures. We will learn the concept of weight later when we talk about related algorithms. From these two pictures, we can actually clearly see that if we want to go from node 1 to node 4, we do not go directly to this side, but it is faster to take the , route.

• (5) Adjacent points: Two nodes with edges are adjacent points

• (6) Degree, in-degree and out-degree : The degree of vertex v refers to the number of edges associated with v. For a directed graph, the arrow pointing to other nodes is the out-degree, and the arrow pointing to itself is the in-degree

Let’s continue looking at Figure b. Node 1 has two out-degrees and one in-degree. This doesn’t seem to require much explanation.

• (7) Path and path length: All the vertices passing from one vertex to another vertex are paths. If it is a directed graph, then its path is in the direction of the arrow. The path length is the number of edges or orphans passing through on a path

• (8) Loop or loop: A path whose first vertex and last vertex are the same is called a loop or loop

• (9) Connectivity, connected graph and connected components: If there is a path between two nodes, they are said to be connected. If all nodes in the entire graph can be connected to each other, then the graph is a connected graph. A connected component is a maximal connected subgraph in an undirected graph.

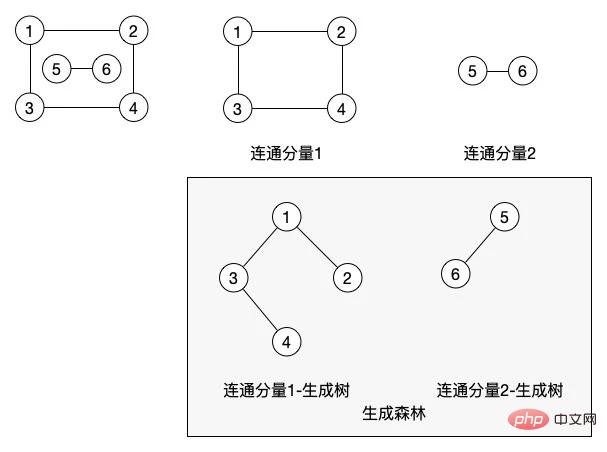
The following three concepts are also given in this picture. In an undirected graph, a connected component is equal to a maximal connected subgraph. In this graph, we have two connected components.

• (10) Maximally connected subgraph: The maximum number of nodes that a connected subgraph can contain. If one more node is added, the subgraph will not be a connected graph

• (11) Spanning tree: a minimal connected subgraph, which contains all the vertices in the graph, but only n-1 edges that are enough to form a tree. Such a connected subgraph is The spanning tree of a connected graph

# is actually a path that connects all the nodes in the graph. In the graph of connected components, we generate two minimum spanning trees based on the two connected components. The nodes of the spanning tree of their connected component 1 do not necessarily have to be in this structure. We can put node 4 under node 2, depending on how we traverse to generate this minimum spanning tree.

The minimum spanning tree of our top figure a can actually be Figure a-1 without the red dotted line. Of course, node 4 can also be placed under node 1. It also depends on how our program traverses the graph to generate what kind of tree.

• (12) Spanning forest: In a non-connected graph, each connected component can generate a connected spanning tree, thus forming the spanning forest of the entire non-connected graph

Are you dizzy after reading this? It doesn't matter, we will use these terms frequently in subsequent studies, and this is not the most comprehensive. You can use the bibliography and other learning materials to have a more in-depth study and understanding of graph-related terminology.

Summary

The concept of graphs is almost introduced. You can digest it and continue to learn the following content. This is just the beginning. Many students will feel that this thing has improved a lot compared to the tree structure. Don't be afraid, after learning the following knowledge, even if you haven't figured out the content related to graph yet, you will definitely have a deeper understanding of the tree structure. why? Trees are actually graphs without loops. Their traversal is achieved through depth or breadth, but the graph is more complicated. Now, do you feel that there is still some hope for the future? Learning is often a gradual process. There will always be a connection between current knowledge and past knowledge. Don’t think too much first, just go on step by step!

Recommendation: 《2021 PHP interview questions summary (collection)》《php video tutorial》

The above is the detailed content of What is the picture in php? How can it be stored?. For more information, please follow other related articles on the PHP Chinese website!