Transaction number TID |
Items purchased by customers |
Transaction number TID |
Item purchased by the customer |
T1 |
bread, cream, milk, tea |
T6 |
bread, tea |
T2 |
bread, cream, milk |
T7 |
beer, milk, tea
|
T3 |
cake, milk |
T8 |
bread, tea |
| ##T4
|
milk, tea
|
T9
|
bread, cream, milk, tea
|
##T5 | bread, cake, milk | T10 | bread, milk , tea |
Definition 1: Let I={i1,i2,…,im}, which is a set of m different items, each ik is called For a project. The collection I of items is called itemset. The number of its elements is called the length of the itemset, and an itemset of length k is called a k-itemset. In the example, each product is an item, the itemset is I={bread, beer, cake,cream, milk, tea}, and the length of I is 6.
Definition 2: Each transactionT is a child of the itemset I set. Corresponding to each transaction, there is a unique identification transaction number, recorded as TID. All transactions constitute Transaction databaseD, |D| is equal to the number of transactions in D. The example contains 10 transactions, so |D|=10.
Definition 3: For itemset X, set count(X⊆T) to the number of transactions containing X in transaction set D quantity, then the support of the itemset X is:
support(X)=count(X⊆T)/|D|
In the example, X={bread, milk} appears in T1, T2, T5, T9 and T10, so the support is 0.5.
Definition 4: Minimum support is the minimum of the itemset The support threshold, recorded as SUPmin, represents the minimum importance of association rules that users care about. Item sets whose support is not less than SUPmin are called frequent sets , and frequent sets with length k are called k-frequent sets. If SUPmin is set to 0.3, the support of {bread, milk} in the example is 0.5, so it is a 2-frequent set.
Definition 5: Association rule is an implication:
R:X⇒Y
whereX⊂I, Y⊂I, and X∩Y=⌀. Indicates that if itemset X appears in a certain transaction, Y will also appear with a certain probability. Association rules that users care about can be measured by two standards: support and credibility.
Definition 6: The support of association rule R is a transaction The ratio of the number of transactions in the set containing both X and Y to |D|. That is: support(X⇒Y)=count(X⋃Y)/|D|
Support reflects the probability that X and Y appear at the same time. The support of association rules is equal to the support of frequent sets.
Definition 7
: For association rule R, credibility It refers to the ratio of the number of transactions containing X and Y to the number of transactions containing X. That is: confidence(X⇒Y)=support(X⇒Y)/support(X)
Confidence reflects that if X is included in the transaction, then The probability that the transaction contains Y. Generally speaking, only association rules with high support and credibility are of interest to users.
Definition 8: Set the minimum support and minimum credibility of association rules as SUPmin and CONFmin. If the support and credibility of rule R are not less than SUPmin and CONFmin, it is called
strong association rule. The purpose of association rule mining is to find strong association rules to guide merchants' decision-making. These eight definitions include several important basic concepts related to association rules. There are two main problems in association rule mining:
- Find all frequent itemsets in the transaction database that are greater than or equal to the minimum support specified by the user.
- Use frequent item sets to generate the required association rules, and filter out strong association rules based on the minimum credibility set by the user.
Currently, researchers are mainly focusing on the first problem. It is difficult to find frequent sets, but it is relatively easy to generate strong association rules with frequent sets.
2. Theoretical basis
First let’s look at the properties of a frequent set.
Theorem: If the itemset X is a frequent set, then its non-empty subsets are all frequent sets .
According to the theorem, given an itemset X of a k-frequent set, all k-1 order subsets of The itemsets of two k-1 frequent sets differ only in one item and are equal to X after being connected. This proves that the k-candidate set generated by concatenating k-1 frequent sets covers the k-frequent set. At the same time, if the itemset Y in the k-candidate set contains a k-1 order subset that does not belong to the k-1 frequent set, then Y cannot be a frequent set and should be pruned from the candidate set. The Apriori algorithm takes advantage of this property of frequent sets.
3. Algorithm steps:
First is the test data:
TransactionID |
ProductIDList |
T100 |
I1, I2, I5 |
| T200
|
I2,I4 |
| ##T300
|
I2, I3
|
##T400 | I1, I2, I4 |
T500 | I1, I3 |
T600 | I2,I3 |
T700 | #I1,I3
|
T800 | I1, I2, I3, I5 |
##T900
|
I1, I2, I3 |
|
Step diagram of the algorithm:
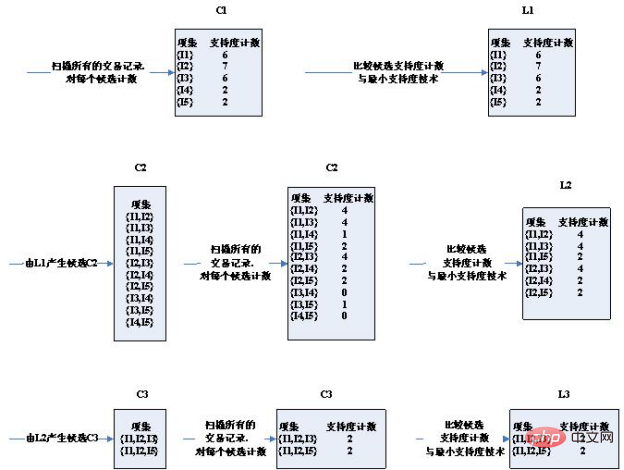
As you can see, the third round of candidate sets has occurred Significantly reduced, why is this?
Please note the two conditions for selecting candidate sets:
1. The two conditions for two K itemsets to be connected are that they have K- 1 item is the same. Therefore, (I2, I4) and (I3, I5) cannot be connected. The candidate set is narrowed.
2. If an itemset is a frequent set, then it does not have a frequent set that is not a subset. For example, (I1, I2) and (I1, I4) get (I1, I2, I4), and the subset (I1, I4) of (I1, I2, I4) is not a frequent set. The candidate set is narrowed.
The support of the 2 candidate sets obtained in the third round is exactly equal to the minimum support. Therefore, they are all included in frequent sets.
Now look at the candidate set and frequent set results of the fourth round is empty
You can see that the candidate set and The frequent set is actually empty! Because the frequent sets obtained through the third round are self-connected to get {I1, I2, I3, I5}, which has the subset {I2, I3, I5}, and {I2, I3, I5} is not a frequent set, and is not It satisfies the condition that a subset of frequent sets is also a frequent set, so it is cut off by pruning. Therefore, the entire algorithm is terminated, and the frequent set obtained by the last calculation is taken as the final frequent set result:
That is: ['I1,I2,I3', 'I1,I2,I5 ']
4. Code:
Write Python code to implement the Apriori algorithm. The code needs to pay attention to the following two points:
- Since the Apriori algorithm assumes that the items in the itemset are sorted in lexicographic order, and the set itself is unordered, we need to perform set and list when necessary. Conversion;
- Since a dictionary (support_data) is used to record the support of an item set, the item set needs to be used as the key, and the variable set cannot be used as the key of the dictionary, so the item set should be converted to fixed at the appropriate time. Collection frozenset.
def local_data(file_path): import pandas as pd
dt = pd.read_excel(file_path)
data = dt['con']
locdata = [] for i in data:
locdata.append(str(i).split(",")) # print(locdata) # change to [[1,2,3],[1,2,3]]
length = [] for i in locdata:
length.append(len(i)) # 计算长度并存储
# print(length)
ki = length[length.index(max(length))] # print(length[length.index(max(length))]) # length.index(max(length)读取最大值的位置,然后再定位取出最大值
return locdata,kidef create_C1(data_set): """
Create frequent candidate 1-itemset C1 by scaning data set.
Args:
data_set: A list of transactions. Each transaction contains several items.
Returns:
C1: A set which contains all frequent candidate 1-itemsets """
C1 = set() for t in data_set: for item in t:
item_set = frozenset([item])
C1.add(item_set) return C1def is_apriori(Ck_item, Lksub1): """
Judge whether a frequent candidate k-itemset satisfy Apriori property.
Args:
Ck_item: a frequent candidate k-itemset in Ck which contains all frequent
candidate k-itemsets.
Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets.
Returns:
True: satisfying Apriori property.
False: Not satisfying Apriori property. """
for item in Ck_item:
sub_Ck = Ck_item - frozenset([item]) if sub_Ck not in Lksub1: return False return Truedef create_Ck(Lksub1, k): """
Create Ck, a set which contains all all frequent candidate k-itemsets
by Lk-1's own connection operation.
Args:
Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets.
k: the item number of a frequent itemset.
Return:
Ck: a set which contains all all frequent candidate k-itemsets. """
Ck = set()
len_Lksub1 = len(Lksub1)
list_Lksub1 = list(Lksub1) for i in range(len_Lksub1): for j in range(1, len_Lksub1):
l1 = list(list_Lksub1[i])
l2 = list(list_Lksub1[j])
l1.sort()
l2.sort() if l1[0:k-2] == l2[0:k-2]:
Ck_item = list_Lksub1[i] | list_Lksub1[j] # pruning
if is_apriori(Ck_item, Lksub1):
Ck.add(Ck_item) return Ckdef generate_Lk_by_Ck(data_set, Ck, min_support, support_data): """
Generate Lk by executing a delete policy from Ck.
Args:
data_set: A list of transactions. Each transaction contains several items.
Ck: A set which contains all all frequent candidate k-itemsets.
min_support: The minimum support.
support_data: A dictionary. The key is frequent itemset and the value is support.
Returns:
Lk: A set which contains all all frequent k-itemsets. """
Lk = set()
item_count = {} for t in data_set: for item in Ck: if item.issubset(t): if item not in item_count:
item_count[item] = 1 else:
item_count[item] += 1
t_num = float(len(data_set)) for item in item_count: if (item_count[item] / t_num) >= min_support:
Lk.add(item)
support_data[item] = item_count[item] / t_num return Lkdef generate_L(data_set, k, min_support): """
Generate all frequent itemsets.
Args:
data_set: A list of transactions. Each transaction contains several items.
k: Maximum number of items for all frequent itemsets.
min_support: The minimum support.
Returns:
L: The list of Lk.
support_data: A dictionary. The key is frequent itemset and the value is support. """
support_data = {}
C1 = create_C1(data_set)
L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data)
Lksub1 = L1.copy()
L = []
L.append(Lksub1) for i in range(2, k+1):
Ci = create_Ck(Lksub1, i)
Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data)
Lksub1 = Li.copy()
L.append(Lksub1) return L, support_datadef generate_big_rules(L, support_data, min_conf): """
Generate big rules from frequent itemsets.
Args:
L: The list of Lk.
support_data: A dictionary. The key is frequent itemset and the value is support.
min_conf: Minimal confidence.
Returns:
big_rule_list: A list which contains all big rules. Each big rule is represented
as a 3-tuple. """
big_rule_list = []
sub_set_list = [] for i in range(0, len(L)): for freq_set in L[i]: for sub_set in sub_set_list: if sub_set.issubset(freq_set):
conf = support_data[freq_set] / support_data[freq_set - sub_set]
big_rule = (freq_set - sub_set, sub_set, conf) if conf >= min_conf and big_rule not in big_rule_list: # print freq_set-sub_set, " => ", sub_set, "conf: ", conf big_rule_list.append(big_rule)
sub_set_list.append(freq_set) return big_rule_listif __name__ == "__main__": """
Test """
file_path = "test_aa.xlsx"
data_set,k = local_data(file_path)
L, support_data = generate_L(data_set, k, min_support=0.2)
big_rules_list = generate_big_rules(L, support_data, min_conf=0.4) print(L) for Lk in L: if len(list(Lk)) == 0: break
print("="*50) print("frequent " + str(len(list(Lk)[0])) + "-itemsets\t\tsupport") print("="*50) for freq_set in Lk: print(freq_set, support_data[freq_set]) print() print("Big Rules") for item in big_rules_list: print(item[0], "=>", item[1], "conf: ", item[2])
File format:
test_aa.xlsx
name con
T1 2,3,5T2 1,2,4T3 3,5T5 2,3,4T6 2,3,5T7 1,2,4T8 3,5T9 2,3,4T10 1,2,3,4,5
Related free learning recommendations: python Video tutorial



