
1. Time complexity
Definition: In computer science, the time of an algorithm Complexity is a function that quantitatively describes the running time of the algorithm. Theoretically speaking, the time it takes to execute an algorithm can only be known if you put your program on the machine and run it. However, we have a set of time complexity Analysis method of degree. The time spent by an algorithm is proportional to the number of executions of its statements. The number of executions of the basic operations in the algorithm is the time complexity of the algorithm.2. Time complexity Why not measure it in time instead of the number of times a basic statement is run?
The execution time of the algorithm depends on the specific software and hardware environment. Therefore, the time complexity of the algorithm cannot be measured by the length of execution time, but by the order of magnitude of the number of basic statement executions.3. The O asymptotic notation of time complexity (Big O notation)
is a mathematical symbol used to describe the asymptotic behavior of a function. Big O-order method derivation: Calculate the order of magnitude of the number of executions of a basic statement;
Only need to calculate the order of magnitude of the number of executions of a basic statement, which means that as long as the highest power in the function of the number of executions of a basic statement is guaranteed to be correct, that is Yes, all coefficients of lower powers and higher powers can be ignored. This simplifies algorithm analysis and focuses attention on the most important point: growth rate.
If the algorithm contains nested loops, the basic statement is usually the innermost loop body. If the algorithm contains parallel loops, the time complexity of the parallel loops is added. For example:
for (i=1; i The time complexity of the first for loop is Ο(n), the time complexity of the second for loop is Ο(n2), then the time complexity of the entire algorithm is Ο(n n2)=Ο(n2). <p></p><p> 4. Time complexity: optimal, average, worst case. Why does time complexity look at the worst case? <strong></strong></p> The worst-case complexity is the maximum resource consumed by all possible input data. If the worst-case complexity meets our requirements, we can guarantee that it will work in all cases. There will be no problem. <p></p> Some algorithms often encounter the worst case. For example, a search algorithm often needs to find a value that does not exist. <p> Maybe you think the complexity of the average case is more attractive to you, but there are several problems with the average case. First, it is difficult to calculate. The worst-case complexity of most algorithms is much easier to calculate than the average case. Second, the average-case and worst-case complexity of many algorithms are the same. Third, What is the true average? It is also unreasonable to assume that all possible input data have the same probability. In fact, most situations are different. And the distribution function of the input data is probably something you have no way of knowing. <br>It makes no sense to consider the complexity of the best case scenario. <br></p><p> 5. How to solve: the time complexity of binary search, recursive factorial, and recursive Fibonacci? <strong></strong></p> Binary search: The time complexity of searching through origami is O(logN);<p> Recursive factorial search: Recurse the basic operations N times to get the time complexity of O(N);<br> Recursive Fibonacci: Analysis shows that the basic operation is recursive 2<br>N times, and the time complexity is O(2<sup>N);</sup></p><p> 6. What is space complexity ? <strong></strong></p> Space complexity is a measure of the amount of storage space an algorithm temporarily occupies during operation. Space complexity is not how many bytes of space the program occupies, because this does not make much sense, so the space Complexity is calculated as the number of variables. The calculation rules of space complexity are basically similar to time complexity, and are also expressed using the big O asymptotic method.<p></p><p><strong> 7.如何求空间复杂度? 普通函数&递归函数</strong></p><p style="line-height: 2em;"> 一个算法的空间复杂度只考虑在运行过程中为局部变量分配的存储空间的大小,它包括为参数表中形参变量分配的存储空间和为在函数体中定义的局部变量分配的存储空间两个部分。若一个算法为 递归算法,其空间复杂度为递归所使用的堆栈空间的大小,它等于一次调用所分配的临时存储空间的大小乘以被调用的次数(即为递归调用的次数加1,这个1表示开始进行的一次非递归调用)。算法的空间复杂度一般也以数量级的形式给出。如当一个算法的空间复杂度为一个常量,即不随被处理数据量n的大小而改变时,可表示为O(1);当一个算法的空间复杂度与以2为底的n的对数成正比时,可表示为O(log2n);当一个算法的空间复杂度与n成线性比例关系时,可表示为O(n).若形参为数组,则只需要为它分配一个存储由实参传送来的一个地址指针的空间,即一个机器字长空间;若形参为引用方式,则也只需要为其分配存储一个地址的空间,用它来存储对应实参变量的地址,以便由系统自动引用实参变量。</p><p style="line-height: 2em;"><strong> 8. 分析递归斐波那契数列的:时间、空间复杂度,并对其进行优化,伪递归优化—>循环优化</strong></p><pre class="brush:php;toolbar:false">long long Fib(int N) {
if (N <p> 普通递归实现的斐波那契数列:<br> 时间复杂度:O(2^n)<br><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/article/000/000/051/79601e8681a1e563f3ddfcadebcb758c-0.png?x-oss-process=image/resize,p_40" class="lazy" alt="How to evaluate the quality of an algorithm"><br> 计算并根据<strong>O渐进表示法</strong>得出时间复杂度.</p><p> 空间复杂度:O(N);递归深度乘以(每一次递归的空间占用{有辅助空间或常量})</p><p> 伪递归优化:</p><pre class="brush:php;toolbar:false">long long fib (long long first, longlong second, int N) {
if(N <p> 时间复杂度:<br> O(N);<br> 递归深度乘以每次递归的循环次数<br> 空间复杂度:<br> O(1)或O(N)<br> 关键看编译器是否优化,优化则为O(1)否则O(N);</p><p> 循环优化:</p><pre class="brush:php;toolbar:false">long long Fib(int N) {
long long first = 1;
long long second = 1;
long long ret = 0;
for (int i = 3; i <p> 时间复杂度:O(N);</p><p> 空间复杂度:O(1);</p><p> <strong>9.常见时间复杂度</strong></p><p> 常见的算法时间复杂度由小到大依次为: Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<Ο(n3)<…<Ο(2n)<Ο(n!) Ο(1)表示基本语句的执行次数是一个常数,一般来说,只要算法中不存在循环语句,其时间复杂度就是Ο(1)。Ο(log2n)、Ο(n)、Ο(nlog2n)、Ο(n2)和Ο(n3)称为多项式时间,而Ο(2n)和Ο(n!)称为指数时间。</p><link href="https://csdnimg.cn/release/phoenix/mdeditor/markdown_views-60ecaf1f42.css" rel="stylesheet"><!-- flowchart 箭头图标 勿删 --><svg xmlns="http://www.w3.org/2000/svg" style="display: none;"><path stroke-linecap="round" d="M5,0 0,2.5 5,5z" id="raphael-marker-block" style="-webkit-tap-highlight-color: rgba(0, 0, 0, 0);"></path></svg>The above is the detailed content of How to evaluate the quality of an algorithm. For more information, please follow other related articles on the PHP Chinese website!
 特斯拉自动驾驶算法和模型解读Apr 11, 2023 pm 12:04 PM
特斯拉自动驾驶算法和模型解读Apr 11, 2023 pm 12:04 PM特斯拉是一个典型的AI公司,过去一年训练了75000个神经网络,意味着每8分钟就要出一个新的模型,共有281个模型用到了特斯拉的车上。接下来我们分几个方面来解读特斯拉FSD的算法和模型进展。01 感知 Occupancy Network特斯拉今年在感知方面的一个重点技术是Occupancy Network (占据网络)。研究机器人技术的同学肯定对occupancy grid不会陌生,occupancy表示空间中每个3D体素(voxel)是否被占据,可以是0/1二元表示,也可以是[0, 1]之间的
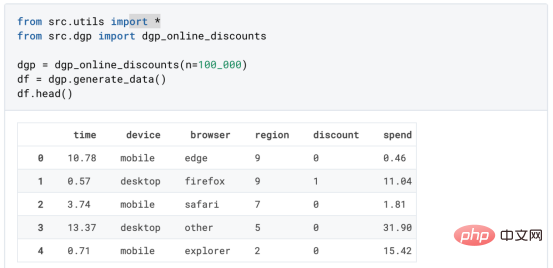 基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM
基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM译者 | 朱先忠审校 | 孙淑娟在我之前的博客中,我们已经了解了如何使用因果树来评估政策的异质处理效应。如果你还没有阅读过,我建议你在阅读本文前先读一遍,因为我们在本文中认为你已经了解了此文中的部分与本文相关的内容。为什么是异质处理效应(HTE:heterogenous treatment effects)呢?首先,对异质处理效应的估计允许我们根据它们的预期结果(疾病、公司收入、客户满意度等)选择提供处理(药物、广告、产品等)的用户(患者、用户、客户等)。换句话说,估计HTE有助于我
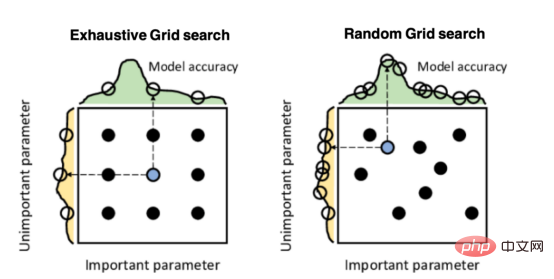 Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM
Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM译者 | 朱先忠审校 | 孙淑娟引言模型超参数(或模型设置)的优化可能是训练机器学习算法中最重要的一步,因为它可以找到最小化模型损失函数的最佳参数。这一步对于构建不易过拟合的泛化模型也是必不可少的。优化模型超参数的最著名技术是穷举网格搜索和随机网格搜索。在第一种方法中,搜索空间被定义为跨越每个模型超参数的域的网格。通过在网格的每个点上训练模型来获得最优超参数。尽管网格搜索非常容易实现,但它在计算上变得昂贵,尤其是当要优化的变量数量很大时。另一方面,随机网格搜索是一种更快的优化方法,可以提供更好的
 因果推断主要技术思想与方法总结Apr 12, 2023 am 08:10 AM
因果推断主要技术思想与方法总结Apr 12, 2023 am 08:10 AM导读:因果推断是数据科学的一个重要分支,在互联网和工业界的产品迭代、算法和激励策略的评估中都扮演者重要的角色,结合数据、实验或者统计计量模型来计算新的改变带来的收益,是决策制定的基础。然而,因果推断并不是一件简单的事情。首先,在日常生活中,人们常常把相关和因果混为一谈。相关往往代表着两个变量具有同时增长或者降低的趋势,但是因果意味着我们想要知道对一个变量施加改变的时候会发生什么样的结果,或者说我们期望得到反事实的结果,如果过去做了不一样的动作,未来是否会发生改变?然而难点在于,反事实的数据往往是
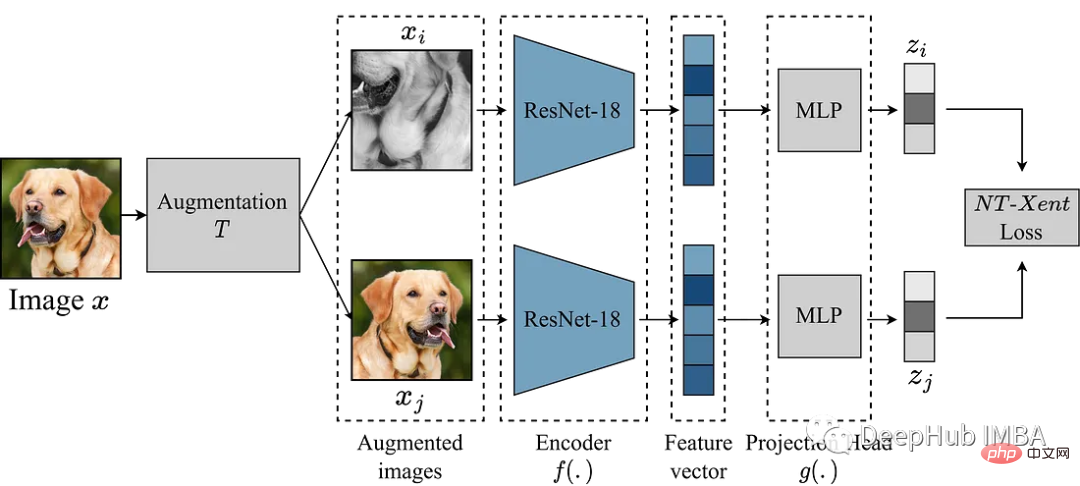 使用Pytorch实现对比学习SimCLR 进行自监督预训练Apr 10, 2023 pm 02:11 PM
使用Pytorch实现对比学习SimCLR 进行自监督预训练Apr 10, 2023 pm 02:11 PMSimCLR(Simple Framework for Contrastive Learning of Representations)是一种学习图像表示的自监督技术。 与传统的监督学习方法不同,SimCLR 不依赖标记数据来学习有用的表示。 它利用对比学习框架来学习一组有用的特征,这些特征可以从未标记的图像中捕获高级语义信息。SimCLR 已被证明在各种图像分类基准上优于最先进的无监督学习方法。 并且它学习到的表示可以很容易地转移到下游任务,例如对象检测、语义分割和小样本学习,只需在较小的标记
 盒马供应链算法实战Apr 10, 2023 pm 09:11 PM
盒马供应链算法实战Apr 10, 2023 pm 09:11 PM一、盒马供应链介绍1、盒马商业模式盒马是一个技术创新的公司,更是一个消费驱动的公司,回归消费者价值:买的到、买的好、买的方便、买的放心、买的开心。盒马包含盒马鲜生、X 会员店、盒马超云、盒马邻里等多种业务模式,其中最核心的商业模式是线上线下一体化,最快 30 分钟到家的 O2O(即盒马鲜生)模式。2、盒马经营品类介绍盒马精选全球品质商品,追求极致新鲜;结合品类特点和消费者购物体验预期,为不同品类选择最为高效的经营模式。盒马生鲜的销售占比达 60%~70%,是最核心的品类,该品类的特点是用户预期时
 人类反超 AI:DeepMind 用 AI 打破矩阵乘法计算速度 50 年记录一周后,数学家再次刷新Apr 11, 2023 pm 01:16 PM
人类反超 AI:DeepMind 用 AI 打破矩阵乘法计算速度 50 年记录一周后,数学家再次刷新Apr 11, 2023 pm 01:16 PM10 月 5 日,AlphaTensor 横空出世,DeepMind 宣布其解决了数学领域 50 年来一个悬而未决的数学算法问题,即矩阵乘法。AlphaTensor 成为首个用于为矩阵乘法等数学问题发现新颖、高效且可证明正确的算法的 AI 系统。论文《Discovering faster matrix multiplication algorithms with reinforcement learning》也登上了 Nature 封面。然而,AlphaTensor 的记录仅保持了一周,便被人类
 研究表明强化学习模型容易受到成员推理攻击Apr 09, 2023 pm 08:01 PM
研究表明强化学习模型容易受到成员推理攻击Apr 09, 2023 pm 08:01 PM译者 | 李睿 审校 | 孙淑娟随着机器学习成为人们每天都在使用的很多应用程序的一部分,人们越来越关注如何识别和解决机器学习模型的安全和隐私方面的威胁。 然而,不同机器学习范式面临的安全威胁各不相同,机器学习安全的某些领域仍未得到充分研究。尤其是强化学习算法的安全性近年来并未受到太多关注。 加拿大的麦吉尔大学、机器学习实验室(MILA)和滑铁卢大学的研究人员开展了一项新研究,主要侧重于深度强化学习算法的隐私威胁。研究人员提出了一个框架,用于测试强化学习模型对成员推理攻击的脆弱性。 研究

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

SublimeText3 Linux new version
SublimeText3 Linux latest version

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

WebStorm Mac version
Useful JavaScript development tools

VSCode Windows 64-bit Download
A free and powerful IDE editor launched by Microsoft






