Home >Common Problem >Depth-first traversal and breadth-first traversal
Depth-first traversal and breadth-first traversal
- (*-*)浩Original
- 2019-12-19 09:29:0216133browse

Depth-first traversal
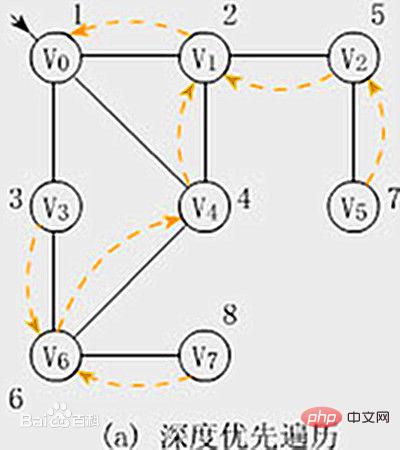
Assume that the initial state of a given graph G is that all vertices have not been visited. Select any vertex v in G as the initial starting point (source point), then the depth-first traversal can be defined as follows: first visit the starting point v and mark it as visited; then start from v to search each adjacent point of v. w. (Recommended learning: web front-end video tutorial)
If w has not been visited before, use w as the new starting point to continue depth-first traversal until all paths in the graph have paths to the source point v Until all connected vertices (also called vertices reachable from the source point) have been visited.
If there are still unvisited vertices in the graph at this time, select another unvisited vertex as a new source point and repeat the above process until all vertices in the graph have been visited.
Depth-first traversal of a graph is similar to pre-order traversal of a tree. The characteristic of the search method adopted is to search in the depth direction first as much as possible. This search method is called depth-first search. Accordingly, traversing the graph using this method is naturally called depth-first traversal of the graph.
To put it bluntly, depth-first traversal is an algorithm that will not hit the wall without hitting the south wall. After completing a path, it will backtrack to the forked node and continue traversing.
As shown in the picture:
Breadth-first traversal
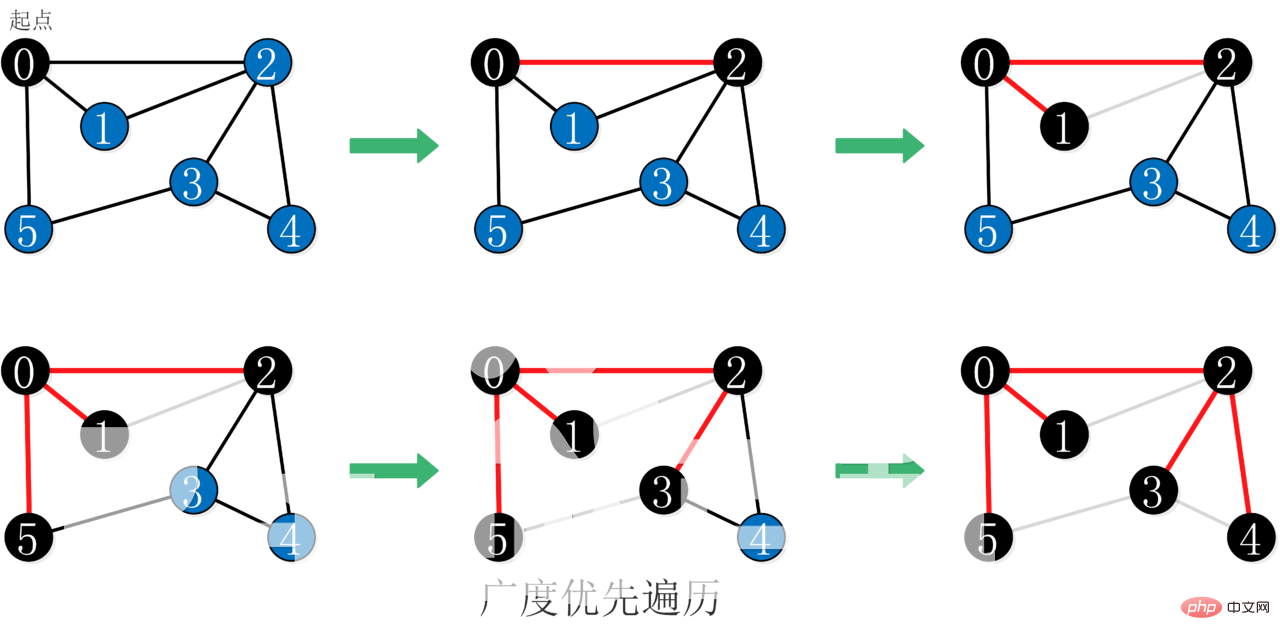
From a certain Start from the vertex V0 and visit this vertex;
Start from V0 and visit each unvisited adjacent point W1, W2,...,Wk of V0; then, start from W1, W2,...,Wk in order to visit each of them Adjacent points that have not been visited;
Repeat step 2 until all vertices are visited.
This is a layer-by-layer progressive algorithm, similar to the layer-order traversal of a tree.
During breadth-first search, it will be traversed from the starting point in a "layer by layer" expansion method. During expansion, every time a point is found, it will be added to the queue until the entire graph has been traversed. Location.
The above is the detailed content of Depth-first traversal and breadth-first traversal. For more information, please follow other related articles on the PHP Chinese website!

