Home >Common Problem >What must a recursive algorithm include?
What must a recursive algorithm include?
- (*-*)浩Original
- 2019-12-11 10:51:0910111browse
Recursion algorithm (English: recursion algorithm) in computer science refers to a method of solving problems by repeatedly decomposing the problem into similar sub-problems.

The recursive method can be used to solve many computer science problems, so it is a very important concept in computer science.
Most programming languages support self-calling of functions. In these languages, functions can perform recursion by calling themselves. (Recommended learning: web front-end video tutorial)
Computing theory can prove that the role of recursion can completely replace loops, so it is customary to use recursion to implement loops in many functional programming languages (such as Scheme) .
Recursive program
In a programming language that supports self-calling, recursion can be completed through a simple function call. For example, a program for calculating factorial can be mathematically defined as:
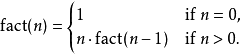
This program can be written in Scheme language:
(define (factorial n) (if (= n 0) 1 (* n (factorial (- n 1)))))<br/>
Fixed point combinator
Even a program If the language does not support self-calling, if the function is a first-class object (that is, it can be created at runtime and treated as a variable), recursion can be generated through a fixed-point combinator.
The following Scheme program does not use self-calling, but uses a fixed-point combinator called Z operator (English: Z combinator), so it can also achieve the purpose of recursion.
(define Z (lambda (f) ((lambda (recur) (f (lambda arg (apply (recur recur) arg)))) (lambda (recur) (f (lambda arg (apply (recur recur) arg)))))))(define fact (Z (lambda (f) (lambda (n) (if (<= n 0) 1 (* n (f (- n 1))))))))<br/>
The above is the detailed content of What must a recursive algorithm include?. For more information, please follow other related articles on the PHP Chinese website!

