 Common Problem
Common Problem The in-order traversal sequence of a certain binary tree is cbade, and the pre-order traversal sequence is
The in-order traversal sequence of a certain binary tree is cbade, and the pre-order traversal sequence isThe in-order traversal sequence of a certain binary tree is cbade, and the pre-order traversal sequence is
The in-order traversal sequence of a certain binary tree is CBADE, the post-order traversal sequence is CBADE, and the pre-order traversal sequence is EDABC.
First of all, post-order traversal means to first visit the left and right child nodes of the parent node, and finally visit the parent node.
Therefore, the last element of the postorder traversal sequence is the root node of the binary tree, which is E, so CBAD is the descendant node of E. (Recommended learning: web front-end video tutorial)
Now continue to look at in-order traversal. In-order traversal means that the left child of the parent node is visited first, then the parent node is visited, and finally Right child.
So the CBAD on the left side of root node E is its left child, and it has no right child. Then go back to the post-order traversal sequence again, because we already know that E is the root node, so we only need to consider CBAD.
So D is the direct left child of E, that is, D is the root node of the left subtree. Then continue to check the in-order traversal, you can find that D has no right subtree, only the left child CBA.
By analogy, it can be found that all nodes of this binary tree have no right children, and they are EDABC from top to bottom, so the preorder traversal is EDABC.
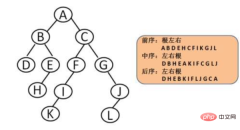
Characteristics of binary trees:
1. Each node has at most two subtrees, so there is no degree greater than 2 node.
2. The left subtree and the right subtree are in order, and the order cannot be reversed arbitrarily.
3. Even if a node in the tree has only one subtree, it must be distinguished whether it is a left subtree or a right subtree.
The above is the detailed content of The in-order traversal sequence of a certain binary tree is cbade, and the pre-order traversal sequence is. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

SublimeText3 English version
Recommended: Win version, supports code prompts!

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.




