
Binary tree has the following five properties:
#1. At the ith (i>=1) of the binary tree A layer has at most 2^(i - 1) nodes.
2. A binary tree with depth k (k>=0) has at least k nodes and at most 2^kk1 nodes.
3. For any non-empty binary tree, if the number of leaf nodes is n0 and the number of non-leaf nodes with degree 2 is n2, then n0 = n2 +1.
4. The depth of a complete binary tree with n nodes is int_UP (log (2, n 1)).
5. If a complete binary tree with n nodes is taken from top to bottom, the nodes in the same layer are numbered 1, 2, 3 continuously from left to right. . . . . . , n, and then store each node in the tree sequentially in a one-dimensional array according to this node number, and call the node numbered i as node i (i>=1 && i
(1) If i = 1, then node i is the root and has no parent node; if i> 1, then the parent node of node i is node int_DOWN (i / 2 );
(2) If 2*i
(3) If 2*i
(4) If the node number i is an odd number, and i! =1, it is in the right sibling position, then its left sibling is node i-1;
(5) If node number i is an even number, and i! =n, it is in the left sibling position, then its right sibling is node i+1;
(6) The level of node i is int_DOWN (log (2, i)) + 1.
Proof of some properties
Property 1 can be proved through mathematical induction
Proof of property 2:
By property 1 It can be seen that the maximum total number of nodes in layer k can be expressed as 2^0+2^ 1+...+2^ (k-1) = 2^k-1;
Proof of Property 3:
First, From the perspective of nodes, n1+n2+n0=n, let this be equation (1);
Looking from the perspective of edges, n2 is connected to two edges, n1 is connected to one edge, and n nodes are connected in pairs. We need n-1 sides, and we can get 2*n2+n1=n-1, which is equation (2);
From equation (1)-(2), we can get
n0 -n2=1.
The above is the detailed content of 5 properties of binary trees. For more information, please follow other related articles on the PHP Chinese website!
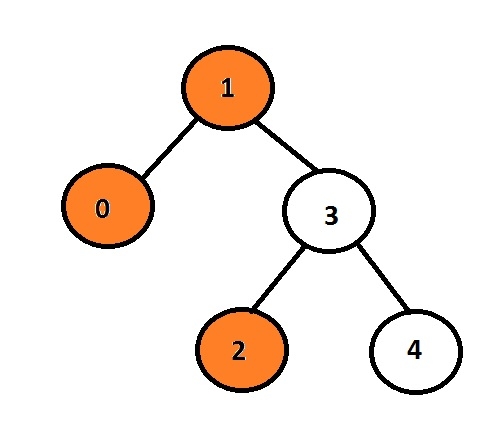 在C语言中打印二叉树的左视图Sep 03, 2023 pm 01:25 PM
在C语言中打印二叉树的左视图Sep 03, 2023 pm 01:25 PM任务是打印给定二叉树的左节点。首先,用户将插入数据,从而生成二叉树,然后打印所形成的树的左视图。每个节点最多可以有2个子节点,因此这里程序必须仅遍历与节点关联的左指针如果左指针不为空,则意味着它将有一些与之关联的数据或指针,否则它将是要打印并显示为输出的左子级。示例Input:10324Output:102这里,橙色节点代表二叉树的左视图。在给定的图中,数据为1的节点是根节点,因此它将被打印,而不是转到左子节点,它将打印0,然后它将转到3并打印其左子节点,即2。我们可以使用递归方法来存储节点的级
 Java中的二叉树结构详解Jun 16, 2023 am 08:58 AM
Java中的二叉树结构详解Jun 16, 2023 am 08:58 AM二叉树是计算机科学中常见的数据结构,也是Java编程中常用的一种数据结构。本文将详细介绍Java中的二叉树结构。一、什么是二叉树?在计算机科学中,二叉树是一种树形结构,每个节点最多有两个子节点。其中,左侧子节点比父节点小,右侧子节点则比父节点大。在Java编程中,常用二叉树表示排序,搜索以及提高对数据的查询效率。二、Java中的二叉树实现在Java中,二叉树
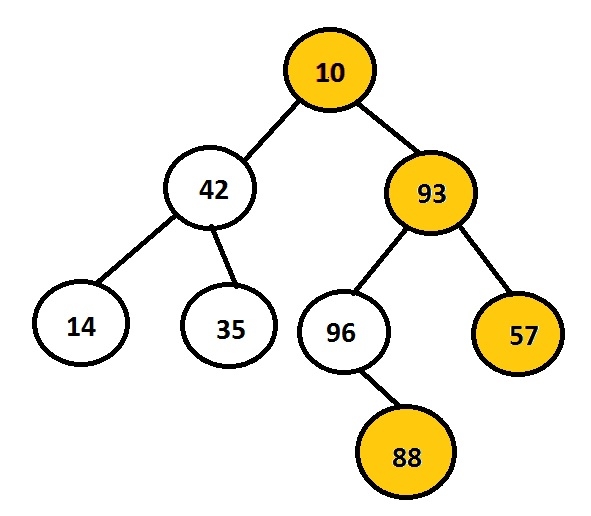 在C语言中,将二叉树的右视图打印出来Sep 16, 2023 pm 11:13 PM
在C语言中,将二叉树的右视图打印出来Sep 16, 2023 pm 11:13 PM任务是打印给定二叉树的右节点。首先用户将插入数据以创建二叉树,然后打印所形成的树的右视图。上图展示了使用节点10、42、93、14、35、96、57和88创建的二叉树,其中选择并显示在树的右侧的节点。例如,10、93、57和88是二叉树的最右节点。示例Input:1042931435965788Output:10935788每个节点都有两个指针,即左指针和右指针。根据这个问题,程序只需遍历右节点。因此,不需要考虑节点的左子节点。右视图存储了所有那些是其所在层级的最后一个节点的节点。因此,我们可以
 如何使用Python实现二叉树的遍历Jun 09, 2023 pm 09:12 PM
如何使用Python实现二叉树的遍历Jun 09, 2023 pm 09:12 PM作为一种常用的数据结构,二叉树经常被用来存储数据、搜索和排序。遍历二叉树是非常常见的操作之一。Python作为一种简单易用的编程语言,有许多方法可以实现二叉树的遍历。本文将介绍如何使用Python实现二叉树的前序、中序和后序遍历。二叉树的基础在学习二叉树的遍历之前,我们需要了解二叉树的基本概念。二叉树由节点组成,每个节点都有一个值和两个子节点(左子节点和右子
 二叉树中等腰三角形的数量Sep 05, 2023 am 09:41 AM
二叉树中等腰三角形的数量Sep 05, 2023 am 09:41 AM二叉树是一种数据结构,其中每个节点最多可以有两个子节点。这些孩子分别称为左孩子和右孩子。假设我们得到了一个父数组表示,您必须使用它来创建一棵二叉树。二叉树可能有几个等腰三角形。我们必须找到该二叉树中可能的等腰三角形的总数。在本文中,我们将探讨几种在C++中解决这个问题的技术。理解问题给你一个父数组。您必须以二叉树的形式表示它,以便数组索引形成树节点的值,而数组中的值给出该特定索引的父节点。请注意,-1始终是根父节点。下面给出的是一个数组及其二叉树表示。Parentarray=[0,-1,3,1,
 Java二叉树实现及具体应用案例详解Jun 15, 2023 pm 11:03 PM
Java二叉树实现及具体应用案例详解Jun 15, 2023 pm 11:03 PMJava二叉树实现及具体应用案例详解二叉树是一种经常在计算机科学中使用的数据结构,可以进行非常高效的查找和排序操作。在本文中,我们将讨论Java中如何实现二叉树及其一些具体应用案例。二叉树的定义二叉树是一种非常重要的数据结构,由根节点(树顶节点)和若干个左子树和右子树组成。每个节点最多有两个子节点,左边的子节点称为左子树,右边的子节点称为右子树。如果节点没有
 PHP实现二叉树的方式与应用Jun 18, 2023 pm 06:28 PM
PHP实现二叉树的方式与应用Jun 18, 2023 pm 06:28 PM在计算机科学中,二叉树是一种重要的数据结构。它由节点和指向它们的边组成,每个节点最多连接两个子节点。二叉树的应用广泛,例如搜索算法、编译器、数据库、内存管理等领域。许多编程语言都支持二叉树数据结构的实现,其中PHP是其中之一。本文将介绍PHP实现二叉树的方式以及其应用。二叉树的定义二叉树是一种数据结构,它由节点和指向它们的边组成。每个节点最多连接两个子节点,
 PHP中的二叉树算法及常见问题解答Jun 09, 2023 am 09:33 AM
PHP中的二叉树算法及常见问题解答Jun 09, 2023 am 09:33 AM随着Web开发的不断发展,PHP作为一种广泛使用的服务器脚本语言,其算法和数据结构也越来越重要。在这些算法和数据结构中,二叉树算法是一个非常重要的概念。本文将介绍PHP中的二叉树算法及其应用,以及常见问题的解答。什么是二叉树?二叉树是一种树形结构,其中每个节点最多有两个子节点,分别为左子节点和右子节点。如果节点没有子节点,则称其为叶子节点。二叉树通常用于搜索

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Safe Exam Browser
Safe Exam Browser is a secure browser environment for taking online exams securely. This software turns any computer into a secure workstation. It controls access to any utility and prevents students from using unauthorized resources.

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool

SublimeText3 Chinese version
Chinese version, very easy to use

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

Dreamweaver CS6
Visual web development tools






