A set of diagrams of data structures to help you understand time complexity

This article uses a set of pictures to let you easily understand what time complexity is. It is interesting and vivid, and has certain learning value. Friends who are interested can come and find out.

The meaning of time complexity

What exactly is time complexity? Let us imagine a scene: One day, Xiao Hui and Da Huang joined a company at the same time...

After one day, Xiao Hui and Da Huang each delivered Code, the functions implemented by the code at both ends are similar. Dahuang's code takes 100 milliseconds to run once and takes up 5MB of memory. Xiao Hui's code takes 100 seconds to run once and takes up 500MB of memory. So...

It can be seen that measuring the quality of code includes two very important indicators:

1. Running time;

2. Space occupied.

Basic operations Number of executions

Regarding the number of executions of basic operations of the code, we use four scenes in life as a metaphor:

Scenario 1 : Give Xiao Hui a 10-inch loaf of bread. Xiao Hui eats 1 inch every 3 days. How many days does it take to eat the entire loaf?

The answer is naturally 3 X 10 = 30 days.

What if the length of the bread is N inches?

It will take 3 X n = 3n days to eat the entire bread at this time.

If you use a function to express this relative time, it can be recorded as T(n) = 3n.

Scenario 2: Give Xiao Hui a 16-inch loaf of bread. Xiao Hui eats half of the remaining length of the bread every 5 days. He eats 8 inches the first time and 8 inches the second time. 4 inches fell off, and 2 inches were eaten for the third time... So how many days will it take for Xiao Hui to eat only 1 inch of bread?

To translate this question, the number 16 is continuously divided by 2. How many times will the result equal 1? This involves logarithms in mathematics. The logarithm of 16 with base 2 can be abbreviated as log16.

Therefore, it takes 5 X log16 = 5 X 4 = 20 days to eat only 1 inch of bread.

What if the length of the bread is N inches?

Requires 5 X logn = 5logn days, recorded as T(n) = 5logn.

Scenario 3: Give Xiao Hui a 10-inch piece of bread and a chicken drumstick. Xiao Hui eats one drumstick every 2 days. So how many days does it take for Xiao Hui to eat the entire chicken leg?

The answer is naturally 2 days. Because it only means eating chicken legs, it has nothing to do with the 10-inch bread.

What if the length of the bread is N inches?

No matter how long the bread is, the time it takes to eat the chicken legs is still 2 days, recorded as T(n) = 2.

Scenario 4: Give Xiao Hui a 10-inch loaf of bread. It will take Xiao Hui 1 day to eat the first inch, 2 days to eat the second inch, and 2 days to eat the third inch. It takes 3 days to eat one inch...for every additional inch, it takes one more day. So how many days does it take for Xiao Hui to eat the entire bread?

The answer is the sum from 1 to 10, which is 55 days.

What if the length of the bread is N inches?

To eat the entire bread at this time, it takes 1 2 3... n-1 n = (1 n)*n/2 = 0.5n^2 0.5n.

Recorded as T(n) = 0.5n^2 0.5n.

What we talked about above is the relative time spent eating. This idea is also applicable to the statistics of the number of basic operations of the program. The four scenarios just now correspond to the four most common execution methods in the program:

Scenario 1: T(n) = 3n, the number of executions is linear.

void eat1(int n){
    for(int i=0; i<n; i++){;
        System.out.println("等待一天");
        System.out.println("等待一天");
        System.out.println("吃一寸面包");
    }
}
vo

Scenario 2: T(n) = 5logn, the number of executions is logarithmic.

void eat2(int n){
   for(int i=1; i<n; i*=2){
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("吃一半面包");
   }
}

Scenario 3: T(n) = 2, the number of executions is constant.

void eat3(int n){
   System.out.println("等待一天");
   System.out.println("吃一个鸡腿");
}

Scenario 4: T(n) = 0.5n^2 0.5n, the number of executions is a polynomial.

void eat4(int n){
   for(int i=0; i<n; i++){
       for(int j=0; j<i; j++){
           System.out.println("等待一天");
       }
       System.out.println("吃一寸面包");
   }
}

Asymptotic time complexity

With the function T(n) of the number of execution times of basic operations, can we analyze and compare the running time of a piece of code? There are still certain difficulties.

For example, the relative time of algorithm A is T(n) = 100n, and the relative time of algorithm B is T(n) = 5n^2. Which of the two has a longer running time? This depends on the value of n.

So, at this time, there is the concept of asymptotic time complexity (asymptotic time complectiy). The official definition is as follows:

If there is a function f(n), such that when n approaches infinity When , the limit value of T(n)/f(n) is a constant not equal to zero, then f(n) is said to be a function of the same order of magnitude as T(n).

Denoted as T(n) = O(f(n)), O(f(n)) is called the asymptotic time complexity of the algorithm, or time complexity for short.

Asymptotic time complexity is represented by capital O, so it is also called big O notation.

How to derive the time complexity? There are several principles:

1. If the running time is of constant magnitude, use a constant 1 to represent it;

2. Only keep the time function The highest-order term;

3. If the highest-order term exists, the coefficient in front of the highest-order term is omitted.

Let us look back at the four scenes just now.

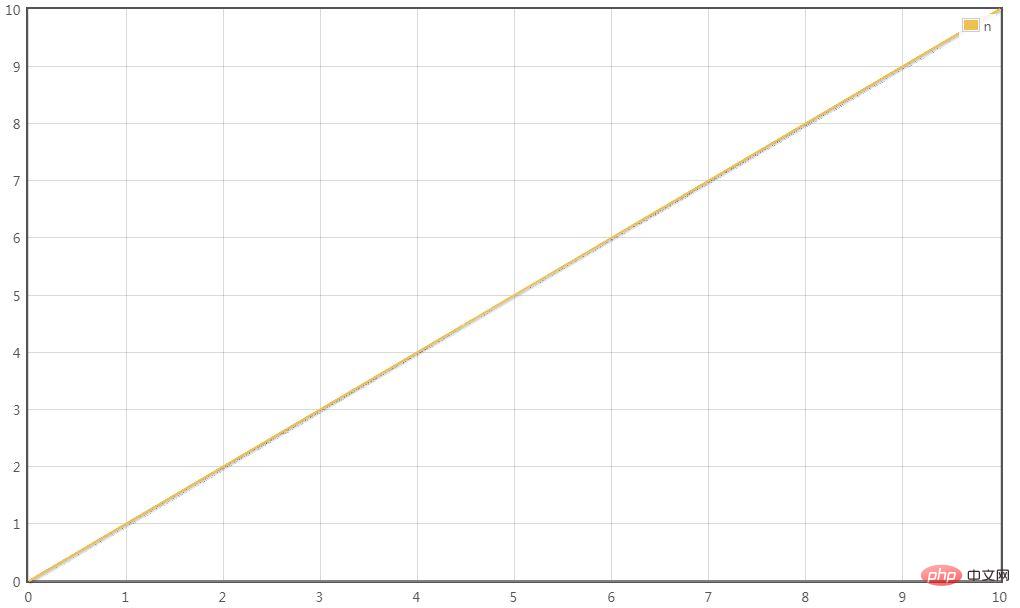
Scenario 1:

T(n) = 3n

The highest order term is 3n, omitting the coefficient 3 and the conversion time The complexity is:

T(n) = O(n)

## Scenario 2:

T (n) = 5logn

The highest order term is 5logn, omitting the coefficient 5, the time complexity of the transformation is:

T(n) = O(logn)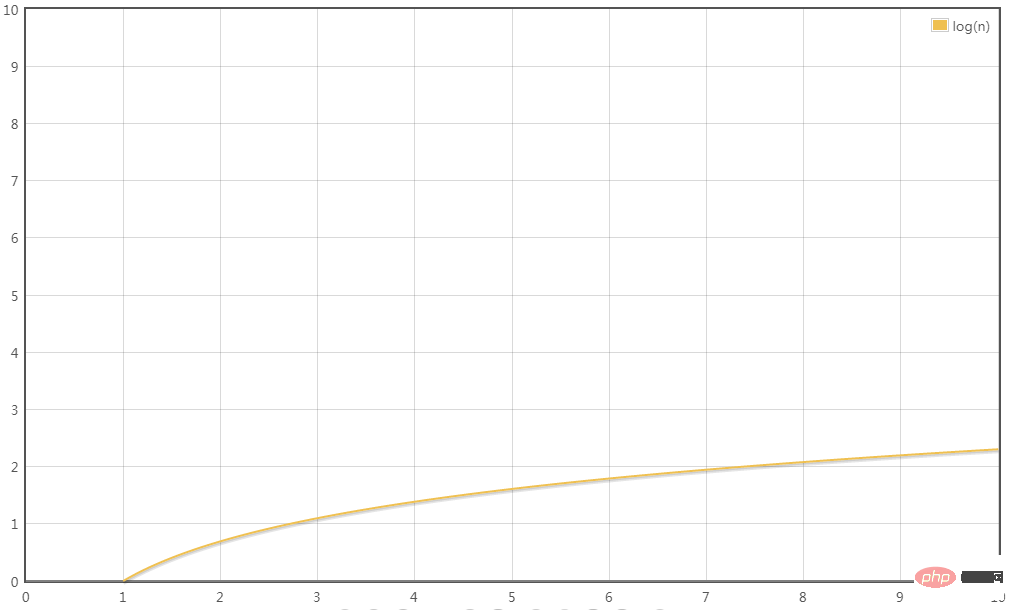

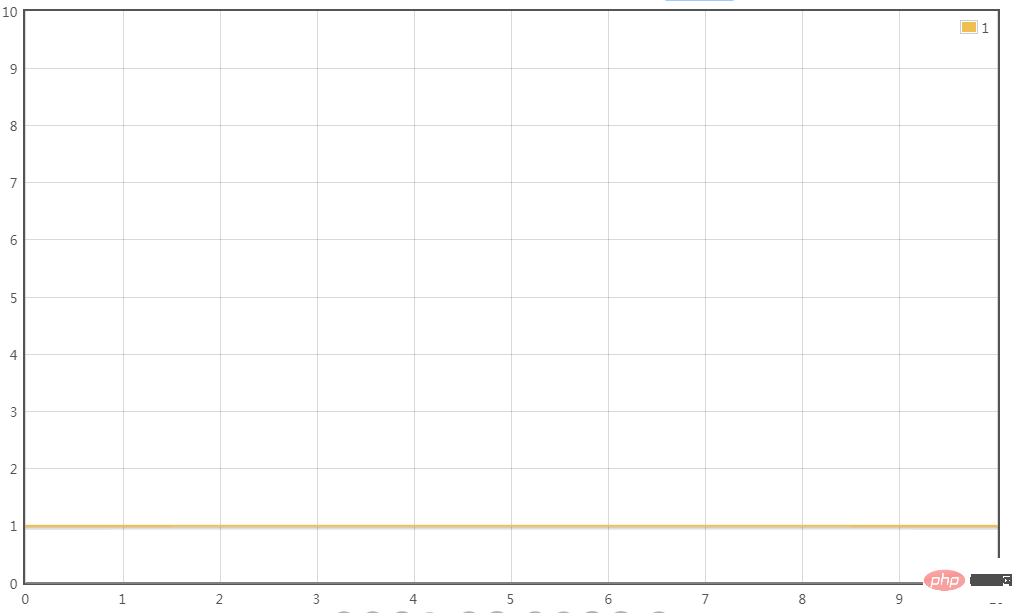
Scenario 3:

T(n) = 2

is only of constant magnitude, and the time complexity of transformation is:

T(n) = O(1)

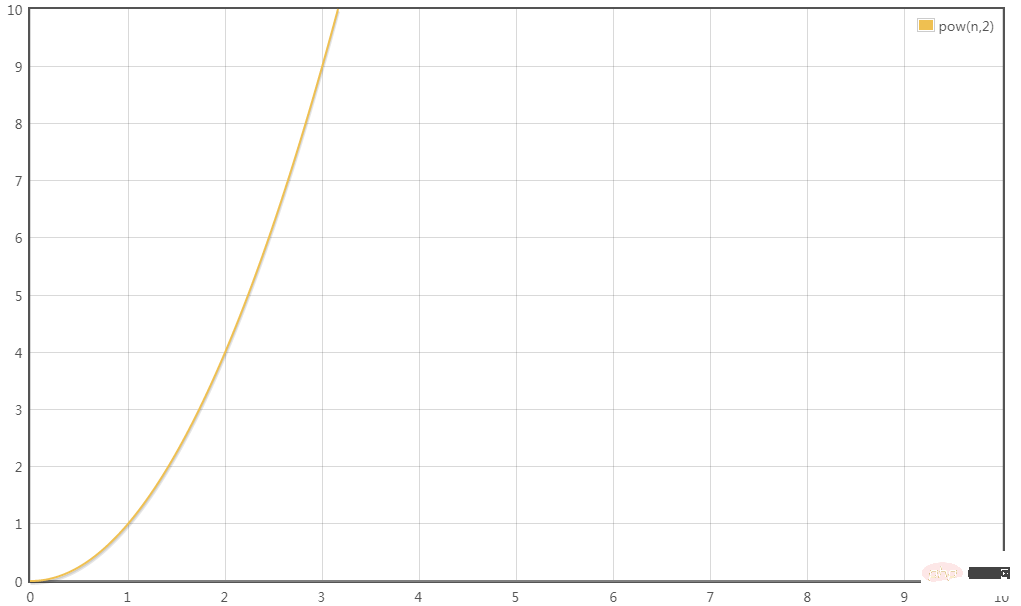
Scenario 4:

T(n) = 0.5n^ 2 0.5n

The highest order term is 0.5n^2, omitting the coefficient 0.5, the time complexity of the transformation is:

T(n) = O(n^2)

Which of these four time complexities takes longer and who saves time? After a little thought, you can come to the conclusion:

O(1)In the world of programming There are various algorithms. In addition to the above four scenarios, there are many different forms of time complexity, such as:

O(nlogn), O(n^3), O(m*n ), O(2^n), O(n!)

In the future, when we travel in the ocean of code, we will continue to encounter algorithms with the above time complexity.

Huge difference in time complexity

Let’s give a chestnut:

The relative time scale of algorithm A is T(n) = 100n, and the time complexity is O(n)

The relative time of algorithm B The scale is T(n) = 5n^2, and the time complexity is O(n^2)

Algorithm A runs on an old computer at Xiao Hui’s home, and algorithm B runs on a certain supercomputer. The running speed is 100 times that of old computers.

So, as the input size n increases, which of the two algorithms runs faster?

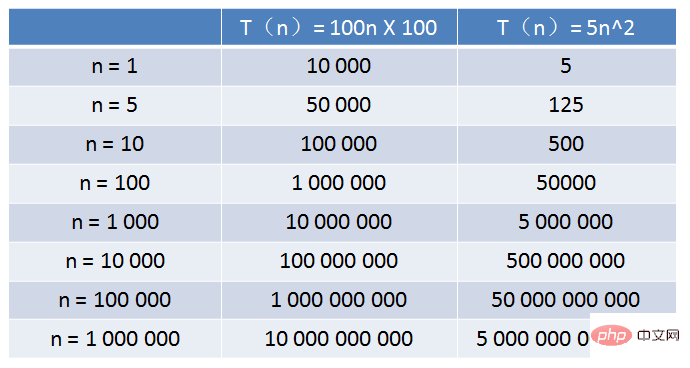
It can be seen from the table that when the value of n is very small, the running time of algorithm A is much longer than that of algorithm B; when the value of n reaches about 1000, The running times of Algorithm A and Algorithm B are close; when the value of n becomes larger and larger, reaching one hundred thousand or one million, the advantages of Algorithm A begin to appear, while Algorithm B becomes slower and slower, and the gap becomes more and more obvious.

This is the difference caused by different time complexities.

If you want to know more technical tutorials, please be sure to pay attention to PHP Chinese website!

The above is the detailed content of A set of diagrams of data structures to help you understand time complexity. For more information, please follow other related articles on the PHP Chinese website!