Home >Java >javaTutorial >Code example of Java implementation of radix sort (RadixSort)
Code example of Java implementation of radix sort (RadixSort)
- 不言forward
- 2019-01-31 11:31:054235browse
This article brings you code examples about Java implementation of radix sorting (RadixSort). It has certain reference value. Friends in need can refer to it. I hope it will be helpful to you.
Radix sorting is a derivative of bucket sorting and counting sorting, because one of these two types is used in radix sorting.
The elements to be sorted by radix sorting must be divided into high and low positions. For example, the words adobe, activiti, and activiti are higher than adobe. This is based on the ascll code.
Now we can ask a question, how to sort the words in the dictionary?
For example, we now have the following words:
"Java", "Mongodb", "Redis", "Kafka", "javascript", "mysql", "mybatis", "kindle", "rpc", "Algorithm", "mergeSort", "quickSort", "Adobe"
How do we sort it? Here we can use radix sorting. The principle of radix sorting is that we divide an element into high and low bits. A single individual, such as Adobe, is divided into A, d, o, b, e, Algorithm is divided into A, l, g, o, r, i, t, h, m, and then we compare it in sequence from right to left, that is Can. But Adobe and Algorithm cannot be directly compared here because they are different in length, so before comparison we should find the length of the longest element, and then complete the remaining short elements to the same length:
Adobe0000
Algorithm
In this way, comparison can be formed, from right to left, 0:m,0:h,0:t,0:i,e:r,b:o,o: g,d:l,A:A, we can compare Adobe > Algorihtm
The principle will be clearer following the following pictures:
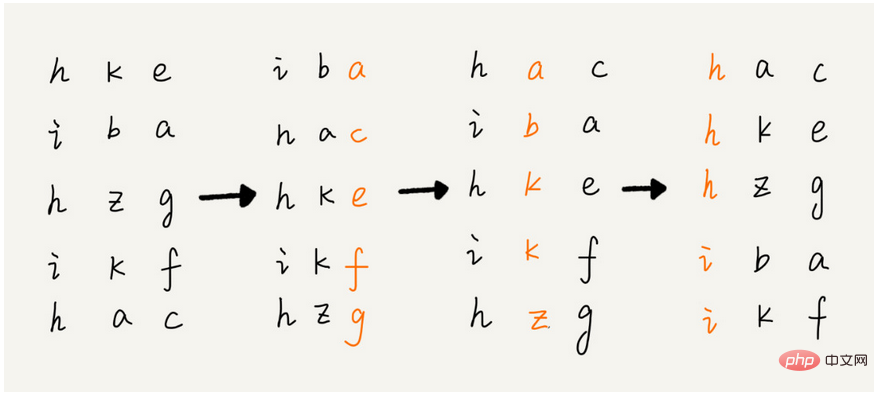
From We can see from the above figure that radix sorting will be compared from right to left (that is, it needs to be traversed many times in our program implementation), and the specific number of traversals depends on how long the longest element is, from right to left To compare elements of each bit on the left, bucket sorting or counting sorting can be used. The time complexity of bucket sorting and counting sorting is O(n). Assuming that the maximum element length is K, the time complexity of radix sorting is O(n). (k * n), and k is generally not very large and can be regarded as a constant, so the time complexity of radix sorting is also O(n).
The following is my Java implementation:
package com.structure.sort;
/**
* @author zhangxingrui
* @create 2019-01-30 14:58
**/
public class RadixSort {
public static void main(String[] args) {
/*int[] numbers = {19, 36, 24, 10, 9, 29, 1, 0, 3, 60, 100, 1001, 999, 520, 123, 96};
radixSort(numbers);
for (int number : numbers) {
System.out.println(number);
}*/
String[] words = {"Java", "Mongodb", "Redis", "Kafka", "javascript", "mysql", "mybatis", "kindle", "rpc", "Algorithm", "mergeSort", "quickSort", "Adobe"};
// String[] words = {"Java", "mongodb", "Kafka"};
radixSort(words);
for (String word : words) {
System.out.println(word.replaceAll("0", ""));
}
}
/**
* @Author: xingrui
* @Description: 基数排序(单词)
* @Date: 15:53 2019/1/30
*/
private static void radixSort(String[] words){
int exp = 0;
int maxLength = getMaxLength(words);
autoComplete(words, maxLength);
for(exp = 1; exp <= maxLength; exp++){
countingSort(words, exp);
}
}
/**
* @Author: xingrui
* @Description: 计数排序(单词)
* @Date: 13:57 2019/1/30
*/
private static void countingSort(String[] words, int exp){
int n = words.length;
String[] r = new String[n];
int[] c = new int[122];
for(int i = 0; i < n; ++i){
int asc = (byte)words[i].charAt(words[i].length() - exp);
c[asc]++;
}
for(int i = 1; i < 122; ++i){
c[i] = c[i-1] + c[i];
}
for (int i = n - 1; i >= 0; --i){
int asc = (byte)words[i].charAt(words[i].length() - exp);
int index = c[asc];
r[index - 1] = words[i];
c[asc]--;
}
for(int i = 0; i < n; ++i){
words[i] = r[i];
}
}
/**
* @Author: xingrui
* @Description: 基数排序(纯数字)
* @Date: 15:00 2019/1/30
*/
private static void radixSort(int[] numbers){
int exp = 0;
int maxNumber = getMaxNumber(numbers);
for(exp = 1; maxNumber/exp > 0; exp *= 10){
countingSort(numbers, exp);
}
}
/**
* @Author: xingrui
* @Description: 计数排序(纯数字)
* @Date: 13:57 2019/1/30
*/
private static void countingSort(int[] numbers, int exp){
int n = numbers.length;
int[] r = new int[n];
int[] c = new int[10];
for(int i = 0; i < n; ++i){
c[numbers[i]/exp % 10]++;
}
for(int i = 1; i < 10; ++i){
c[i] = c[i-1] + c[i];
}
for (int i = n - 1; i >= 0; --i){
int index = c[numbers[i] / exp % 10];
r[index - 1] = numbers[i];
c[numbers[i] / exp % 10]--;
}
for(int i = 0; i < n; ++i){
numbers[i] = r[i];
}
}
/**
* @Author: xingrui
* @Description: 自动补全单词
* @Date: 16:38 2019/1/30
*/
private static void autoComplete(String[] words, int maxLength){
int i = 0;
for (String word : words) {
if(word.length() < maxLength){
int value = maxLength - word.length();
StringBuilder sb = new StringBuilder();
for(int j = 0; j < value; ++j){
sb.append("0");
}
words[i] = word + sb;
}
i++;
}
}
/**
* @Author: xingrui
* @Description: 获取字符串最大的长度
* @Date: 15:56 2019/1/30
*/
private static int getMaxLength(String[] words){
int maxLength = words[0].length();
for(int i = 1; i < words.length; ++i){
if(words[i].length() > maxLength)
maxLength = words[i].length();
}
return maxLength;
}
/**
* @Author: xingrui
* @Description: 获取最大的数字
* @Date: 15:56 2019/1/30
*/
private static int getMaxNumber(int[] numbers){
int maxNumber = numbers[0];
for(int i = 1; i < numbers.length; ++i){
if(numbers[i] > maxNumber)
maxNumber = numbers[i];
}
return maxNumber;
}
}It should be noted that before sorting, you need to find the maximum element length to determine the number of loops and complete shorter elements based on the maximum element length.
Program execution result:

The above is the detailed content of Code example of Java implementation of radix sort (RadixSort). For more information, please follow other related articles on the PHP Chinese website!

