The content of this article is about the code analysis of decimal precision in PHP. It has certain reference value. Friends in need can refer to it. I hope it will be helpful to you.
Encountered precision issues when rounding to two decimal places in the project:
$num = 0.99; $num1 = round($num, 2);//0.98999999999999999 $num2 = floatval($num);//0.98999999999999999
Current solution:
sprintf("%.2f", round($money, 2));//会自动四舍五入
echo substr(sprintf("%.3f",$n), 0, -1);//不四舍五入Test results:
var_dump(json_encode(round(0.99 ,2)));//0.98999999999999999 var_dump(round(0.99 ,2));//0.99 $f = 0.58; var_dump(intval($f * 100));//57
About equal to 57 We can analyze the problem:
Representation of floating point numbers (IEEE 754: IEEE Binary Floating Point Arithmetic Standard):
Floating point numbers, taking 64-bit length (double precision) as an example , will be represented by 1 sign bit (E), 11 exponent bits (Q), and 52 mantissas (M) (a total of 64 bits).
Sign bit: The highest bit indicates the sign of the data, 0 indicates Positive number, 1 means negative number.
Exponent bit: represents the power of the data with base 2, the exponent is represented by offset code
Mantissa: represents the valid digits after the decimal point of the data.
0.58 For binary representation For example, it is an infinitely long value:
The binary representation of 0.58 is basically (52 bits): 0010100011110101110000101000111101011100001010001111
The binary representation of 0.57 (52 bits) is basically: 001000 111101011100001010001111010111000010100011110
The binary numbers of the two, if calculated only through these 52 bits, are:
0.58 --> 0.5799999999999996
0.57 --> 0.5699999999999999
So, the result of 0.58 * 100 will be: 57.999999999, converted to integer type: 57
Regarding the binary representation of floating point numbers, you can refer to: Binary representation of floating point numbers
Similar to:
(0.1 + 0.7) == 0.8//false floor((0.1+0.7)*10)//7 //内部结果可能是:7.9999999999 //所以:不可能精确的用有限位数表达某些十进制分数 1/3=3.33333333333 //而3.333333333333333*3,却不是1
So conclusion:
So never believe that the floating point number result is accurate to the last digit, and never compare whether two floating point numbers are equal. If you really need higher precision, you should use arbitrary precision mathematical functions or gmp functions
It is recommended to use high-precision functions:
High-precision functions
-
bcadd — Addition of 2 arbitrary-precision numbers
-
bccomp — Compare two arbitrary-precision numbers
bcp — Calculate the division of two arbitrary-precision numbers
bcmod — Modulo an arbitrary-precision number
-
bcmul — Multiplication calculation of 2 arbitrary precision numbers
-
bcpow — Power of an arbitrary precision number
- ##bcpowmod — Raise an arbitrary precision number to another, reduced by a specified modulus
- bcscale — Set the default number of decimal places for all bc math functions
- bcsqrt — The square root of an arbitrary-precision number
- bcsub — The subtraction of two arbitrary-precision numbers
function getBcRound($number, $precision = 0)
{
$precision = ($precision < 0)
? 0
: (int) $precision;
if (strcmp(bcadd($number, '0', $precision), bcadd($number, '0', $precision+1)) == 0) {
return bcadd($number, '0', $precision);
}
if (getBcPresion($number) - $precision > 1) {
$number = getBcRound($number, $precision + 1);
}
$t = '0.' . str_repeat('0', $precision) . '5';
return $number < 0
? bcsub($number, $t, $precision)
: bcadd($number, $t, $precision);
}
function getBcPresion($number) {
$dotPosition = strpos($number, '.');
if ($dotPosition === false) {
return 0;
}
return strlen($number) - strpos($number, '.') - 1;
}
$money = getBcRound(0.99, 2); Recommended related articles:
Parsing of AES encrypted files in PHP (with code)
Request codes for post mode and get mode in curl of php
About content analysis of PHP intermediate keys
The above is the detailed content of Code analysis of decimal precision in php. For more information, please follow other related articles on the PHP Chinese website!
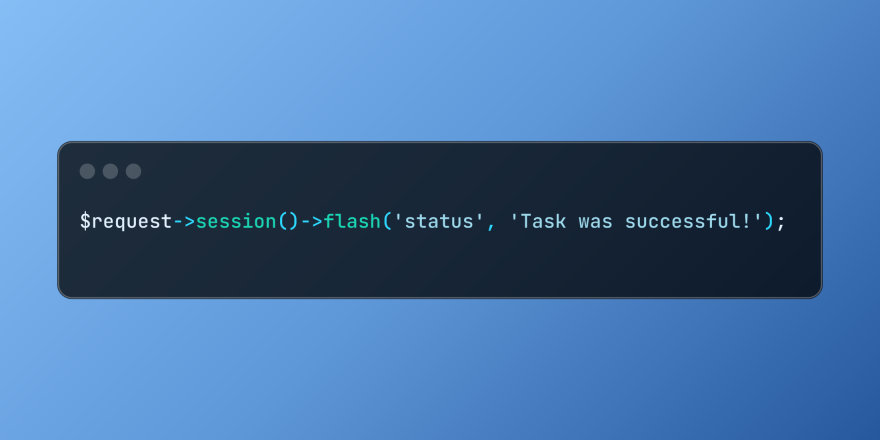 Working with Flash Session Data in LaravelMar 12, 2025 pm 05:08 PM
Working with Flash Session Data in LaravelMar 12, 2025 pm 05:08 PMLaravel simplifies handling temporary session data using its intuitive flash methods. This is perfect for displaying brief messages, alerts, or notifications within your application. Data persists only for the subsequent request by default: $request-
 cURL in PHP: How to Use the PHP cURL Extension in REST APIsMar 14, 2025 am 11:42 AM
cURL in PHP: How to Use the PHP cURL Extension in REST APIsMar 14, 2025 am 11:42 AMThe PHP Client URL (cURL) extension is a powerful tool for developers, enabling seamless interaction with remote servers and REST APIs. By leveraging libcurl, a well-respected multi-protocol file transfer library, PHP cURL facilitates efficient execution of various network protocols, including HTTP, HTTPS, and FTP. This extension offers granular control over HTTP requests, supports multiple concurrent operations, and provides built-in security features.
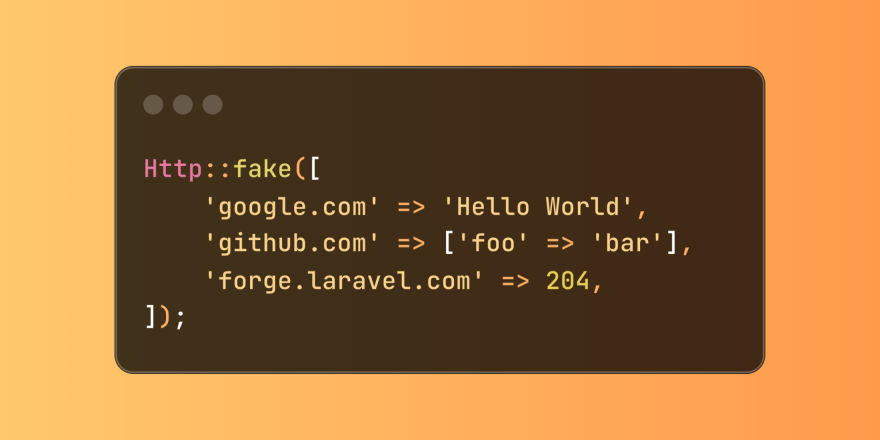 Simplified HTTP Response Mocking in Laravel TestsMar 12, 2025 pm 05:09 PM
Simplified HTTP Response Mocking in Laravel TestsMar 12, 2025 pm 05:09 PMLaravel provides concise HTTP response simulation syntax, simplifying HTTP interaction testing. This approach significantly reduces code redundancy while making your test simulation more intuitive. The basic implementation provides a variety of response type shortcuts: use Illuminate\Support\Facades\Http; Http::fake([ 'google.com' => 'Hello World', 'github.com' => ['foo' => 'bar'], 'forge.laravel.com' =>
 12 Best PHP Chat Scripts on CodeCanyonMar 13, 2025 pm 12:08 PM
12 Best PHP Chat Scripts on CodeCanyonMar 13, 2025 pm 12:08 PMDo you want to provide real-time, instant solutions to your customers' most pressing problems? Live chat lets you have real-time conversations with customers and resolve their problems instantly. It allows you to provide faster service to your custom
 How to Register and Use Laravel Service ProvidersMar 07, 2025 am 01:18 AM
How to Register and Use Laravel Service ProvidersMar 07, 2025 am 01:18 AMLaravel's service container and service providers are fundamental to its architecture. This article explores service containers, details service provider creation, registration, and demonstrates practical usage with examples. We'll begin with an ove
 Explain the concept of late static binding in PHP.Mar 21, 2025 pm 01:33 PM
Explain the concept of late static binding in PHP.Mar 21, 2025 pm 01:33 PMArticle discusses late static binding (LSB) in PHP, introduced in PHP 5.3, allowing runtime resolution of static method calls for more flexible inheritance.Main issue: LSB vs. traditional polymorphism; LSB's practical applications and potential perfo
 PHP Logging: Best Practices for PHP Log AnalysisMar 10, 2025 pm 02:32 PM
PHP Logging: Best Practices for PHP Log AnalysisMar 10, 2025 pm 02:32 PMPHP logging is essential for monitoring and debugging web applications, as well as capturing critical events, errors, and runtime behavior. It provides valuable insights into system performance, helps identify issues, and supports faster troubleshoot
 Customizing/Extending Frameworks: How to add custom functionality.Mar 28, 2025 pm 05:12 PM
Customizing/Extending Frameworks: How to add custom functionality.Mar 28, 2025 pm 05:12 PMThe article discusses adding custom functionality to frameworks, focusing on understanding architecture, identifying extension points, and best practices for integration and debugging.


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

WebStorm Mac version
Useful JavaScript development tools

Notepad++7.3.1
Easy-to-use and free code editor

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.





