 Java
Java javaTutorial
javaTutorial Java source code Integer.bitCount algorithm prototype and process analysis (with code)
Java source code Integer.bitCount algorithm prototype and process analysis (with code)Algorithm: Count the number of bits in the binary expression of the integer that are 1 (Hamming weight). Ordinary algorithm: This should be the first algorithm that comes to mind. Starting from the lowest bit, count whether is 1, the time complexity is O(n), and n is the total number of bits. Optimization algorithm: This algorithm seems confusing at first, but if you think about it carefully, you can find the principle: after n-1, the lowest bit 1 of n is eliminated, and then ANDed with n bits, n becomes the lowest bit 1 and is set to 0 The new integer after.
Ordinary algorithm
public int bitCount(int num) {
int count = 0;
do {
if ((num & 1) == 1) {
count++;
}
num>>=1;
} while (num > 0);
return count;
} should be the first algorithm that comes to mind. Starting from the lowest bit, counting whether it is 1 one by one, the time complexity is O(n) , n is the total number of bits.
Optimization Algorithm
public int countBit2(int num) {
int count = 0;
while (num > 0) {
num = num & (num - 1);
count++;
}
return count;
}This algorithm seems confusing at first glance, but if you think about it carefully, you can find the principle: After n-1, the lowest bit of n is 1 Eliminated, and then ANDed with n bits, n becomes a new integer after the lowest bit 1 is set to 0, such as:
0b101100 减一 0b101011 最低位的1消除,0b101100 & 0b101011 = 0b101000
There will be as many 1s as many times as you can through this cycle, and the time complexity is also O (n), but this n represents the number of bits that are 1, which is generally better than the previous one.
When we think this is already the optimal algorithm, it is not the case
Integer.bitCount
public static int bitCount(int i) {
// HD, Figure 5-2
i = i - ((i >>> 1) & 0x55555555);
i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
i = (i + (i >>> 4)) & 0x0f0f0f0f;
i = i + (i >>> 8);
i = i + (i >>> 16);
return i & 0x3f;
}Finally, in fact, Java's Integer class has provided a method to count bits Bit (unsigned right shift, negative numbers can be counted), at first glance, WTF?
Principle: Imagine that when a column of 1 is placed in front of our human brain, how will we count? Number by number, the principle of the first algorithm. Or counting two by two? This is how this method is implemented. As shown below:
二进制 十进制
1 0 1 1 1 1 1 1 1 1 10 11 11 11 11
01 10 10 10 10 1 2 2 2 2
\ / \ / \/ \/
01 0100 0100 1 4 4
\ / \ /
01 1000 1 8
\ / \ /
1001 9
767的二进制中的1的位数计算过程Each two bits are a group, count the number of 1's respectively, and then store the result in these two bits, such as: 11There are 2 1's , the result is 10, 10 replaces 11 and is stored in the original location. Then perform addition calculations and add up all the results. During the addition process, you can add two by two to reduce the calculation process.
Two bits calculate the number of 1: 0b11: 0b01 0b01 = 0b10 = 2, 0b10: 0b01 0b00 = 0b01 = 1, so it’s clear.
The algorithm is implemented as follows:
First, the left bit of integer i is erased:
i & 0x55555555, and then the offset is added.(i >>> 1) & 0x55555555means: move the left bit to the right, and then erase the left bit, so that the number of 1's in the two bits can be calculated:0b1011=>0b0001 0b0101 = 0b0110There is one 1 in the left two digits and two 1s in the right two digits.At this time, the statistical results of each two digits are stored in
i, which can be added in pairs and finally summed.
Process:
0x55555555 0b01010101010101010101010101010101 0x33333333 0b00110011001100110011001100110011 0x0f0f0f0f 0b00001111000011110000111100001111 0x00ff00ff 0b00000000111111110000000011111111 0x0000ffff 0b00000000000000001111111111111111 0x3f 0b00111111 0b11 11 11 11 11 (i & 0x55555555) + ((i >>> 1) & 0x55555555) = 0b0101010101 + 0b0101010101 = 0b1010101010 0b10 10 10 10 10 (i & 0x33333333) + ((i >>> 2) & 0x33333333) = 0b1000100010 + 0b00100010 = 0b1001000100 0b10 01 00 01 00 (i & 0x0f0f0f0f) + ((i >>> 4) & 0x0f0f0f0f) = 0b1000000100 + 0b0100 = 0b1000001000 0b10 00 00 10 00 (i & 0x00ff00ff) + ((i >>> 8) & 0x00ff00ff) = 0b1000 + 0b10 = 0b1010 0b00 00 00 10 10 (i & 0x0000ffff) + ((i >>> 16) & 0x0000ffff) = 0b1010 + 0 = 0b1010 dec 10
Algorithm prototype:
public static int bitCount(int i) {
i = (i & 0x55555555) + ((i >>> 1) & 0x55555555);
i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
i = (i & 0x0f0f0f0f) + ((i >>> 4) & 0x0f0f0f0f);
i = (i & 0x00ff00ff) + ((i >>> 8) & 0x00ff00ff);
i = (i & 0x0000ffff) + ((i >>> 16) & 0x0000ffff);
return i;
}Time complexity O(1), ok, very ok! But when writing an article, you need to polish it, let alone the algorithm, and then the optimized implementation is implemented in Integer.
Optimization:
Step 1: Calculate the number of 1’s with two bits:
0b11: 0b01 0b01 = 0b10 = 2,0b10: 0b00 0b01 = 0b01 = 1. The research found that:2=0b11-0b1,1=0b10-0b1, can be reduced once to calculate:i = i - ((i >>> 1 ) & 0x55555555)The second step: There is currently no good optimization method
The third step: Actually calculate each The number of 1's in byte is up to 8 (0b1000), accounting for 4 bits. You can finally perform bitwise AND operation to eliminate bits, reducing one
&operation:i = (i (i >> > 4)) & 0x0f0f0f0fSteps 4 and 5: For the same reason as above, you can eliminate the position at the end. However, since int has at most 32 (0b100000) 1s, there is no need to erase the bits in these two steps. The last step is to erase the unnecessary bits:
i & 0x3f
Enlightenment: Great simplicity, a seemingly complex algorithm, but its implementation principle is the simple thinking logic of our brain
7 0b111 i = 7 - ((7>>>1) & 0x55555555) = 6 = 0b110 i = (6 & 0x33333333) + ((6 >>> 2) & 0x33333333) = 2 + 1 = 3 = 0b11 i = (3 + (i >>> 4)) & 0x0f0f0f0f = 3 & 0x0f0f0f0f = 3 = 0b11 i = 3 + (3 >>> 8) = 3 = 0b11 i = 3 + (3 >>> 16) = 3 = 0b11 i = 3 & 0x3f = 3
Related articles:
Detailed explanation Java Reference source code analysis code
java source code analysis Arrays.asList method detailed explanation
Related videos:
Comprehensive analysis of Java annotations
The above is the detailed content of Java source code Integer.bitCount algorithm prototype and process analysis (with code). For more information, please follow other related articles on the PHP Chinese website!
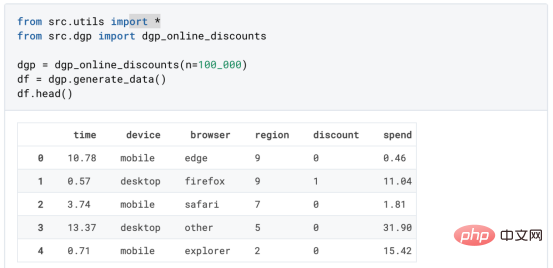 基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM
基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM译者 | 朱先忠审校 | 孙淑娟在我之前的博客中,我们已经了解了如何使用因果树来评估政策的异质处理效应。如果你还没有阅读过,我建议你在阅读本文前先读一遍,因为我们在本文中认为你已经了解了此文中的部分与本文相关的内容。为什么是异质处理效应(HTE:heterogenous treatment effects)呢?首先,对异质处理效应的估计允许我们根据它们的预期结果(疾病、公司收入、客户满意度等)选择提供处理(药物、广告、产品等)的用户(患者、用户、客户等)。换句话说,估计HTE有助于我
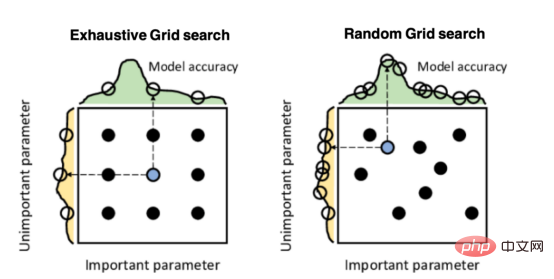 Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM
Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM译者 | 朱先忠审校 | 孙淑娟引言模型超参数(或模型设置)的优化可能是训练机器学习算法中最重要的一步,因为它可以找到最小化模型损失函数的最佳参数。这一步对于构建不易过拟合的泛化模型也是必不可少的。优化模型超参数的最著名技术是穷举网格搜索和随机网格搜索。在第一种方法中,搜索空间被定义为跨越每个模型超参数的域的网格。通过在网格的每个点上训练模型来获得最优超参数。尽管网格搜索非常容易实现,但它在计算上变得昂贵,尤其是当要优化的变量数量很大时。另一方面,随机网格搜索是一种更快的优化方法,可以提供更好的
 二进制算法怎么算Jan 19, 2024 pm 04:38 PM
二进制算法怎么算Jan 19, 2024 pm 04:38 PM二进制算法是一种基于二进制数的运算方法,其基本运算包括加法、减法、乘法和除法。除了基本运算外,二进制算法还包括逻辑运算、位移运算等操作。逻辑运算包括与、或、非等操作,位移运算包括左移和右移操作。这些操作都有对应的规则和操作数的要求。
 如何使用C语言将二进制转换为十六进制?Sep 01, 2023 pm 06:57 PM
如何使用C语言将二进制转换为十六进制?Sep 01, 2023 pm 06:57 PM二进制数以1和0表示。16位的十六进制数系统为{0,1,2,3…..9,A(10),B(11),……F(15)}为了从二进制表示转换为十六进制表示,位串id被分组为4位块,从最低有效侧开始称为半字节。每个块都替换为相应的十六进制数字。让我们看一个示例,以清楚地了解十六进制和二进制数字表示。001111100101101100011101 3 E 5 B&nb
 EDVAC有哪两个重大的改进Mar 02, 2023 pm 02:58 PM
EDVAC有哪两个重大的改进Mar 02, 2023 pm 02:58 PMEDVAC的两个重大的改进:一是采用二进制,二是完成了存贮程序,可以自动地从一个程序指令进到下一个程序指令,其作业可以通过指令自动完成。“指令”包括数据和程序,把它们用码的形式输入到机器的记忆装置中,即用记忆数据的同一记忆装置存贮执行运算的命令,这就是所谓存贮程序的新概念。
 Golang如何读取二进制文件?Mar 21, 2024 am 08:27 AM
Golang如何读取二进制文件?Mar 21, 2024 am 08:27 AMGolang如何读取二进制文件?二进制文件是以二进制形式存储的文件,其中包含了计算机能够识别和处理的数据。在Golang中,我们可以使用一些方法来读取二进制文件,并将其解析成我们想要的数据格式。下面将介绍如何在Golang中读取二进制文件,并给出具体的代码示例。首先,我们需要使用os包中的Open函数打开一个二进制文件,这将返回一个文件对象。然后,我们可以使
 轻松学会Go语言中16进制转二进制Mar 15, 2024 pm 04:45 PM
轻松学会Go语言中16进制转二进制Mar 15, 2024 pm 04:45 PM题目:轻松学会Go语言中16进制转二进制,需要具体代码示例在计算机编程中,经常会涉及到对不同进制数之间的转换操作。其中,16进制和二进制之间的转换是比较常见的。在Go语言中,我们可以通过一些简单的代码示例来实现16进制到二进制的转换,让我们一起来学习一下。首先,我们来了解一下16进制和二进制的表示方法。16进制是一种表示数字的方法,使用0-9和A-F来表示1
 Golang能否处理二进制文件?Mar 20, 2024 pm 04:36 PM
Golang能否处理二进制文件?Mar 20, 2024 pm 04:36 PMGolang能否处理二进制文件?在Go语言中,处理二进制文件是非常常见且方便的。通过使用内置的包和方法,我们可以轻松地读取、写入和操作二进制文件。本文将介绍如何在Go中处理二进制文件,并提供具体的代码示例。读取二进制文件要读取一个二进制文件,我们首先需要打开这个文件并创建一个对应的文件对象。然后,我们可以使用Read方法从文件中读取数据,并以字节的形式存储在


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.

Safe Exam Browser
Safe Exam Browser is a secure browser environment for taking online exams securely. This software turns any computer into a secure workstation. It controls access to any utility and prevents students from using unauthorized resources.

Dreamweaver CS6
Visual web development tools

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool






