Python algorithm application practical stack

What is a stack? You can understand it as a first-in-last-out data structure (First In Last Out), a linear table with limited operations. The following article mainly introduces you to the practical application of stack in Python. The article gives multiple examples. Friends in need can refer to it. Let’s take a look together.

Stack(stack)

The stack is also called a stack. It is a special ordered list. The insertion and deletion operations are all in the stack. The operation is carried out on top and according to the rules of first in, first out and last in, first out.

As shown in the picture below

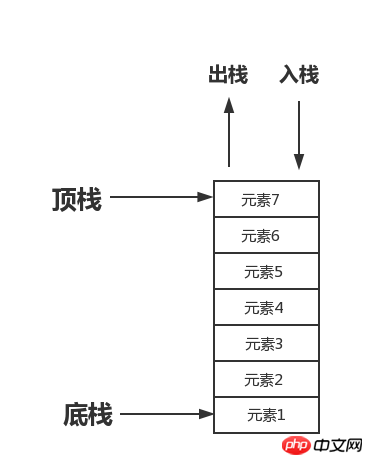
For example, in the magazine of a gun, the first bullet put into the magazine is fired instead When the bullet is fired, it is the last one, and when the last bullet put into the magazine is fired, it is the first bullet fired.

Stack interface

If you create a stack, then you should have the following interface to operate the stack

Interface	Description
push()	Push
pop()	Pop
isEmpty()	Judge whether it is an empty stack
length()	Get the length of the stack
getTop()	Get the element at the top of the stack, the element will not pop out of the stack

#After knowing that the stack requires the above interface, then in Python, the list is similar to a stack, and the interface provided is as follows :

##OperationDescriptions = []Create a stacks.append(x)Add an element to the stacks.pop()Delete an element from the stacknot sDetermine whether the stack is emptylen(s)Get the number of elements in the stacks[-1]Get The element on the top of the stack

##Stack interface usage example in Python:

# 创建一个栈
In [1]: s = []
# 往栈内添加一个元素
In [2]: s.append(1)
In [3]: s
Out[3]: [1]
# 删除栈内的一个元素
In [4]: s.pop()
Out[4]: 1
In [5]: s
Out[5]: []
# 判断栈是否为空
In [6]: not s
Out[6]: True
In [7]: s.append(1)
In [8]: not s
Out[8]: False
# 获取栈内元素的数量
In [9]: len(s)
Out[9]: 1
In [10]: s.append(2)
In [11]: s.append(3)
# 取栈顶的元素
In [12]: s[-1]
Out[12]: 3

A large number of examplesAfter understanding the basic concepts of the stack, let us look at a few more examples to facilitate our understanding of the stack.

Bracket matching

Question

If the expression is allowed to contain three square brackets (), [], {}, the nesting order is Arbitrary, for example:

Correct format

{()[()]},[{({})}]

Incorrect format

[(]),[()),(()}

Write a function to determine whether the bracket matching of an expression string is correct

Idea

Create an empty stack to store items that have not yet been found Left bracket;
Convenience string, when encountering a left bracket, push it onto the stack, when encountering a right bracket, pop a left bracket out of the stack for matching;
During the second step, if the right bracket is encountered when the stack is empty, it means that the left bracket is missing and does not match;
At the end of the second step traversal, the stack is not Empty, indicating that the right bracket is missing and does not match;
Solution code

It is recommended to break points in pycharm for better understanding

#!/use/bin/env python
# _*_ coding:utf-8 _*_
LEFT = {'(', '[', '{'} # 左括号
RIGHT = {')', ']', '}'} # 右括号
def match(expr):
 """
 :param expr: 传过来的字符串
 :return: 返回是否是正确的
 """
 stack = [] # 创建一个栈
 for brackets in expr: # 迭代传过来的所有字符串
 if brackets in LEFT: # 如果当前字符在左括号内
  stack.append(brackets) # 把当前左括号入栈
 elif brackets in RIGHT: # 如果是右括号
  if not stack or not 1 <= ord(brackets) - ord(stack[-1]) <= 2:
  # 如果当前栈为空，()]
  # 如果右括号减去左括号的值不是小于等于2大于等于1
  return False # 返回False
  stack.pop() # 删除左括号
 return not stack # 如果栈内没有值则返回True，否则返回False
result = match(&#39;[(){()}]&#39;)
print(result)

Maze problem

Question

Use a two-dimensional array to represent a simple maze, and use 0 to represent the path. Use 1 to represent blocking. At each point, the mouse can move to the four adjacent points of southeast, northwest and northwest. Design an algorithm to simulate the mouse walking through the maze and find a path from the entrance to the exit.

As shown in the picture

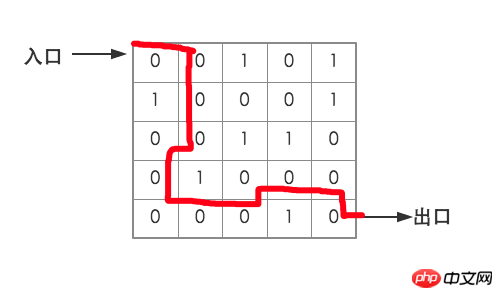The correct route out is shown as the red line in the picture

Thoughts

Use a stack to record the path of the mouse from the entrance to the exit
After reaching a certain point, push the left side of the point onto the stack and set the point value to 1 , indicating that you have passed;
Choose any one of the reachable points from the four adjacent points and walk to that point;
If you don’t move to the 4 nearby points after reaching a certain point, it means you have reached a dead end. At this time, exit the stack and take a step back to try other points;
Repeatedly execute the second, Three or four steps until the exit is found;
Solution code

#!/use/bin/env python
# _*_ coding:utf-8 _*_
def initMaze():
 """
 :return: 初始化迷宫
 """
 maze = [[0] * 7 for _ in range(5 + 2)] # 用列表解析创建一个7*7的二维数组，为了确保迷宫四周都是墙
 walls = [ # 记录了墙的位置
 (1, 3),
 (2, 1), (2, 5),
 (3, 3), (3, 4),
 (4, 2), # (4, 3), # 如果把(4, 3)点也设置为墙，那么整个迷宫是走不出去的，所以会返回一个空列表
 (5, 4)
 ]
 for i in range(7): # 把迷宫的四周设置成墙
 maze[i][0] = maze[i][-1] = 1
 maze[0][i] = maze[-1][i] = 1
 for i, j in walls: # 把所有墙的点设置为1
 maze[i][j] = 1
 return maze
"""
[1, 1, 1, 1, 1, 1, 1]
[1, 0, 0, 1, 0, 0, 1]
[1, 1, 0, 0, 0, 1, 1]
[1, 0, 0, 1, 1, 0, 1]
[1, 0, 1, 0, 0, 0, 1]
[1, 0, 0, 0, 1, 0, 1]
[1, 1, 1, 1, 1, 1, 1]
"""
def path(maze, start, end):
 """
 :param maze: 迷宫
 :param start: 起始点
 :param end: 结束点
 :return: 行走的每个点
 """
 i, j = start # 分解起始点的坐标
 ei, ej = end # 分解结束点的左边
 stack = [(i, j)] # 创建一个栈，并让老鼠站到起始点的位置
 maze[i][j] = 1 # 走过的路置为1
 while stack: # 栈不为空的时候继续走，否则退出
 i, j = stack[-1] # 获取当前老鼠所站的位置点
 if (i, j) == (ei, ej): break # 如果老鼠找到了出口
 for di, dj in [(0, -1), (0, 1), (-1, 0), (1, 0)]: # 左右上下
  if maze[i + di][j + dj] == 0: # 如果当前点可走
  maze[i + di][j + dj] = 1 # 把当前点置为1
  stack.append((i + di, j + dj)) # 把当前的位置添加到栈里面
  break
 else: # 如果所有的点都不可走
  stack.pop() # 退回上一步
 return stack # 如果迷宫不能走则返回空栈
Maze = initMaze() # 初始化迷宫
result = path(maze=Maze, start=(1, 1), end=(5, 5)) # 老鼠开始走迷宫
print(result)
# [(1, 1), (1, 2), (2, 2), (3, 2), (3, 1), (4, 1), (5, 1), (5, 2), (5, 3), (4, 3), (4, 4), (4, 5), (5, 5)]

Suffix expression evaluation

Question

When calculating an expression, the compiler usually uses a suffix expression, which does not require parentheses:

##Infix expressionPostfix expression##2 3 * 42 3 4 * 1 2 6 3 / * 2 18 3 1 2 * /

( 1 2 ) * ( 6 / 3 ) 2

18 / ( 3 * ( 1 2 ) )

编写程序实现后缀表达式求值函数。

思路

1. 建立一个栈来存储待计算的操作数；

2. 遍历字符串，遇到操作数则压入栈中，遇到操作符号则出栈操作数(n次)，进行相应的计算，计算结果是新的操作数压回栈中，等待计算

3. 按上述过程，遍历完整个表达式，栈中只剩下最终结果；
   

解决代码

#!/use/bin/env python
# _*_ coding:utf-8 _*_
operators = { # 运算符操作表
 '+': lambda op1, op2: op1 + op2,
 '-': lambda op1, op2: op1 - op2,
 '*': lambda op1, op2: op1 * op2,
 '/': lambda op1, op2: op1 / op2,
}
def evalPostfix(e):
 """
 :param e: 后缀表达式
 :return: 正常情况下栈内的第一个元素就是计算好之后的值
 """
 tokens = e.split() # 把传过来的后缀表达式切分成列表
 stack = []
 for token in tokens: # 迭代列表中的元素
 if token.isdigit(): # 如果当前元素是数字
  stack.append(int(token)) # 就追加到栈里边
 elif token in operators.keys(): # 如果当前元素是操作符
  f = operators[token] # 获取运算符操作表中对应的lambda表达式
  op2 = stack.pop() # 根据先进后出的原则，先让第二个元素出栈
  op1 = stack.pop() # 在让第一个元素出栈
  stack.append(f(op1, op2)) # 把计算的结果在放入到栈内
 return stack.pop() # 返回栈内的第一个元素
result = evalPostfix('2 3 4 * +')
print(result)
# 14

背包问题

题目

有一个背包能装10kg的物品，现在有6件物品分别为：

物品名称	重量
物品0	1kg
物品1	8kg
物品2	4kg
物品3	3kg
物品4	5kg
物品5	2kg

编写找出所有能将背包装满的解，如物品1+物品5。

解决代码

#!/use/bin/env python
# _*_ coding:utf-8 _*_
def knapsack(t, w):
 """
 :param t: 背包总容量
 :param w: 物品重量列表
 :return:
 """
 n = len(w) # 可选的物品数量
 stack = [] # 创建一个栈
 k = 0 # 当前所选择的物品游标
 while stack or k < n: # 栈不为空或者k<n
 while t > 0 and k < n: # 还有剩余空间并且有物品可装
  if t >= w[k]: # 剩余空间大于等于当前物品重量
  stack.append(k) # 把物品装备背包
  t -= w[k] # 背包空间减少
  k += 1 # 继续向后找
 if t == 0: # 找到了解
  print(stack)
 # 回退过程
 k = stack.pop() # 把最后一个物品拿出来
 t += w[k] # 背包总容量加上w[k]
 k += 1 # 装入下一个物品
knapsack(10, [1, 8, 4, 3, 5, 2])
"""
[0, 2, 3, 5]
[0, 2, 4]
[1, 5]
[3, 4, 5]
"""

The above is the detailed content of Python algorithm application practical stack. For more information, please follow other related articles on the PHP Chinese website!