How to operate red-black tree with JS

This time I will show you how to operate red-black trees with JS, and what are the precautions for operating red-black trees with JS. The following is a practical case, let's take a look.

Properties of red-black trees

A binary search tree that satisfies the following properties is a red-black tree

1. Each node is either black or red.

2. The root node is black.

3. Each leaf node (NIL) is black.

4. If a node is red, both of its child nodes are black.

5. For each node, the simple path from the node to all its descendant leaf nodes contains the same number of black nodes.

Property 1 and Property 2 don’t need to be explained too much.

Property 3, each leaf node (NIL) is black. The leaf nodes here do not refer to nodes 1, 5, 8, and 15 in the above figure, but to the nodes with null values ​​in the figure below. Their color is black and they are the child nodes of their parent nodes. .

Property 4, if a node is red (white is used instead of red in the figure), then its two child nodes are black, such as node 2 ,5,8,15. However, if both child nodes of a node are black, the node may not be red, such as node 1.

Property 5, for each node, the simple path from the node to all its descendant leaf nodes contains the same number of black nodes. For example, on the simple path from node 2 to all its descendant leaf nodes, the number of black nodes is 2; on the simple path from root node 11 to all its descendant leaf nodes, the number of black nodes is 2. is 3.

What are the characteristics of such a tree?

By constraining the color of each node on any simple path from the root to the leaf node, the red-black tree ensures that no path will be twice as long as any other path. Because it is approximately balanced. ——"Introduction to Algorithms"

Due to property 4, two red nodes will not be adjacent in a red-black tree. The shortest possible path in the tree is the path with all black nodes, and the longest possible path in the tree is the path with alternating red nodes and black nodes. Combined with property 5, each path contains the same number of black nodes, so the red-black tree ensures that no path will be twice as long as other paths.

Insertion of red-black tree

First insert the node in a binary search tree and color it red. If it is black, it will violate property 5 and is inconvenient to adjust; if it is red, it may violate property 2 or property 4. It can be restored to the properties of a red-black tree through relatively simple operations.

After a node is inserted in a binary search tree, the following situations may occur:

Scenario 1

Inserting a node Finally, there is no parent node, and the node is inserted to become the root node, which violates property 2. The node is adjusted to black and the insertion is completed.

Case 2

After inserting a node, its parent node is black, and does not violate any properties. No adjustment is required, and the insertion is completed. For example, insert node 13 in the figure below.

Case 3

After inserting a node, its parent node is red, which violates property 4 and requires a series of adjustments. For example, insert node 4 in the figure below.

#So what are the series of adjustments?

If the parent node father of the inserted node node is red, then the node father must have a black parent node grandfather, because if the node father does not have a parent node, it is the root node. point, and the root node is black. Then the other child node of the node grandfather can be called the node uncle, which is the sibling node of the node father. The node uncle may be black or red.

Let’s analyze the simplest situation first, because complex situations can be transformed into simple situations. The simple situation is the situation where the node uncle is black.

Scenario 3.1

As shown in (a) above, the situation is like this, node is red, father is red, grandfather and uncle are black, α, β, θ, ω, and eta are all subtrees corresponding to the nodes. Assume that in the entire binary search tree, only node and father cannot become a normal red-black tree due to violation of property 4. At this time, adjusting picture (a) to picture (b) can restore it to a normal red-black tree. The entire adjustment process is actually divided into two steps, rotation and color change.

What is rotation?

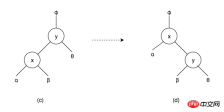
The above picture (c) is part of a binary search tree, where x, y are nodes, α, β, θ are the subtrees of the corresponding nodes . It can be seen from the figure that α

Node is red, father is red, grandfather and uncle are black. Specific situation 1

In Figure (a), node is the left child node of father, and father is the left child of grand. Node, node

Color change

So after the picture (a) is rotated, grand should be changed to red, father should be changed to black, and it should be changed into picture (b) to complete the insertion.

Node is red, father is red, grandfather and uncle are black. Specific situation 2

node is the right child node of father, and father is the right child node of grand, as shown below ( e), is the reversal of specific situation 1.

##That is, uncle Node is red, father is red, grandfather and uncle are black. Specific situation three

node is the right child node of father, and father is the left child node of grand, as shown below ( m).

After rotating node and father in figure (m), it becomes figure (n), and treating father as a new node becomes the specific situation one. Again After rotating and changing color, the insertion is completed.

Node is red, father is red, grandfather and uncle are black. Specific situation 4

node is the right child node of father, and father is the left child node of grand, as shown below ( i), is the reversal of specific situation three.

After rotating the node and father in figure (i), it becomes figure (j). When father is regarded as the new node, it becomes the specific situation 2. Again After rotating and changing color, the insertion is completed.

Scenario 3.2

node, father and uncle are red, grandfather is black.

As shown in the picture above (k), instead of rotating, the grand is colored red, the father and uncle are colored black, and the grand is used as a new node to judge the situation. If grand is used as a new node, it becomes case 2, and the insertion is completed; if it becomes case 3.1, after adjustment, the insertion is completed; if it is still case 3.2, continue to change the color of grand, father and uncle, and node The node moves up. If the new node node has no parent node, it becomes case 1. The root node is colored black, and the insertion is completed.

To sum up

	Node situation	Operation
Situation 1	Node is red, no father	Recolor node
Case 2	Node is red, father is black
Scenario 3.1	node,father is red,grand,uncle is black	Rotate once or twice and recolor
Scenario 3.2	Node, father, uncle are red, grand is black	Recolor father, uncle, grand, and grand is the new node

Code

// 结点
function Node(value) {
 this.value = value
 this.color = 'red' // 结点的颜色默认为红色
 this.parent = null
 this.left = null
 this.right = null
}
function RedBlackTree() {
 this.root = null
}
RedBlackTree.prototype.insert = function (node) {
 // 以二叉搜索树的方式插入结点
 // 如果根结点不存在，则结点作为根结点
 // 如果结点的值小于node，且结点的右子结点不存在，跳出循环
 // 如果结点的值大于等于node，且结点的左子结点不存在，跳出循环
 if (!this.root) {
 this.root = node
 } else {
 let current = this.root
 while (current[node.value  tree.insert(new Node(i)))
debugger

I believe you have mastered the method after reading the case in this article. For more exciting information, please pay attention to other related articles on the php Chinese website!

Recommended reading:

jQuery implements automatic addition of ellipses when the input text exceeds the specified number of lines

EL expression in JS to obtain related elements Parameters

Vue custom dynamic component usage analysis

The above is the detailed content of How to operate red-black tree with JS. For more information, please follow other related articles on the PHP Chinese website!