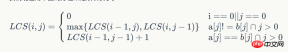This time I will show you how to make a public subsequence in JS. What are the precautions for implementing a public subsequence in JS? The following is a practical case, let's take a look.
Introduction
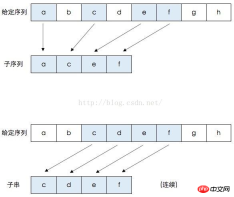
The Longest Common Subsequence LCS is to extract all the possible subsequences from the given two sequences X and Y. The possible extra characters are arranged in the order in which they are arranged in the original sequence. The algorithm for LCS problems has a wide range of uses. For example, in the management of different versions of software, the LCS algorithm is used to find the similarities and differences between the old and new versions; in software testing, the LCS algorithm is used to compare recorded and played back sequences. In the field of genetic engineering, the LCS algorithm is used The algorithm checks the similarities and differences between the patient's DNA strand and the bond's DNA strand; in the anti-plagiarism system, the LCS algorithm is used to check the plagiarism rate of the paper. The LCS algorithm can also be used for program code similarity measurement, human running sequence retrieval, video segment matching, etc., so research on the LCS algorithm has high application value. Subsequence: A subsequence of a specific sequence is a subsequence of a given sequence. The result obtained by removing zero or more elements (without changing the relative order between elements). For example, the subsequences of the sequence are: , , Common subsequence: Given sequences X and Y, sequence Z is a subsequence of X and a subsequence of Y, then Z is the common subsequence of X and Y. For example, X=[A,B,C,B,D,A,B], Y=[B,D,C,A,B,A[, then the sequence Z=[B,C,A] is X and Y The common subsequence of , its length is 3. But Z is not the longest common subsequence of X and Y, and the sequences [B, C, B, A] and [B, D, A, B] are also the longest common subsequences of X and Y, with a length of 4 , and X and Y do not have a common subsequence with a length greater than or equal to 5. For the common subsequences of the sequence [A, B, C] and the sequence [E, F, G], there is only the empty sequence []. Longest common subsequence: Given the sequences X and Y, select the one or several with the longest length from all their common subsequences.Substring: A new series formed by deleting zero or several characters from the front or the end of a sequence, or both at the same time. The difference is that subsequences can have characters cut out from the middle. How many neutron sequences are there in this
string of cnblogs? Obviously there are 27 of them, such as cb, cgs, etc. are all their subsequences
Problem Analysis
We still start the analysis from a matrix and derive the state transition equation ourselves. First of all, we convert the problem into a concept that is familiar enough to the front end. Instead of calling it serially, it can be thought of as an array or a string. To keep things simple, let's just assume that two strings are being compared. We focus on the concept of "subsequence", which can delete multiple or zero ones, or all of them. At this time our first subsequence is an empty string (if our sequence is not a string, we can still)! This is something you really need to pay attention to! Many people just can't understand the chart in "Introduction to Algorithms", and there are also many bloggers who pretend to understand. We always compare from left to right, and of course the first string, because it is the height of the matrix, is placed vertically.The above is the detailed content of How to make a public subsequence in JS. For more information, please follow other related articles on the PHP Chinese website!
 The Origins of JavaScript: Exploring Its Implementation LanguageApr 29, 2025 am 12:51 AM
The Origins of JavaScript: Exploring Its Implementation LanguageApr 29, 2025 am 12:51 AMJavaScript originated in 1995 and was created by Brandon Ike, and realized the language into C. 1.C language provides high performance and system-level programming capabilities for JavaScript. 2. JavaScript's memory management and performance optimization rely on C language. 3. The cross-platform feature of C language helps JavaScript run efficiently on different operating systems.
 Behind the Scenes: What Language Powers JavaScript?Apr 28, 2025 am 12:01 AM
Behind the Scenes: What Language Powers JavaScript?Apr 28, 2025 am 12:01 AMJavaScript runs in browsers and Node.js environments and relies on the JavaScript engine to parse and execute code. 1) Generate abstract syntax tree (AST) in the parsing stage; 2) convert AST into bytecode or machine code in the compilation stage; 3) execute the compiled code in the execution stage.
 The Future of Python and JavaScript: Trends and PredictionsApr 27, 2025 am 12:21 AM
The Future of Python and JavaScript: Trends and PredictionsApr 27, 2025 am 12:21 AMThe future trends of Python and JavaScript include: 1. Python will consolidate its position in the fields of scientific computing and AI, 2. JavaScript will promote the development of web technology, 3. Cross-platform development will become a hot topic, and 4. Performance optimization will be the focus. Both will continue to expand application scenarios in their respective fields and make more breakthroughs in performance.
 Python vs. JavaScript: Development Environments and ToolsApr 26, 2025 am 12:09 AM
Python vs. JavaScript: Development Environments and ToolsApr 26, 2025 am 12:09 AMBoth Python and JavaScript's choices in development environments are important. 1) Python's development environment includes PyCharm, JupyterNotebook and Anaconda, which are suitable for data science and rapid prototyping. 2) The development environment of JavaScript includes Node.js, VSCode and Webpack, which are suitable for front-end and back-end development. Choosing the right tools according to project needs can improve development efficiency and project success rate.
 Is JavaScript Written in C? Examining the EvidenceApr 25, 2025 am 12:15 AM
Is JavaScript Written in C? Examining the EvidenceApr 25, 2025 am 12:15 AMYes, the engine core of JavaScript is written in C. 1) The C language provides efficient performance and underlying control, which is suitable for the development of JavaScript engine. 2) Taking the V8 engine as an example, its core is written in C, combining the efficiency and object-oriented characteristics of C. 3) The working principle of the JavaScript engine includes parsing, compiling and execution, and the C language plays a key role in these processes.
 JavaScript's Role: Making the Web Interactive and DynamicApr 24, 2025 am 12:12 AM
JavaScript's Role: Making the Web Interactive and DynamicApr 24, 2025 am 12:12 AMJavaScript is at the heart of modern websites because it enhances the interactivity and dynamicity of web pages. 1) It allows to change content without refreshing the page, 2) manipulate web pages through DOMAPI, 3) support complex interactive effects such as animation and drag-and-drop, 4) optimize performance and best practices to improve user experience.
 C and JavaScript: The Connection ExplainedApr 23, 2025 am 12:07 AM
C and JavaScript: The Connection ExplainedApr 23, 2025 am 12:07 AMC and JavaScript achieve interoperability through WebAssembly. 1) C code is compiled into WebAssembly module and introduced into JavaScript environment to enhance computing power. 2) In game development, C handles physics engines and graphics rendering, and JavaScript is responsible for game logic and user interface.
 From Websites to Apps: The Diverse Applications of JavaScriptApr 22, 2025 am 12:02 AM
From Websites to Apps: The Diverse Applications of JavaScriptApr 22, 2025 am 12:02 AMJavaScript is widely used in websites, mobile applications, desktop applications and server-side programming. 1) In website development, JavaScript operates DOM together with HTML and CSS to achieve dynamic effects and supports frameworks such as jQuery and React. 2) Through ReactNative and Ionic, JavaScript is used to develop cross-platform mobile applications. 3) The Electron framework enables JavaScript to build desktop applications. 4) Node.js allows JavaScript to run on the server side and supports high concurrent requests.


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.

WebStorm Mac version
Useful JavaScript development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Dreamweaver Mac version
Visual web development tools

Atom editor mac version download
The most popular open source editor




 ##×
##×