Home >Backend Development >PHP Tutorial >PHP heap implements TopK algorithm example
PHP heap implements TopK algorithm example
- 小云云Original
- 2018-03-16 15:22:432114browse
Binary heap is a special kind of heap. A binary heap is a complete binary tree or an approximately complete binary tree. There are two types of binary heaps, maximum heap and minimum heap. Maximum heap: the key value of the parent node is always greater than Or equal to the key value of any child node; minimum heap: the key value of the parent node is always less than or equal to the key value of any child node.
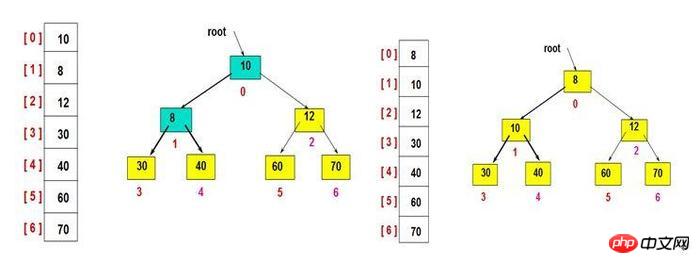
Small top heap-(picture from the Internet)
Binary heap is generally represented by an array (see the picture above), For example, the position of the root node in the array is 0, and the child nodes at the nth position are at 2n+1 and 2n+2 respectively. Therefore, the child nodes at the 0th position are at 1 and 2, and the child nodes of 1 are at 3 and 2n+2. 4. By analogy, this storage method facilitates finding parent nodes and child nodes.
I won’t go into details about the specific conceptual issues here. If you have any questions about the binary heap, you can have a good understanding of this data structure. Next, we will use PHP code to implement and solve the above topN problems. , in order to see the difference, let’s first use the sorting method to see the effect.
Use quick sorting algorithm to implement TopN
//为了测试运行内存调大一点ini_set('memory_limit', '2024M');//实现一个快速排序函数function quick_sort(array $array){
$length = count($array); $left_array = array(); $right_array = array(); if($length <= 1){ return $array;
} $key = $array[0]; for($i=1;$i<$length;$i++){ if($array[$i] > $key){ $right_array[] = $array[$i];
}else{ $left_array[] = $array[$i];
}
} $left_array = quick_sort($left_array); $right_array = quick_sort($right_array); return array_merge($right_array,array($key),$left_array);
}//构造500w不重复数for($i=0;$i<5000000;$i++){ $numArr[] = $i;
}//打乱它们shuffle($numArr);//现在我们从里面找到top10最大的数var_dump(time());
print_r(array_slice(quick_sort($all),0,10));
var_dump(time());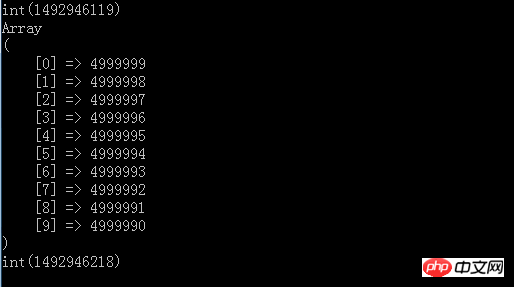
You can see the result after running
The top10 results are printed above, and the running time is output, which is about 99s. However, this is only the case when 5 million numbers can be loaded into the memory. If we have a file with 5kw or 500 million numbers, it will definitely be There will be some problems.
Use the binary heap algorithm to implement TopN
The implementation process is:
1. First read 10 or 100 numbers into the array, This is our topN number.
2. Call the generate small top heap function to generate a small top heap structure from this array. At this time, the top of the heap must be the smallest.
3. Traverse the remaining files or arrays in sequence All numbers.
4. Each time one is traversed, the size is compared with the element at the top of the heap. If it is smaller than the element at the top of the heap, discard it. If it is greater than the element at the top of the heap, replace it.
5. Replace with the element at the top of the heap. After completion, call the generate small top heap function to continue to generate the small top heap, because we need to find the smallest one.
6. Repeat the above 4~5 steps, so that after all traversals are completed, the inside of our small top heap is the largest topN, because our small top heap always excludes the smallest and leaves the largest, and the adjustment of the small top heap is also very fast. It is just a relative adjustment, as long as the root node is smaller than the left and right nodes.
7. In terms of algorithm complexity, the worst case scenario is top 10. Every time a number is traversed, if it is replaced with the top of the heap, it needs to be adjusted 10 times. This is faster than the sorting speed, and not all the contents are included. Read all into the memory, you can understand that the achievement is a linear traversal.
//生成小顶堆函数function Heap(&$arr,$idx){
$left = ($idx << 1) + 1; $right = ($idx << 1) + 2; if (!$arr[$left]){ return;
} if($arr[$right] && $arr[$right] < $arr[$left]){ $l = $right;
}else{ $l = $left;
} if ($arr[$idx] > $arr[$l]){ $tmp = $arr[$idx];
$arr[$idx] = $arr[$l]; $arr[$l] = $tmp;
Heap($arr,$l);
}
}//这里为了保证跟上面一致,也构造500w不重复数/*
当然这个数据集并不一定全放在内存,也可以在
文件里面,因为我们并不是全部加载到内存去进
行排序
*/for($i=0;$i<5000000;$i++){ $numArr[] = $i;
}//打乱它们shuffle($numArr);//先取出10个到数组$topArr = array_slice($numArr,0,10);//获取最后一个有子节点的索引位置//因为在构造小顶堆的时候是从最后一个有左或右节点的位置//开始从下往上不断的进行移动构造(具体可看上面的图去理解)$idx = floor(count($topArr) / 2) - 1;//生成小顶堆for($i=$idx;$i>=0;$i--){
Heap($topArr,$i);
}
var_dump(time());//这里可以看到,就是开始遍历剩下的所有元素for($i = count($topArr); $i < count($numArr); $i++){ //每遍历一个则跟堆顶元素进行比较大小
if ($numArr[$i] > $topArr[0]){ //如果大于堆顶元素则替换
$topArr[0] = $numArr[$i]; /*
重新调用生成小顶堆函数进行维护,只不过这次是从堆顶
的索引位置开始自上往下进行维护,因为我们只是把堆顶
的元素给替换掉了而其余的还是按照根节点小于左右节点
的顺序摆放这也就是我们上面说的,只是相对调整下,并
不是全部调整一遍
*/
Heap($topArr,0);
}
}
var_dump(time());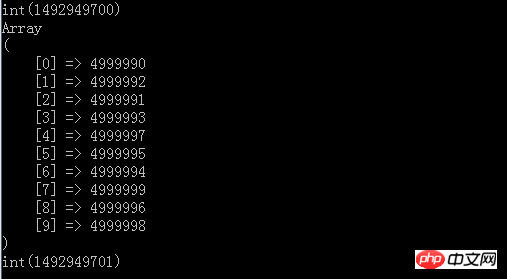
The result after running
You can see that the final result is also top10, but the time It only takes about 1 second, and both memory and time efficiency meet our requirements. And the best thing about sorting is that we don’t need to read all the data sets into the memory, because we don’t need to sort, and the above It is for demonstration, so 5 million elements are constructed directly in the memory. However, we can transfer all of them to a file, and then read them line by line for comparison, because the core point of our data structure is linear traversal and small memory. Compare the small top heap structure and finally get TopN.
End
The last thing I want to say isAlgorithm + Data Structure It is really important, a good Algorithms can greatly improve our efficiency.
The above is the detailed content of PHP heap implements TopK algorithm example. For more information, please follow other related articles on the PHP Chinese website!

