Dijkstra shortest path implemented in PHP

This article mainly introduces the Dijkstra shortest path algorithm implemented in PHP, briefly describes the concept and function of Dijkstra shortest path algorithm, and analyzes the Dijkstra shortest path algorithm implemented in PHP based on specific examples. (Dijkstra) shortest path algorithm related steps and operating skills, friends in need can refer to

This article describes the Dijkstra (Dijkstra) shortest path algorithm implemented in PHP. Share it with everyone for your reference, the details are as follows:

1. Problems to be solved

The single-source shortest path problem, in a given direction The problem of finding the shortest path from one vertex (single source vertex) to all other vertices in the graph. In the figure below, there is a weight on each edge, and we hope to find the shortest path from A to all other vertices (B/C/D/E/F/G).

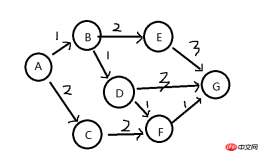
2. Problem analysis (the substructure of the shortest path is also optimal)

If P (A,G) is the shortest path from vertex A to G. Assuming that D and F are the midpoints on this path, then P(D,F) must be the shortest path from D to F. If P(D,F) is not the shortest path from D to F, then there must be another path from D to F from a certain node M that can make P(A,B...M...F,G) faster than P (A,G) is small and contradictory.

With this property, we can understand Dijkstra's algorithm.

3. Dijkstra algorithm

Dijkstra algorithm, also called Dijkstra algorithm (Dijkstra), also called single source shortest path algorithm, The so-called single source is the problem of finding the shortest path from a vertex to all reachable vertices in a directed graph. The problem is described as assuming that G = (V, E) is a directed graph, V represents the vertex and E represents the edge. Each of its edges (i, j) belongs to E and has a non-negative weight W (I, j). Specifying a node v0 in G requires connecting every link from v0 to G to vj (vj belongs to V ) find the shortest directed path (or point out that it does not exist). Dijstra's algorithm uses a greedy strategy, starting from the source point, and constantly finding the shortest distance to other points through connected points.

Dijkstra's greedy application uses the properties in (2), constantly selecting the "nearest" nodes and testing all possible links of each node, expanding outward layer by layer with the starting point as the center, until it extends to the end point. For source point A, gradually expand, and update the vertex information directly adjacent to i according to dist[j]=min{dist[j],dist[i]+matrix[i][j]}.

Algorithm description

1) Algorithm idea:

Suppose G=(V,E) is a weighted directed graph, and put the The vertex set V is divided into two groups. The first group is the vertex set for which the shortest path has been found (represented by S. Initially, there is only one source point in S. Afterwards, each shortest path is found, it will be added to the set S until All vertices are added to S, and the algorithm ends). The second group is the remaining set of vertices for which the shortest path has not been determined (represented by U). The vertices of the second group are added to S in order of increasing shortest path length. During the joining process, the length of the shortest path from the source point v to each vertex in S is always maintained to be no greater than the length of the shortest path from the source point v to any vertex in U. In addition, each vertex corresponds to a distance. The distance of the vertex in S is the shortest path length from v to this vertex. The distance of the vertex in U is the current path from v to this vertex that only includes the vertices in S as intermediate vertices. The shortest path length.

2) Algorithm steps:

a. Initially, S only contains the source point, that is, S={v}, and the distance of v is 0. U contains other vertices except v, that is: U={other vertices}. If v has an edge with vertex u in U, then has a normal weight value. If u is not an outgoing edge adjacent point of v, Then the weight of is ∞.

b. Select a vertex k from U with the smallest distance v, and add k to S (the selected distance is the shortest path length from v to k).

c. Taking k as the newly considered intermediate point, modify the distance of each vertex adjacent to k in U; ​​if the distance from source point v to vertex u (passing vertex k) is longer than the original distance (not After passing vertex k) short, modify the distance value of vertex u. The modified distance value is the distance of vertex k plus the weight of the edge between k and u.

d. Repeat steps b and c until all vertices are included in S.

4. Algorithm PHP implementation

##

<?php
class Dijkstra
{
  private $G;
  public function __construct()
  {
    //有向图存储
    $this->G = array(
      array(0,1,2,0,0,0,0),
      array(0,0,0,1,2,0,0),
      array(0,0,0,0,0,2,0),
      array(0,0,0,0,0,1,3),
      array(0,0,0,0,0,0,3),
      array(0,0,0,0,0,0,1),
      array(0,0,0,0,0,0,0),
    );
  }
  public function calculate()
  {
    // 存储已经选择节点和剩余节点
    $U = array(0);
    $V = array(1,2,3,4,5,6);
    // 存储路径上节点距离源点的最小距离
    $d = array();
    //初始化图中节点与源点0的最小距离
    for($i=1;$i<7;$i++)
    {
      if($this->G[0][$i]>0)
      {
        $d[$i] = $this->G[0][$i];
      }
      else
      {
        $d[$i] = 1000000;
      }
    }
    // n-1次循环完成转移节点任务
    for($l=0;$l<6;$l++)
    {
      // 查找剩余节点中距离源点最近的节点v
      $current_min = 100000;
      $current_min_v = 0;
      foreach($V as $k=>$v)
      {
        if($d[$v] < $current_min)
        {
          $current_min = $d[$v];
          $current_min_v = $v;
        }
      }
      //从V中更新顶点到U中
      array_push($U,$current_min_v);
      array_splice($V,array_search($current_min_v,$V),1);
      //更新
      foreach($V as $k=>$u)
      {
        if($this->G[$current_min_v][$u]!=0&&$d[$u]>$d[$current_min_v]+$this->G[$current_min_v][$u])
        {
          $d[$u] = $d[$current_min_v]+$this->G[$current_min_v][$u];
        }
      }
    }
    foreach($d as $k => $u)
    {
      echo $k.&#39;=>&#39;.$u.&#39;<br>&#39;;
    }
  }
}
?>

Calling class:

$D = new Dijkstra;
$D->calculate();

Execution result:

1=>1
2=>2
3=>2
4=>3
5=>3
6=>4

The above is the detailed content of Dijkstra shortest path implemented in PHP. For more information, please follow other related articles on the PHP Chinese website!