Summary of eight sorting algorithms implemented in Python (Part 1)

This article mainly introduces the first of the eight sorting algorithms implemented in Python in detail. It has a certain reference value. Interested friends can refer to it

Sort

Sorting is an operation that is often performed in computers. Its purpose is to adjust a set of "unordered" record sequences into an "ordered" record sequence. Divided into internal sorting and external sorting. If the entire sorting process can be completed without accessing external memory, then this sorting problem is called internal sorting. On the contrary, if the number of records participating in the sorting is very large and the sorting process of the entire sequence cannot be completely completed in the memory and requires access to external memory, this kind of sorting problem is called external sorting. The process of internal sorting is a process of gradually expanding the length of the ordered sequence of records.

Look at the picture to make your understanding clearer and deeper:

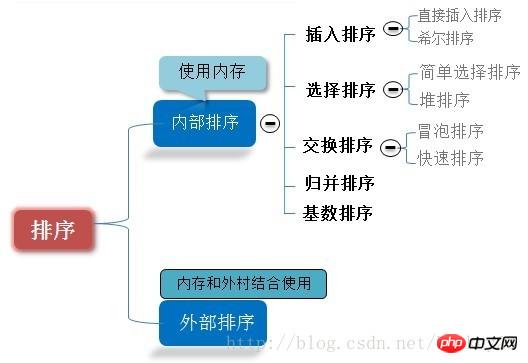
# Assume that there are multiple records with the same keywords in the record sequence to be sorted. If After sorting, the relative order of these records remains unchanged, that is, in the original sequence, ri=rj, and ri is before rj, and in the sorted sequence, ri is still before rj, then this sorting algorithm is said to be stable. ;Otherwise it is called unstable.

Common sorting algorithms

Quick sort, Hill sort, heap sort, and direct selection sort are not stable sorting algorithms, while radix sort, bubble sort, and direct insertion Sorting, half insertion sort, and merge sort are stable sorting algorithms

This article will use Python to implement bubble sort, insertion sort, Hill sort, quick sort, direct selection sort, heap sort, merge sort, and radix sort. These eight sorting algorithms.

1. Bubble Sort

Algorithm principle:

It is known that a set of unordered data a[1], a[ 2],...a[n], they need to be sorted in ascending order. First compare the values ​​​​of a[1] and a[2]. If a[1] is greater than a[2], exchange the values ​​​​of the two, otherwise they will remain unchanged. Then compare the values ​​​​of a[2] and a[3]. If a[2] is greater than a[3], exchange the values ​​​​of the two, otherwise they will remain unchanged. Then compare a[3] and a[4], and so on, and finally compare the values ​​of a[n-1] and a[n]. After one round of processing, the value of a[n] must be the largest in this set of data. If a[1]~a[n-1] is processed in the same way again, the value of a[n-1] must be the largest among a[1]~a[n-1]. Then process a[1]~a[n-2] in the same way for one round, and so on. After a total of n-1 rounds of processing, a[1], a[2],...a[n] are arranged in ascending order. Descending sorting is similar to ascending sorting. If a[1] is less than a[2], the values ​​of the two are exchanged. Otherwise, they remain unchanged, and so on. In general, after each round of sorting, the largest (or smallest) number will be moved to the end of the data sequence, and theoretically a total of n(n-1)/2 exchanges will be performed.

Advantages: Stable;
Disadvantages: Slow, only two adjacent data can be moved at a time.

Python code implementation:

#!/usr/bin/env python
#coding:utf-8
'''
file:python-8sort.py
date:9/1/17 9:03 AM
author:lockey
email:lockey@123.com
desc:python实现八大排序算法
'''
lst1 = [2,5435,67,445,34,4,34]
def bubble_sort_basic(lst1):
 lstlen = len(lst1);i = 0
 while i < lstlen:
  for j in range(1,lstlen):
   if lst1[j-1] > lst1[j]:
   #对比相邻两个元素的大小，小的元素上浮
    lst1[j],lst1[j-1] = lst1[j-1],lst1[j]
  i += 1
  print &#39;sorted{}: {}&#39;.format(i, lst1)
 print &#39;-------------------------------&#39;
 return lst1
bubble_sort_basic(lst1)

Improvement of bubble sort algorithm

For sequences that are completely disordered or have no repeating elements, the above algorithm has no room for improvement based on the same idea. However, if there are repeating elements in a sequence or some elements are in order, in this case there will inevitably be unnecessary Repeated sorting, then we can add a symbolic variable change in the sorting process to mark whether there is data exchange during a certain sorting process. If there is no data exchange during a certain sorting process, it means that the data has been If the arrangement is required, the sorting can be ended immediately to avoid unnecessary comparison process. The improved sample code is as follows:

lst2 = [2,5435,67,445,34,4,34]
def bubble_sort_improve(lst2):
 lstlen = len(lst2)
 i = 1;times = 0
 while i > 0:
  times += 1
  change = 0
  for j in range(1,lstlen):
   if lst2[j-1] > lst2[j]:
   #使用标记记录本轮排序中是否有数据交换
    change = j
    lst2[j],lst2[j-1] = lst2[j-1],lst2[j]
  print 'sorted{}: {}'.format(times,lst2)
  #将数据交换标记作为循环条件，决定是否继续进行排序
  i = change
 return lst2
bubble_sort_improve(lst2)

The running screenshots in the two cases are as follows:

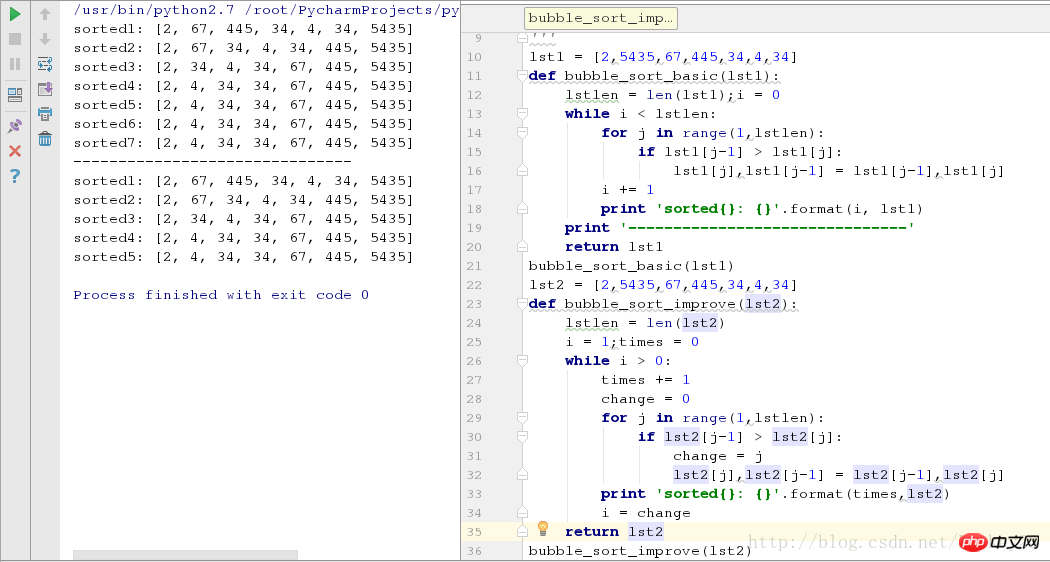
As can be seen from the above figure, for sequences where some elements are arranged in order, the optimized algorithm reduces two rounds of sorting.

2. Selection Sort

Algorithm principle:

In each pass, select the smallest (or The largest element is placed at the end of the sorted array until all the data elements to be sorted are exhausted.
Direct selection sorting of files with n records can obtain ordered results through n-1 direct selection sorting:

①Initial state: The unordered area is R[1..n], ordered The area is empty.
②The first sorting
Select the record R[k] with the smallest keyword in the unordered area R[1..n], and combine it with the first record R[1] in the unordered area Exchange, so that R[1..1] and R[2..n] become a new ordered area with the number of records increased by 1 and a new unordered area with the number of records reduced by 1 respectively.
……
③i-th sorting
When the i-th sorting starts, the current ordered area and unordered area are R[1..i-1] and R(1≤i≤n respectively -1). This sorting operation selects the record R[k] with the smallest key from the current disordered area, and exchanges it with the first record R in the disordered area, so that R[1..i] and R become record numbers respectively. The number of new ordered areas increases by 1 and the number of records decreases by 1. The new unordered area.
In this way, direct selection sorting of files with n records can obtain ordered results through n-1 direct selection sorting.

优点：移动数据的次数已知（n-1次）；
缺点：比较次数多，不稳定。

python代码实现：

# -*- coding: UTF-8 -*-
'''
Created on 2017年8月31日
Running environment：win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def selection_sort(lst):
 lstlen = len(lst)
 for i in range(0,lstlen):
  min = i
  for j in range(i+1,lstlen):
  #从 i+1开始循环遍历寻找最小的索引
   if lst[min] > lst[j]:
    min = j
  lst[min],lst[i] = lst[i],lst[min]
  #一层遍历结束后将最小值赋给外层索引i所指的位置，将i的值赋给最小值索引  
  print('The {} sorted: {}'.format(i+1,lst))
 return lst
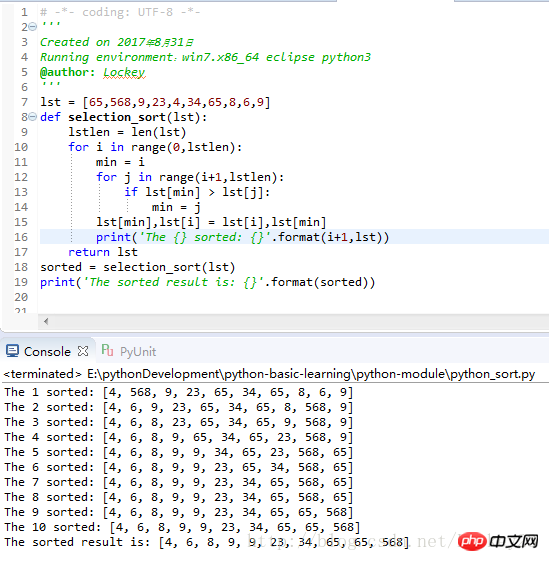
sorted = selection_sort(lst)
print('The sorted result is: {}'.format(sorted))

运行结果截图：

3. 插入排序

算法原理：

已知一组升序排列数据a[1]、a[2]、……a[n]，一组无序数据b[1]、b[2]、……b[m]，需将二者合并成一个升序数列。首先比较b[1]与a[1]的值，若b[1]大于a[1]，则跳过，比较b[1]与a[2]的值，若b[1]仍然大于a[2]，则继续跳过，直到b[1]小于a数组中某一数据a[x]，则将a[x]~a[n]分别向后移动一位，将b[1]插入到原来a[x]的位置这就完成了b[1]的插入。b[2]~b[m]用相同方法插入。（若无数组a，可将b[1]当作n=1的数组a）
优点：稳定，快；
缺点：比较次数不一定，比较次数越多，插入点后的数据移动越多，特别是当数据总量庞大的时候，但用链表可以解决这个问题。

算法复杂度

如果目标是把n个元素的序列升序排列，那么采用插入排序存在最好情况和最坏情况。最好情况就是，序列已经是升序排列了，在这种情况下，需要进行的比较操作需（n-1）次即可。最坏情况就是，序列是降序排列，那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数加上 (n-1）次。平均来说插入排序算法的时间复杂度为O(n^2）。因而，插入排序不适合对于数据量比较大的排序应用。但是，如果需要排序的数据量很小，例如，量级小于千，那么插入排序还是一个不错的选择。

python代码实现：

# -*- coding: UTF-8 -*-
'''
Created on 2017年8月31日
Running environment：win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def insert_sort(lst):
 count = len(lst)
 for i in range(1, count):
  key = lst[i]
  j = i - 1
  while j >= 0:
   if lst[j] > key:
    lst[j + 1] = lst[j]
    lst[j] = key
   j -= 1
  print('The {} sorted: {}'.format(i,lst))
 return lst
sorted = insert_sort(lst)
print('The sorted result is: {}'.format(sorted))

运行结果截图：

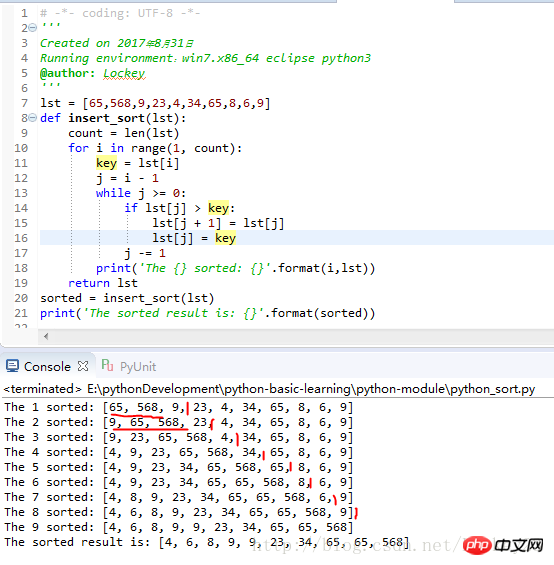
由排序过程可知，每次往已经排好序的序列中插入一个元素，然后排序，下次再插入一个元素排序。。。直到所有元素都插入，排序结束

4. 希尔排序

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL．Shell于1959年提出而得名。

算法原理

算法核心为分组（按步长）、组内插入排序

已知一组无序数据a[1]、a[2]、……a[n]，需将其按升序排列。发现当n不大时，插入排序的效果很好。首先取一增量d(d

python代码实现：

#!/usr/bin/env python
#coding:utf-8
'''
file:python-8sort.py
date:9/1/17 9:03 AM
author:lockey
email:lockey@123.com
desc:python实现八大排序算法
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def shell_sort(lists):
 print 'orginal list is {}'.format(lst)
 count = len(lists)
 step = 2
 times = 0
 group = int(count/step)
 while group > 0:
  for i in range(0, group):
   times += 1
   j = i + group
   while j < count:
    k = j - group
    key = lists[j]
    while k >= 0:
     if lists[k] > key:
      lists[k + group] = lists[k]
      lists[k] = key
     k -= group
    j += group
    print &#39;The {} sorted: {}&#39;.format(times,lists)
  group = int(group/step)
 print &#39;The final result is: {}&#39;.format(lists)
 return lists
shell_sort(lst)

运行测试结果截图：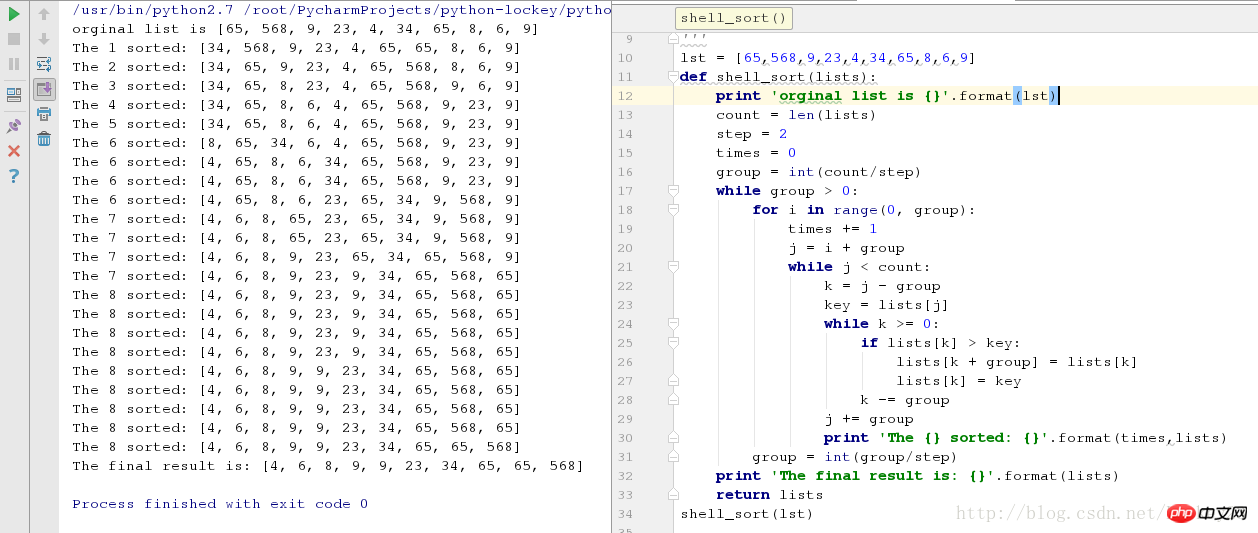

过程分析：

第一步：

1-5：将序列分成了5组（group = int(count/step)）,如下图，一列为一组：

然后各组内进行插入排序，经过5（5组*1次）次组内插入排序得到了序列：

The 1-5 sorted：[34, 65, 8, 6, 4, 65, 568, 9, 23, 9]

第二步：

6666-7777：将序列分成了2组（group = int(group/step)）,如下图，一列为一组：

 

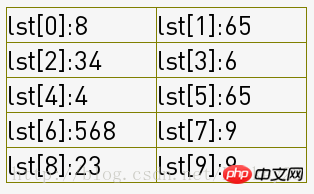
然后各组内进行插入排序，经过8（2组*4次）次组内插入排序得到了序列：

The 6-7 sorted: [4, 6, 8, 9, 23, 9, 34, 65, 568, 65]

第三步：

888888888：对上一个排序结果得到的完整序列进行插入排序：

[4, 6, 8, 9, 23, 9, 34, 65, 568, 65]

经过9（1组*10 -1）次插入排序后：

The final result is: [4, 6, 8, 9, 9, 23, 34, 65, 65, 568]

Hill sorting timeliness analysis is difficult. The number of key code comparisons and the number of recorded moves depend on the selection of the incremental factor sequence. Under certain circumstances, the number of key code comparisons and the number of recorded moves can be accurately estimated. No one has yet given a method for selecting the best incremental factor sequence. The incremental factor sequence can be taken in various ways, including odd numbers and prime numbers. However, it should be noted that there are no common factors among the incremental factors except 1, and the last incremental factor must be 1. Hill sorting method is an unstable sorting method

The above is the detailed content of Summary of eight sorting algorithms implemented in Python (Part 1). For more information, please follow other related articles on the PHP Chinese website!