Detailed explanation of binary and bit operations in Java

1. Representation method:

In the Java language, binary numbers are represented using two's complement, the highest bit is the sign bit, the sign bit of positive numbers is 0, and the sign bit of negative numbers is 1. The representation of the complement code needs to meet the following requirements.

(1) The highest bit of a positive number is 0, and the remaining bits represent the value itself (binary number).

(2) For a negative number, the complement of the absolute value of the number is bitwise inverted, and then 1 is added to the entire number.

2.Bit operator 　

Bit operationExpression consists of operands and bit operators to implement the integer type performs bit operations on binary numbers. Bit operators can be divided into logical operators (including ~, &, | and ^) and shift operators (including >>, << and >>>).

1) The left shift operator (<<) can move the operand on the left side of the operator to the left by the number of digits specified on the right side of the operator (filling 0 in the low bit).

2) The "signed" right shift operator (>>) moves the operand on the left side of the operator to the right by the number of digits specified on the right side of the operator. The "signed" right shift operator uses "sign extension": if the value is positive, 0 is inserted in the high bit; if the value is negative, 1 is inserted in the high bit.

3) Java has also added an "unsigned" right shift operator (>>>), which uses "zero extension": regardless of whether it is positive or negative, 0s are inserted in the high bits. This operator is not available in C or C++.

4) If char, byte or short are shifted, they will be automatically converted into an int before the shift is performed. Only the 5 low bits on the right are used. This prevents us from moving an unrealistic number of digits within an int. If a long value is processed, the final result obtained is also long. At this time, only the 6 low bits on the right will be used to prevent the movement from exceeding the number of ready-made digits in the long value. But you may also encounter a problem when performing "unsigned" right shifts. If you perform a right shift operation on a byte or short value, the result may not be correct (especially Java 1.0 and Java 1.1). They are automatically converted to type int and shifted right. But "zero extension" doesn't happen, so you get a result of -1 in those cases.

Binary is a number system widely used in computing technology. Binary data is a number represented by two digits, 0 and 1. Its base is 2, the carry rule is "every two is forwarded to one", and the borrowing rule is "borrow one to be equal to two", which was discovered by Leibniz, the German master of mathematical philosophy in the 18th century. The current computer system basically uses a binary system, and data is mainly stored in computers in the form of two's complement codes. The binary system in the computer is a very tiny switch, with "on" representing 1 and "off" representing 0.

So what does binary look like in Java? Let us uncover its mysterious veil together.

---

1. Java’s built-in base conversion

The basic calculation methods of converting decimal to binary and binary to decimal will not be expanded on here. said.

There are several methods built into Java to help us perform various hexadecimal conversions. As shown in the figure below (taking Integer integer as an example, other types are the same):

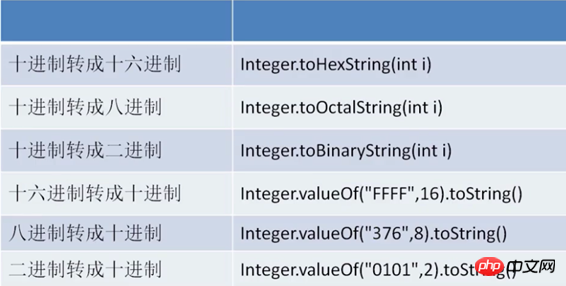
1, converted from decimal to other bases:

1 二进制：Integer.toHexString(int i);2 八进制：Integer.toOctalString(int i);3 十六进制：Integer.toBinaryString(int i);

2. Convert other bases to decimal:

1 二进制：Integer.valueOf("0101",2).toString;2 八进制：Integer.valueOf("376",8).toString;3 十六进制：Integer.valueOf("FFFF",16).toString;

3. Use the parseInt() method and valueOf() method in the Integer class to convert other bases to decimal.

The difference is that the return value of the parseInt() method is of type int, while the return value of valueOf() is an Integer object.

---

2. Basic bit operations

Binary can add, subtract, multiply and divide just like decimal, but it also has a simpler operation method - bit operations. For example, the size of the int type in computers is 32 bits, which can be represented by 32-bit binary numbers, so we can use bit operations to calculate int type values. Of course, you can also use ordinary methods to calculate some data, here I mainly introduce to you the methods of bit operations. We will find that bit operations have incomparable power with ordinary operation methods. For more applications of bit operations, please move to my next blog post "Magical Bit Operations"

First, let's take a look at the basic Operators of bit operations:

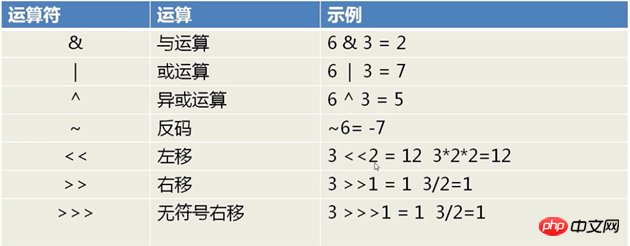
Advantages:

• In certain circumstances, calculation is convenient, fast, and widely supported

• If you use arithmetic methods, the speed is slow and the logic is complicated

• Bitwise operations are not limited to one language, it is the basic operation method of computers

##>>>> >>>>>>>>>>>>>>>>>>>>>>>>> >>>>>>>>>>>>>>>>>>>>>>>>>

(1) The bitwise sum of the two bits of &

is all 1, and the result is 1

0&0=0; 0&1= 0;1&0=0;1&1=1

For example: 51&5 is 0011 0011 & 0000 0101 =0000 0001 Therefore 51&5=1.

Special usage

(1)

Clear. If you want to clear a unit to zero, even if all its binary bits are 0, just AND it with a value whose bits are all zero, and the result will be zero.

(2)

Get the specified position in a number.

For example: Suppose X=10101110, take the lower four digits of X, and use

Method: Find a number that corresponds to the bit that x needs to be. The corresponding bit of the number is 1 and the remaining bits are zero. Perform an AND operation on this number and x to get the specified bit in x.

(2) Bitwise OR |

As long as one of them is 1, the result will be 1.

0|0=0; 0|1=1; 1|0=1; 1|1=1;

For example: 51|5 which is 0011 0011 | 0000 0101 =0011 0111 Therefore 51|5=55

Special usage

is often used to set 1 to

certain positions of a data.

Method: Find a number corresponding to the bit of x to be set to 1. The corresponding bit of the number is 1 and the remaining bits are zero. This number is relative to x or sets some position in x to 1.

(3) Exclusive OR ^

If the two corresponding bits are "exclusive" (different values), then the result of the bit is 1, otherwise it is 0

0^0=0; 0^1=1; 1^0=1; 1^1=0;

For example: 51^5 is 0011 0011 ^ 0000 0101 =0011 0110 therefore 51^ 5=54

Special usage

(1)

XOR with 1, makes the specific bit flip

Method: Find a number that corresponds to the bit of

For example: X=1010 1110, flip the lower four bits of

(2)

XOR with 0, keep the original value

For example: X^0000 0000 =1010 1110

(3)

Exchange values ​​between two variables

1. Use the third variable to achieve

C=A;A=B;B=C;

2. Use addition and subtraction to realize the exchange of two variables

A=A+B;B=A-B;A=A-B;

3. Use bitwise XOR operation to achieve it, which is also the most efficient

Principle: The exclusive OR of a number is equal to 0; the exclusive ORoperatorcommutative law

A=A^B;B=A ^B;A=A^B

(4) Negation and operation~

Invert a binary number bitwise, that is, change 0 into 1 and 1 into 0

~1=0;~0=1

(5) Left shift<<

Shift all binary bits of an operand to the left by a certain number of bits (The binary bits on the left are discarded and 0 is added on the right)

For example: 2<<1 =4 10<<1=100

If the high bit discarded when shifting left is not Contains 1, then each left shift is equivalent to multiplying the number by 2.

For example:

11(1011)<<2= 0010 1100=22

11(00000000 00000000 00000000 1011) shaping 32bit

(6) Right shift > . If the high-order bit is not 1 (that is, it is not a negative number) when shifting right, each time the operand is shifted to the right, it is equivalent to dividing the number by 2.

Left padding with 0 or padding with 1 depends on whether the number being moved is positive or negative.

For example: 4>>2=4/2/2=1 -14 (i.e. 1111 0010)>>2 =1111 1100=-4

(7) Unsigned right shift operation>>>

Shift each bit to the right by the specified number of digits,

After the right shift, the vacated bits on the left are filled with zeros

, removed bits on the right are discarded.

For example: -14>>>2 (i.e. 11111111 11111111 11111111 111100

10

)>>>2

= (00111111 11111111 11111111 11111100)=1073741820

##>>>>>>>>>>>> ;>>>>>>>>>>>>>>>>>>>>>>>>> ;>>>>>>>>>>>>>>>>>

mentioned above The binary bit representation of a negative number is slightly different from that of a positive number, so the bitwise operation is also different from that of a positive number. Negative numbers are expressed in their complement form of positive numbers

!

Take the above-mentioned -14 as an example to briefly explain the original code, inverse code and complement code.

Original code

The binary number converted from an integer according to its absolute value is called the original codeFor example: 00000000 00000000 00000000 00001110 is the original code of 14.

Inverse code

Invert the binary number bit by bit, and the resulting new binary number is called the inverse of the original binary number code.

For example: Invert each bit of 00000000 00000000 00000000 0000

1110,

to get 11111111 11111111 11111111 1111

0001

Note: These two are each other’s complement code

complement code

The complement plus 1 is called the complement code 11111111 11111111 11111111 11110001

+1=

##11111111 11111111 11111111 1111

0010

Now we get the binary representation of -14, now shift it left by

-14 (11111111 11111111 11111111 11110010)<<2 =

11111111 11111111 11111111 110010

00

=?

Analysis: The first bit of this binary number is 1, which means it is in two's complement form. Now we need to convert the two's complement code into the original code (its positive value) and convert the original code into one's complement code On the contrary, the steps to convert the complement code to the original code:

The complement code is subtracted by 1 to get the complement code: (11000111) The first 24 bits are 1, and

is omitted here

Reverse the code to get the original code (that is, the positive value of the negative number) (00111000)
Calculate the positive value, the positive value is 56
Take the opposite of the positive value and get the result -56
Conclusion: -14<<2 = -56

4. 三, Base operations in Java

Is binary used a lot in Java?

In normal development, "base conversion" and "bit operations" are not used much, and Java handles high-level tasks.

---

It is often used in cross-platform, such as: file reading and writing, data communication.

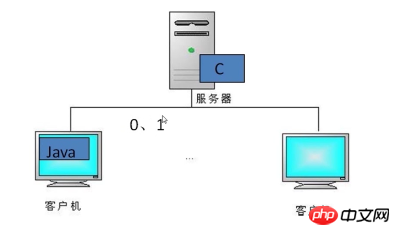
Let’s look at a scenario:

If the client and server are both programs written in Java language, then when the client sends object data, we The data to be sent can be serialized into serializable. After the server gets the serialized data, it can deserialize it and read out the object data inside.

As the number of client visits increases, we do not consider the performance of the server. In fact, a feasible solution is to change the server's Java language to C language.

As the underlying language, C language has a faster response speed than Java language. If the client passes serialized data at this time, the C language on the server side will not be able to parse it. What should I do? We can convert the data to binary (0,1) so that the server can parse these languages.

##>>>>>>>>>>>>>>> ;>>>>>>>>>>>>>>>>>>>>>>>>> ;>>>>>>>>>>>>>>

Basic

data types in JavaThere are the following four types:

1. Int data type: byte (8bit, -128~127), short (16bit), int (32bit), long (64bit)

2. float data type: single precision (float, 32bit), double precision (double, 64bit)

3. The values ​​of boolean type variables are true and false (Both are 1bit)

4. char data type: unicode character, 16bit

Corresponding class type:

Integer, Float, Boolean, Character, Double, Short, Byte, Long ;>>>>>>>>>>>>>>>>>>>>>>>>> ;>>>>>>>>>>>>>>>>

(1) Data type Convert to bytesFor example: int type 8143 (00000000 00000000 00011111 11001111)

=>byte[] b=[-49,31,0,0]

First (low end) byte: 8143>>0*8 & 0xff=(11001111)=207 (or signed -49)

Second (low end) byte: 8143> ;>1*8 &0xff=(00011111)=31

The third (low-end) byte: 8143>>2*8 &0xff=00000000=0

The fourth (Low-end) Bytes: 8143>>3*8 &0xff=00000000=0

We noticed that the above (low-end) starts from right to left, so what? Is it low-end? Let's explain it from the perspective of big and small endian.

Little-Endian method

The low bit bytes are arranged at the low

address end of the memory. The starting address of this value, the

high byte is ranked at the highaddress end of the memoryBig-Endian method(Big-Endian)

The high byte is arranged at the low

address end of the memory, which is the starting address of the value,

The low byte is arranged At the high address end of the memory Why are there big and small endian modes?

This is because in computer systems, we use bytes as units. Each address unit corresponds to a byte, and a byte is 8 bits. However, in

C language

, in addition to 8-bit char, there are also 16-bit short type and 32-bit long type (depending on the specific compiler). In addition, for digits greater than 8 Bit processors, such as 16-bit or 32-bit processors, because the register width is larger than one byte, there must be a problem of arranging multiple bytes. This leads to big-endian storage mode and little-endian storage mode. For example, a 16-bit short type x, the address in the memory is 0x0010, and the value of x is 0x1122, then 0x11 is the high byte and 0x22 is the low byte. For big-endian mode, put 0x11 in the low address, that is, 0x0010, and 0x22 in the high address, that is, 0x0011. Little endian mode is just the opposite. Our commonly used X86 structure is little endian mode, while KEIL C51 is big endian mode. Many ARM and DSP are in little-endian mode. Some ARM processors can also select big-endian or little-endian mode by hardware.

For example: 32-bit number 0x12 34 56 78 (hexadecimal) The storage method of the CPU in Big-Endian mode (assuming it starts from address 0x4000) is

Memory address

0x4000	0x4001	0x4002	0x4003
存放内容	0x78	0x56	0x34	0x12

在Little-Endian模式CPU的存放方式（假设从地址0x4000开始存放）为

内存地址	0x4000	0x4001	0x4002	0x4003
存放内容	0x12	0x34	0x56	0x78

 （二）字符串转化为字节

1.字符串->字节数组

1 String s;2 byte[] bs=s.getBytes();

2.字节数组->字符串

1 Byte[] bs=new byte[int];2 String s =new String(bs);或3 String s=new String(bs,encode);//encode指编码方式，如utf-8

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

两种类型转化为字节的方法都介绍了，下面写个小例子检验一下：

 1 public class BtyeTest { 2     /* 3      * int整型转为byte字节 4      */ 5     public static byte[] intTOBtyes(int in){ 6         byte[] arr=new byte[4]; 7         for(int i=0;i<4;i++){ 8             arr[i]=(byte)((in>>8*i) & 0xff); 9         }10         return arr;11     }12     /*13      * byte字节转为int整型14      */15     public static int bytesToInt(byte[] arr){16         int sum=0;17         for(int i=0;i<arr.length;i++){18             sum+=(int)(arr[i]&0xff)<<8*i;19         }20         return sum;21     }22     public static void main(String[] args) {23         // TODO Auto-generated method stub24         byte[] arr=intTOBtyes(8143);25         for(byte b:arr){26             System.out.print(b+" ");27         }28         System.out.println();29         System.out.println(bytesToInt(arr));30         31         //字符串与字节数组32         String str="云开的立夏de博客园";33         byte[] barr=str.getBytes();34         35         String str2=new String(barr);36         System.out.println("字符串转为字节数组：");37         for(byte b:barr){38             System.out.print(b+" ");39 40         }41         System.out.println();42 43         System.out.println("字节数组换位字符串："+str2);44         45          46     }47 48 }

运行结果：

---

结束语：最近偷懒了，没有好好学习，好几天没写文了，哎，还请大家多多监督！

The above is the detailed content of Detailed explanation of binary and bit operations in Java. For more information, please follow other related articles on the PHP Chinese website!