Python implements the Tower of Hanoi recursive algorithm

When I was learning recursion, there was an exercise called the Tower of Hanoi. The Tower of Hanoi should be a classic introductory case for learning computer recursive algorithms, so I thought I could write a blog to express my opinions. I don’t know how to use this markdown editor yet, maybe the writing format is a bit ugly, please forgive me.

I found a picture of the Tower of Hanoi on the Internet, and the Tower of Hanoi is used Use the middle pillar to stack the disks on the leftmost pillar from large to small. To put it bluntly, c should be the same as the original a

Stop talking nonsense, let’s show the code first

def move(n, a, buffer, c):
  if(n == 1):
    print(a,"->",c)
    return
  move(n-1, a, c, buffer)
  move(1, a, buffer, c)
  move(n-1, buffer, a, c)
move(3, "a", "b", "c")

First, a moving function is defined. The four parameters represent the number of plates on the a-column. , buffer is column b, named buffer for easy understanding. As the name suggests, it is a buffer that moves a to c. Then c is the target column
Let’s read the function code
The general way of writing recursion is that there must be a stop The condition of the recursive loop, so when it is judged that the number of plates on column a is 1, the recursion can be stopped and returned. When there is only one plate on column a, a must be moved to c. The key point is the following code, recursion actually It is a very abstract algorithm. We need to use abstract thinking to think about the Tower of Hanoi problem. Think of the plate on the A column as two, that is, the upper plate and the bottom plate. If it is shown

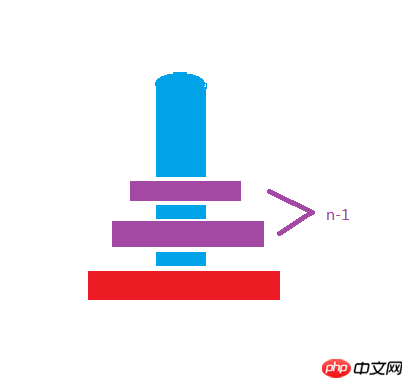
We don’t care how many plates there are on top. Our operation every time is to move the bottom plate to column c through the buffer b-column buffer.
Children’s shoes must be thinking why Jiangzi moves. In fact, this is a summary. If you play the Tower of Hanoi game yourself, you will find the rules. In fact, this game is to constantly think of all the ways above. Move the ones on b to b, then move the last and largest one on a to c, and then rack your brains to move the ones on b to c. At this time, you will find that it turns out that the ones on b also need to pass through the empty one first, which is a. To store the n-1 items above the current b, and then move the largest and last one of b to c. The rules are reflected here. The moving method can also be abstracted, and the program algorithm can be designed based on this.

Let’s use the abstract thinking just now to interpret the remaining code

move(n-1, a, c, buffer)

This code is It means that the n-1 items above the a-column just mentioned are first moved to the buffer through c according to the rules from small to large. This function goes into recursion.

move(1, a, buffer, c)

When the above statement is executed, that is, after the recursive movement of n-1 plates is completed, execute this The statement is to move a plate on column a to c, which is the so-called bottom plate

move(n-1, buffer, a, c)

The last step is to move all the n-1 items on a to the buffer. It must be moved from a to c to complete the movement of the entire Tower of Hanoi. So the last step is naturally to move the n-1 items just now. When the buffer moves to column c through a.
Let me write down the entire moving process, taking 3 on column a as an example

/**
我把3个盘子的汉诺塔全部通过代码演示，按缩进原则，每一个缩进即进一个递归函数，每打印一次即中止当前递归,也就是每个print
说明:
  1.n = 3, n = 2, n = 1是每次执行if(n == 1)的结果，这里就不写判断了，相信童鞋们也能看懂，也就是n不等与1时就减1进入递归
  2.请注意a,b,c柱每次进入函数的顺序，不要被形参带错路了，看准每次函数参数的实参 
**/
move(3, "a", "b", "c")
n=3:
  //开始从a上移动n-1即2个盘子通过c移动到b,以腾出c供a最后一个盘子移动
  move(2, "a","c","b")
  n=2:
  //开始进行n=2的一个递归，把当前a('a')柱上的n-1个盘子通过c('b'）移动到b('c')
    move(1, "a", "b", "c")
    n=1:
    //n=2的第一个递归完成,打印结果，执行当前子函数剩余代码
      print("a", "->", "c") 
    move(1, "a", "c", "b")
    n=1:
      print("a", "->", "b")
    move(1, "c", "a", "b")
    n=1:
      print("c", "->", "b")
  　  //到这里完成了a柱上面的n-1即是2个盘子的移动
//开始把a柱上最后一个盘子移动到c柱上
move(1, "a", "b", "c")
n=1:
  print("a", "->", "c")
  //到这里完成移动a柱上的最后一个盘子到c柱上 
move(2, "b", "a", "c")
n=2:
//开始进行n=2的第二个递归,即把当前b('b')的盘子(n-1个)通过a('a')移动到c('c')上
  move(1, "b", "c", "a")
  n=1:
  //n=2 的第二个递归完成，打印结果并执行当前子函数的剩余代码
    print("b", "->", "a")
  move(1, "b", "a", "c")
  n=1:
    print("b", "->", "c")
  move(1, "a", "b", "c")
  n=1:
    print("a", "->", "c")
    //到这里把b上的盘子通过a移动到c,
//整个代码执行完毕,汉诺塔移动完成

The final print result is:

After children understand the recursive algorithm principle of the Tower of Hanoi, you can write a program to try it. Here is just I learned recursion in Python so I used Python. Children can implement it in other languages. The Tower of Hanoi can really help understand the principle of recursion. The importance of recursion in programming is self-evident!

For more articles related to Python's implementation of the Tower of Hanoi recursive algorithm, please pay attention to the PHP Chinese website!