thinkphp infinite classification implementation method

This article explains the method of implementing infinite classification under the thinkphp framework. Infinite classification is generally used in the classification menu of websites. It is a very common data structure and function. It is also very easy to implement this method in thinkphp. Okay, let's learn how to use it next.

The principle of infinite classification is to add a field (such as Sid) for differentiation. The top-level classification Sid is 0, the second-level classification Sid is the ID of the upper-level classification, and so on. When outputting, recursion is generally used.

Let’s first create a new data table with the following structure:

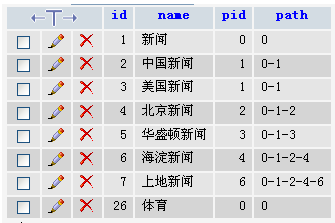
Controller: CateAction .class.php

field("id,name,pid,path,concat(path,'-',id) as bpath")->order('bpath')->select();
 foreach($list as $key=>$value){
 $list[$key]['count']=count(explode('-',$value['bpath']));
 }
 $this->assign('alist',$list);
 $this->display();
 }//添加栏目
 function add(){
 $cate=new CateModel();if($vo=$cate->create()){
 if($cate->add()){
 $this->success('添加栏目成功');
 }else{
 $this->error('添加栏目失败');
 }
 }else{
 $this->error($cate->getError());
 }
 }}
 ?>

Model: CateModel.class.php

where("id=$pid")->find();
 $data=$list['path'].'-'.$list['id'];//子类的path为父类的path加上父类的id
 }
 return $data;
 }
 }
 ?>

Template ：index.html

 请选择父级栏目：
 根栏目
 
 
   {:str_repeat("　",$vo['count']-2)}
 {$vo['name']}
 
 
 

 新的栏目名称：

 
 

The display results are as follows:

---

##Note:

The infinite-level classification implemented in this article uses the ThinkPhP framework. That is to say, the MVC architecture is adopted, in which the controller, template and model layers are clearly written. It is easy to understand for those who can use TP. If there are students who do not understand the TP framework, you can first understand how to use the framework. Looking back at our writing style.