 Java
Java javaTutorial
javaTutorial Graphical explanation of how to implement quickSort quick sorting algorithm in Java
Graphical explanation of how to implement quickSort quick sorting algorithm in JavaGraphical explanation of how to implement quickSort quick sorting algorithm in Java
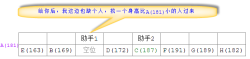
Compared with algorithms such as bubble sorting and selection sorting, the specific algorithm principle and implementation of quick sorting are somewhat difficult. In order to better understand quick sort, we still describe the algorithm principle of quick sort in detail in the form of examples. In the previous sorting algorithm, we took the height sorting problem of 5 athletes as an example to explain. In order to better reflect the characteristics of quick sorting, here we add 3 additional athletes. The details of the eight athletes in the example and their height information are as follows (F, G, and H are new athletes): A(181), B(169), C(187), D(172), E(163), F(191), G(189), H(182)
In the previous sorting algorithm, these sortings were all completed by the coach. Now that the number of athletes has increased, the coach also wants to take the opportunity to take a rest. , so the coach called two assistants and asked them to sort the heights of the eight athletes from left to right and from low to high using the quick sort method.
According to the algorithm principle of quick sorting method, two assistants stand on both sides of the athlete arrangement, as shown in the figure below

First, Assistant 1 starts from Select an athlete from the arrangement (usually the first athlete on the left or the middlemost athlete), here select athlete A (181). Since the sorting is from left to right and from low to high, Assistant 1 needs an athlete whose height is smaller than A(181) (the selected A(181)) as the benchmark for comparison. All comparisons in this round are with Initially selected athlete A (181) comparison):

# Let’s continue to refer to the detailed diagram of the first round of quick sorting.



/**
* 对指定的数组中索引从start到end之间的元素进行快速排序
*
* @param array 指定的数组
* @param start 需要快速排序的数组索引起点
* @param end 需要快速排序的数组索引终点
*/
public static final void quickSort(int[] array, int start, int end) {
// i相当于助手1的位置,j相当于助手2的位置
int i = start, j = end;
int pivot = array[i]; // 取第1个元素为基准元素
int emptyIndex = i; // 表示空位的位置索引,默认为被取出的基准元素的位置
// 如果需要排序的元素个数不止1个,就进入快速排序(只要i和j不同,就表明至少有2个数组元素需要排序)
while (i < j) {
// 助手2开始从右向左一个个地查找小于基准元素的元素
while (i < j && pivot <= array[j])
j--;
if (i < j) {
// 如果助手2在遇到助手1之前就找到了对应的元素,就将该元素给助手1的"空位",j成了空位
array[emptyIndex] = array[emptyIndex = j];
}
// 助手1开始从左向右一个个地查找大于基准元素的元素
while (i < j && array[i] <= pivot)
i++;
if (i < j) {
// 如果助手1在遇到助手2之前就找到了对应的元素,就将该元素给助手2的"空位",i成了空位
array[emptyIndex] = array[emptyIndex = i];
}
}
// 助手1和助手2相遇后会停止循环,将最初取出的基准值给最后的空位
array[emptyIndex] = pivot;
// =====本轮快速排序完成=====
// 如果分割点i左侧有2个以上的元素,递归调用继续对其进行快速排序
if (i - start > 1) {
quickSort(array, 0, i - 1);
}
// 如果分割点j右侧有2个以上的元素,递归调用继续对其进行快速排序
if (end - j > 1) {
quickSort(array, j + 1, end);
}
}
//主方法
public static void main(String[] args) {
// =====使用快速排序法对表示8名运动员身高的数组heights进行从低到高的排序=====
// A(181)、B(169)、C(187)、D(172)、E(163)、F(191)、G(189)、H(182)
int[] heights = { 181, 169, 187, 172, 163, 191, 189, 182 };
// 调用快速排序方法
quickSort(heights, 0, heights.length - 1);
// 输出排序后的结果
for (int height : heights) {
System.out.println(height);
}
} The output of the above Java code is as follows: 163 169 172 181 182 187 189 191Note: Due to local differences in thinking, the code implementation of the above quick sort may have multiple variations. However, no matter what form of variation, the core idea of quick sort does not change. Another implementation: one-way scanning
There is another version of one-way scanning for quick sorting array splitting. The specific steps are to select the last element in the array as the splitting element, and set the same Two pointers, pointer i points to the position before the first element in the array, and pointer j points to the first element in the array. j scans from front to right, left to right, and increases i by one when it encounters an element that is less than or equal to the split element, and then swaps the elements pointed to by i and j. Finally, swap the element at position i+1 with the split element to complete an array division. The code is implemented as follows:
int partition(int[] a, int lo, int hi) {
int i = lo - 1, j = lo;
int v = a[hi];
while (j < hi) {
if (a[j] <= v) {
swap(a, ++i, j);
}
j++;
}
swap(a, i + 1, hi);
return i + 1;
}For more pictures and texts explaining the method of implementing the quickSort quick sorting algorithm in Java, please pay attention to the PHP Chinese website for related articles!
 How does platform independence benefit enterprise-level Java applications?May 03, 2025 am 12:23 AM
How does platform independence benefit enterprise-level Java applications?May 03, 2025 am 12:23 AMJava is widely used in enterprise-level applications because of its platform independence. 1) Platform independence is implemented through Java virtual machine (JVM), so that the code can run on any platform that supports Java. 2) It simplifies cross-platform deployment and development processes, providing greater flexibility and scalability. 3) However, it is necessary to pay attention to performance differences and third-party library compatibility and adopt best practices such as using pure Java code and cross-platform testing.
 What role does Java play in the development of IoT (Internet of Things) devices, considering platform independence?May 03, 2025 am 12:22 AM
What role does Java play in the development of IoT (Internet of Things) devices, considering platform independence?May 03, 2025 am 12:22 AMJavaplaysasignificantroleinIoTduetoitsplatformindependence.1)Itallowscodetobewrittenonceandrunonvariousdevices.2)Java'secosystemprovidesusefullibrariesforIoT.3)ItssecurityfeaturesenhanceIoTsystemsafety.However,developersmustaddressmemoryandstartuptim
 Describe a scenario where you encountered a platform-specific issue in Java and how you resolved it.May 03, 2025 am 12:21 AM
Describe a scenario where you encountered a platform-specific issue in Java and how you resolved it.May 03, 2025 am 12:21 AMThesolutiontohandlefilepathsacrossWindowsandLinuxinJavaistousePaths.get()fromthejava.nio.filepackage.1)UsePaths.get()withSystem.getProperty("user.dir")andtherelativepathtoconstructthefilepath.2)ConverttheresultingPathobjecttoaFileobjectifne
 What are the benefits of Java's platform independence for developers?May 03, 2025 am 12:15 AM
What are the benefits of Java's platform independence for developers?May 03, 2025 am 12:15 AMJava'splatformindependenceissignificantbecauseitallowsdeveloperstowritecodeonceandrunitonanyplatformwithaJVM.This"writeonce,runanywhere"(WORA)approachoffers:1)Cross-platformcompatibility,enablingdeploymentacrossdifferentOSwithoutissues;2)Re
 What are the advantages of using Java for web applications that need to run on different servers?May 03, 2025 am 12:13 AM
What are the advantages of using Java for web applications that need to run on different servers?May 03, 2025 am 12:13 AMJava is suitable for developing cross-server web applications. 1) Java's "write once, run everywhere" philosophy makes its code run on any platform that supports JVM. 2) Java has a rich ecosystem, including tools such as Spring and Hibernate, to simplify the development process. 3) Java performs excellently in performance and security, providing efficient memory management and strong security guarantees.
 How does the JVM contribute to Java's 'write once, run anywhere' (WORA) capability?May 02, 2025 am 12:25 AM
How does the JVM contribute to Java's 'write once, run anywhere' (WORA) capability?May 02, 2025 am 12:25 AMJVM implements the WORA features of Java through bytecode interpretation, platform-independent APIs and dynamic class loading: 1. Bytecode is interpreted as machine code to ensure cross-platform operation; 2. Standard API abstract operating system differences; 3. Classes are loaded dynamically at runtime to ensure consistency.
 How do newer versions of Java address platform-specific issues?May 02, 2025 am 12:18 AM
How do newer versions of Java address platform-specific issues?May 02, 2025 am 12:18 AMThe latest version of Java effectively solves platform-specific problems through JVM optimization, standard library improvements and third-party library support. 1) JVM optimization, such as Java11's ZGC improves garbage collection performance. 2) Standard library improvements, such as Java9's module system reducing platform-related problems. 3) Third-party libraries provide platform-optimized versions, such as OpenCV.
 Explain the process of bytecode verification performed by the JVM.May 02, 2025 am 12:18 AM
Explain the process of bytecode verification performed by the JVM.May 02, 2025 am 12:18 AMThe JVM's bytecode verification process includes four key steps: 1) Check whether the class file format complies with the specifications, 2) Verify the validity and correctness of the bytecode instructions, 3) Perform data flow analysis to ensure type safety, and 4) Balancing the thoroughness and performance of verification. Through these steps, the JVM ensures that only secure, correct bytecode is executed, thereby protecting the integrity and security of the program.


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

Dreamweaver CS6
Visual web development tools





