 Backend Development
Backend Development PHP Tutorial
PHP Tutorial A painful interview question, painful interview question_PHP tutorial
A painful interview question, painful interview question_PHP tutorialA painful interview question, a painful interview question
Yesterday I saw two interview questions, there were two, and many people answered the first one. Few people answered the second question. I am learning PHP recently, so this article uses PHP as the basis to bring the second analysis today.
Attached are two interview questions:
1: There are 100 lights in the hall, and each light is numbered, ranging from 1-100. Each light is controlled by a switch. (Press the switch once to turn the light on, and press it again to turn off the light. The number of the switch is the same as the controlled light.) At the beginning, all the lights are off. Now press the switch according to the following rules.
For the first time, light all the lights.
For the second time, press all switches that are multiples of 2.
For the third time, press all switches that are multiples of 3.
And so on. For the Nth time, press all switches that are multiples of N.
Ask how many lights are still on in the hall after pressing the button for the 100th time.
2: There is a 27 cm thin wooden pole, and there is an ant at each of the five positions: 3 cm, 7 cm, 11 cm, 17 cm, and 23 cm. The wooden pole is very thin and cannot pass an ant at the same time. At the beginning, it was arbitrary whether the ants' heads were facing left or right. They would only walk forward or turn around, but not retreat. When any two ants meet, they will turn around and walk in opposite directions at the same time. Suppose ants can move one centimeter per second. Write a program to find the minimum time and maximum time for all ants to leave the wooden pole.
The first one is relatively simple and I won’t go into details about it, but the second one makes people have a headache just by looking at it.
Let’s briefly analyze this question.
Judging from the question itself, it seems that considering the positions of five ants at the same time is really confusing. Fortunately, the last sentence of the question is still very useful. The maximum time and minimum time for all ants to leave the wooden pole. Use the thin rod as a horizontal axis. The positions of the ants have been given. When the position of the last ant leaving is =27, all ants leave the wooden pole. (This seems to be nonsense.)
1 meter per second, this question setting is comfortable enough. After all, the time the ant moves here is numerically equal to the value of the distance the ant moves. (If it is considered that all ants leave the wooden pole and continue to move at the original speed). And they are simultaneously moving.
There are only two directions of movement of ants, left or right. Considering the actual situation of the coordinate axes, if we assume that moving to the right is 1, then the equivalent movement to the left is -1. It is important to consider this step in the binary world of computers.
Okay, the front is the foreshadowing. Whether you understand it or not, here is the more important content .
Finding the maximum time and minimum time is just like finding the maximum and minimum numbers in a pile of numbers. This kind of thing should not be difficult. The key is to find the last time to do the comparison. What does time have to do with anything? Judging from the title design, it should only be related to the initial motion status of each ant. As for the movement status of a certain ant at a certain moment during the period, do we need to worry about it? No need. That would only complicate the problem.
How many initial states are there for ants? 2^5=32. Obviously each of these 32 types of time needs to be calculated, and a simple loop can be used.
Focusing on the movement status of ants is nothing more than two variables: position and direction. So here I simply introduce two arrays $arr and $b . The former is used to describe the current position of a certain point, and the latter is used to describe the current direction. $b[i]
As described previously, the value should only be -1 or 1.
Considering this, we can straighten our thinking and assign an initial value to the arrays '$arr' and '$b'. Use time '$i' to make a loop. After each ant moves every second, when '$arr[$k]==$arr[$k-1]', change the matching state value '$b[k ]' value. When the 'value' of all '$arr' is =27, stop looping and return '$i'. A lot of loop traversal is used. Of course, for simplicity, when '$arr[$k]' is no longer on the pole, you can use the unset() function to delete it. Finally, it is judged that '$arr' is empty to end the loop.
After talking about the main content, we still have to deal with a small detail, How to generate the array "$b" that describes the movement status of ants?
You can’t generate it manually. There are 32 situations for 5 ants, and 1024 situations for 10 ants. It’s really painful to generate them manually. But you obviously know to generate 32 arrays, so you have to use it. Therefore, it is easy for us to think of converting a decimal number into a binary number of length 5. Then replace the 0 in this binary number with -1. Convert the replaced string into an array.
Paste the corresponding code:
<?<span>php
</span><span>for</span>(<span>$j</span>=0;<span>$j</span><32;<span>$j</span>++<span>){
</span><span>$var</span>=<span>sprintf</span>("%05b", <span>$j</span><span>);
</span><span>$var</span>=<span>str_replace</span>('1', '1|', <span>$var</span><span>);
</span><span>$var</span>=<span>str_replace</span>('0', '-1|', <span>$var</span><span>);
</span><span>$b</span>=<span>explode</span>('|',<span>$var</span><span>);
</span><span>$res</span>=getRes(<span>$b</span><span>);
</span><span>if</span> (<span>isset</span>(<span>$min</span><span>)) {
</span><span>if</span> (<span>$res</span><<span>$min</span><span>) {
</span><span>$min</span>=<span>$res</span><span>;
}
}</span><span>else</span><span>{
</span><span>$min</span>=<span>$res</span><span>;
}
</span><span>if</span> (<span>isset</span>(<span>$max</span><span>)) {
</span><span>if</span> (<span>$res</span>><span>$max</span><span>) {
</span><span>$max</span>=<span>$res</span><span>;
}
}</span><span>else</span><span>{
</span><span>$max</span>=<span>$res</span><span>;
}
</span><span>print_r</span>(<span>$b</span><span>);
</span><span>echo</span> "此次结果是".<span>$res</span>.' $max='.<span>$max</span>.' $min='.<span>$min</span><span>;
</span><span>echo</span> "<hr/>"<span>;
}
</span><span>echo</span> "最大值是".<span>$max</span>."最小值是".<span>$min</span><span>;
</span><span>//</span><span>获得某种情况下的时间</span>
<span>function</span> getRes(<span>$b</span><span>){
</span><span>$arr</span>=<span>array</span>(3,7,11,17,23<span>);
</span><span>for</span>(<span>$i</span>=1;<span>$i</span><100;<span>$i</span>++<span>){
</span><span>foreach</span> (<span>$arr</span> <span>as</span> <span>$k</span> => <span>$val</span><span>) {
</span><span>$arr</span>[<span>$k</span>]=<span>$val</span>+<span>$b</span>[<span>$k</span><span>];
</span><span>if</span> (<span>$arr</span>[<span>$k</span>]==@<span>$arr</span>[<span>$k</span>-1<span>]) {
</span><span>$b</span>[<span>$k</span>]=-<span>$b</span>[<span>$k</span><span>];
</span><span>$b</span>[<span>$k</span>-1]=-@<span>$b</span>[<span>$k</span>-1<span>];
}
</span><span>if</span> ((<span>$arr</span>[<span>$k</span>]>=27)||(<span>$arr</span>[<span>$k</span>]<=0<span>)) {
</span><span>unset</span>(<span>$arr</span>[<span>$k</span><span>]);
}
}
</span><span>if</span> (<span>empty</span>(<span>$arr</span><span>)) {
</span><span>return</span> <span>$i</span><span>;
}
}
}</span>
This is a routine, follow the rules and go through it step by step, but it is indeed very hard.
---------------------------------------- ---gorgeous divider--- -------------------------------------------------- ----------------------------------
在我一本正经地胡说八道后,就没有更加好的想法?
那就是相遇的时候,两只蚂蚁开始掉头。如果不掉头直接走呢?和他们掉头后有什么差别?结果是没有差别!每只蚂蚁开头拿一个接力棒,碰头后,两人交换接力棒,虽然蚂蚁掉头了,但接力棒可是一直往初始方向走哦~所以解题前景变得无比明朗。知道某只蚂蚁的初始状态,就知道他开始拿的接力棒最后走了多久!至于接力棒是不是亲生的,那你管哩。反正最后一个接力棒离开杆子,最后一只蚂蚁也离开杆子。
因而获得某种初始状态下的时间还可以这样写:
<span>function</span> getRes(<span>$b</span><span>){
</span><span>$arr</span>=<span>array</span>(3,7,11,17,23<span>);
</span><span>for</span>(<span>$i</span>=1;;<span>$i</span>++<span>){
</span><span>foreach</span> (<span>$arr</span> <span>as</span> <span>$k</span> => <span>$val</span><span>) {
</span><span>$arr</span>[<span>$k</span>]=<span>$val</span>+<span>$b</span>[<span>$k</span><span>];
</span><span>if</span> ((<span>$arr</span>[<span>$k</span>]>=27)||(<span>$arr</span>[<span>$k</span>]<=0<span>)) {
</span><span>unset</span>(<span>$arr</span>[<span>$k</span><span>]);
}
}
</span><span>if</span> (<span>empty</span>(<span>$arr</span><span>)) {
</span><span>return</span> <span>$i</span><span>;
}
}
}</span>
------------------------------------- ---华丽的分隔线-------------------------------------------------------------------------------------------
当然问题可以更加简化,连上面的代码都用不到了。
通过上面分析可以看做每只蚂蚁直接走互不影响。到最后求最大值最小值的时候实际上可以先算出每只蚂蚁到两端的距离。形成五组数字。(3,24),(7,20),(11,16),(10,17),(4,23)在五组数每组数中较小值形成的5个数中最大的一个是最后结果的最小值。 五组数每组数中较大的5个数中最大的那个是结果的最大值。很容易看出来是11和24。为什么呢?典型的木桶效应啊。最后一只蚂蚁走出去了才能算完成整个事情。五只蚂蚁全部最短路径出去,得到结果才可能是最快的,五只蚂蚁全部最长路径出去,耗时才能是最慢的。
ps:应该不会有更快的想法了吧。
最后感谢@randeng在本问题上的指点~
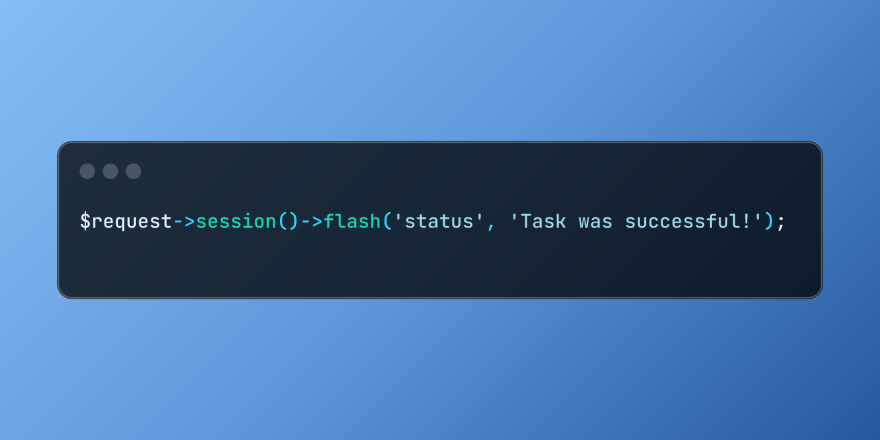 Working with Flash Session Data in LaravelMar 12, 2025 pm 05:08 PM
Working with Flash Session Data in LaravelMar 12, 2025 pm 05:08 PMLaravel simplifies handling temporary session data using its intuitive flash methods. This is perfect for displaying brief messages, alerts, or notifications within your application. Data persists only for the subsequent request by default: $request-
 Build a React App With a Laravel Back End: Part 2, ReactMar 04, 2025 am 09:33 AM
Build a React App With a Laravel Back End: Part 2, ReactMar 04, 2025 am 09:33 AMThis is the second and final part of the series on building a React application with a Laravel back-end. In the first part of the series, we created a RESTful API using Laravel for a basic product-listing application. In this tutorial, we will be dev
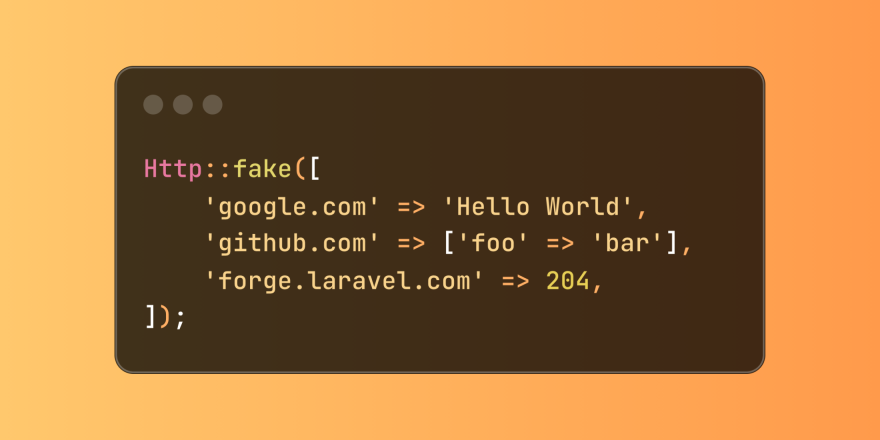 Simplified HTTP Response Mocking in Laravel TestsMar 12, 2025 pm 05:09 PM
Simplified HTTP Response Mocking in Laravel TestsMar 12, 2025 pm 05:09 PMLaravel provides concise HTTP response simulation syntax, simplifying HTTP interaction testing. This approach significantly reduces code redundancy while making your test simulation more intuitive. The basic implementation provides a variety of response type shortcuts: use Illuminate\Support\Facades\Http; Http::fake([ 'google.com' => 'Hello World', 'github.com' => ['foo' => 'bar'], 'forge.laravel.com' =>
 cURL in PHP: How to Use the PHP cURL Extension in REST APIsMar 14, 2025 am 11:42 AM
cURL in PHP: How to Use the PHP cURL Extension in REST APIsMar 14, 2025 am 11:42 AMThe PHP Client URL (cURL) extension is a powerful tool for developers, enabling seamless interaction with remote servers and REST APIs. By leveraging libcurl, a well-respected multi-protocol file transfer library, PHP cURL facilitates efficient execution of various network protocols, including HTTP, HTTPS, and FTP. This extension offers granular control over HTTP requests, supports multiple concurrent operations, and provides built-in security features.
 12 Best PHP Chat Scripts on CodeCanyonMar 13, 2025 pm 12:08 PM
12 Best PHP Chat Scripts on CodeCanyonMar 13, 2025 pm 12:08 PMDo you want to provide real-time, instant solutions to your customers' most pressing problems? Live chat lets you have real-time conversations with customers and resolve their problems instantly. It allows you to provide faster service to your custom
 Notifications in LaravelMar 04, 2025 am 09:22 AM
Notifications in LaravelMar 04, 2025 am 09:22 AMIn this article, we're going to explore the notification system in the Laravel web framework. The notification system in Laravel allows you to send notifications to users over different channels. Today, we'll discuss how you can send notifications ov
 Explain the concept of late static binding in PHP.Mar 21, 2025 pm 01:33 PM
Explain the concept of late static binding in PHP.Mar 21, 2025 pm 01:33 PMArticle discusses late static binding (LSB) in PHP, introduced in PHP 5.3, allowing runtime resolution of static method calls for more flexible inheritance.Main issue: LSB vs. traditional polymorphism; LSB's practical applications and potential perfo
 PHP Logging: Best Practices for PHP Log AnalysisMar 10, 2025 pm 02:32 PM
PHP Logging: Best Practices for PHP Log AnalysisMar 10, 2025 pm 02:32 PMPHP logging is essential for monitoring and debugging web applications, as well as capturing critical events, errors, and runtime behavior. It provides valuable insights into system performance, helps identify issues, and supports faster troubleshoot


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Zend Studio 13.0.1
Powerful PHP integrated development environment

Notepad++7.3.1
Easy-to-use and free code editor

Atom editor mac version download
The most popular open source editor

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.






