jsvascript image processing—(computer vision application) image pyramid_javascript skills

Foreword
In the previous article, we explained the edge gradient calculation function. In this article we will learn about the image pyramid.

Image pyramid?
Image pyramids are widely used in computer vision applications.
Image pyramid is a collection of images. All images in the collection originate from the same original image and are obtained by continuously downsampling the original image.

There are two common image pyramids :
•Gaussian pyramid: used for downsampling
•Laplacian pyramid : Used to reconstruct the upper unsampled image from the lower level image of the pyramid

Gaussian Pyramid

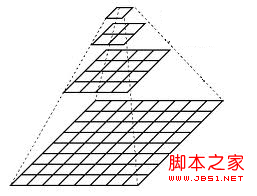
Similar to a pyramid, the Gaussian pyramid gradually downsamples the underlying original image and becomes smaller and smaller.

So how to get the next layer of images?
First, convolve with Gaussian kernel:

Then, delete all even-numbered rows and columns.
It can be seen that the next level image is about 1/4 of the previous level.

So how to transform upward?
First expand the image rows and columns to twice the original size, and then fill the added rows and columns with 0s.
Finally, multiply the Gaussian kernel just by 4 and post-convolution.

Gaussian pyramid implementation

Copy code The code is as follows:

var pyrDown = function(__src, __dst){
__src || error(arguments.callee, IS_UNDEFINED_OR_NULL/* {line} */);
if(__src.type && __src.type == " CV_RGBA"){
var width = __src.col,
height = __src.row,
dWidth = ((width & 1) width) / 2,
dHeight = ((height & 1) height) / 2,
sData = __src.data,
dst = __dst || new Mat(dHeight, dWidth, CV_RGBA),
dstData = dst.data;
var withBorderMat = copyMakeBorder(__src , 2, 2, 0, 0),
mData = withBorderMat.data,
mWidth = withBorderMat.col;
var newValue, nowX, offsetY, offsetI, dOffsetI, i, j;
var kernel = [1, 4, 6, 4, 1,
, 16, 24, 16, 4,
, 24, 36, 24, 6,
, 16, 24, 16, 4,
, 4, 6, 4, 1
];
for(i = dHeight; i--;){
dOffsetI = i * dWidth;
for(j = dWidth; j- -;){
for(c = 3; c--;){
newValue = 0;
for(y = 5; y--;){
offsetY = (y i * 2 ) * mWidth * 4;
for(x = 5; x--;){
nowX = (x j * 2) * 4 c;
newValue = (mData[offsetY nowX] * kernel[y * 5 x]);
}
}
dstData[(j dOffsetI) * 4 c] = newValue / 256;
}
dstData[(j dOffsetI) * 4 3] = mData[offsetY 2 * mWidth * 4 (j * 2 2) * 4 3];
}
}
}else{
error(arguments.callee, UNSPPORT_DATA_TYPE/* {line} */ );
}
return dst;
};

dWidth = ((width & 1) width) / 2,
dHeight = ((height & 1) height) / 2
Here a & 1 is equivalent to a % 2, that is, the remainder after dividing by 2.
We did not follow the above steps when implementing it, because this would be inefficient. Instead, we directly created a matrix that was 1/4 of the original matrix, and then skipped the rows and columns to be deleted during convolution.

The same is true below. After creating the convolution, since some places must be 0, some elements of the kernel are ignored during the actual convolution process.

Copy code The code is as follows:

var pyrUp = function(__src, __dst){
__src || error(arguments.callee, IS_UNDEFINED_OR_NULL/* {line} */);
if(__src.type && __src.type == "CV_RGBA"){
var width = __src.col,
height = __src.row,
dWidth = width * 2,
dHeight = height * 2,
sData = __src.data,
dst = __dst || new Mat(dHeight, dWidth, CV_RGBA),
dstData = dst.data;
var withBorderMat = copyMakeBorder(__src, 2, 2, 0, 0),
mData = withBorderMat.data,
mWidth = withBorderMat.col;
var newValue, nowX, offsetY, offsetI, dOffsetI, i, j;
var kernel = [1, 4, 6, 4, 1,
, 16, 24, 16, 4,
, 24, 36, 24, 6,
, 16, 24, 16, 4,
, 4, 6, 4, 1
];
for(i = dHeight; i--;){
dOffsetI = i * dWidth;
for(j = dWidth; j--;){
for(c = 3; c--;){
newValue = 0;
for(y = 2 (i & 1); y--;){
offsetY = (y ((i 1) >> 1)) * mWidth * 4;
for(x = 2 (j & 1); x--;){
nowX = (x ((j 1) >> 1)) * 4 c;
newValue = (mData[offsetY nowX] * kernel[(y * 2 (i & 1 ^ 1)) * 5 (x * 2 (j & 1 ^ 1))]);
}
}
dstData[(j dOffsetI) * 4 c] = newValue / 64;
}
dstData[(j dOffsetI) * 4 3] = mData[offsetY 2 * mWidth * 4 (((j 1) >> 1) 2) * 4 3];
}
}
}else{
error(arguments.callee, UNSPPORT_DATA_TYPE/* {line} */);
}
return dst;
};

效果图