javascript image processing - deep understanding of affine transformation_javascript skills

Foreword

In the previous article , we explained the image pyramid. In this article we will learn about affine transformation.

Affine?

Any affine transformation can be converted to, multiplied by a matrix (linear change), plus a vector (translational change).

In fact, affine is the transformation relationship between two pictures.

For example, we can perform operations on images through affine transformation: scaling, rotation, translation, etc.

A math problem

Before solving the affine problem, let’s do a math problem.

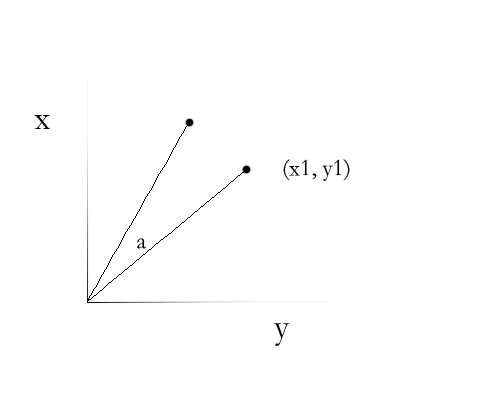
As shown in the figure, for point (x1, y1), it is rotated by an angle a relative to the origin, so where does this point go?

We change the coordinate system into a polar coordinate system, then the point (x1, y1) becomes (r, β), and after rotation it becomes (r, α β) .

Return to the Cartesian coordinate system, then the rotated point becomes (cos(α β) * r, sin(α β) * r).

Then use the formula :

cos（α β）=cosαcosβ-sinαsinβ

sin（α β）=sinαcosβ cosαsinβ

and the original point is (cosβ * r, sinβ * r), so it is easy to get the new point as (x1 * cosα - y1 * sinα, x1 * sinaα y1 *cosα).

We can derive the rotation transformation formula from it:

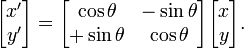
Then translation is relatively simple, it is equivalent to adding a vector (c, d).

Get the transformation matrix function implementation

Usually we use matrix to represent affine transformation.

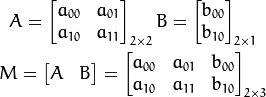
Where A is the rotation scaling transformation, and B is the translation transformation. Then the result T satisfies:

or

That is:

Copy code The code is as follows:

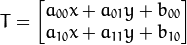
var getRotationArray2D = function (__angle, __x, __y){
var sin = Math.sin(__angle) || 0,
cos = Math.cos(__angle) || 1,
x = __x || 0,
y = __y || 0;

return [cos, -sin, -x,
sin, cos, -y
];
};

In this way we get an affine transformation matrix.

Of course, this implementation itself has certain problems, because the origin is fixed at the upper left corner.

Affine transformation implementation

Copy code The code is as follows:

var warpAffine = function(__src, __rotArray, __dst){
(__src && __rotArray) || error(arguments.callee, IS_UNDEFINED_OR_NULL/* {line} */);
if(__src.type && __src. type === "CV_RGBA"){
var height = __src.row,
width = __src.col,
dst = __dst || new Mat(height, width, CV_RGBA),
sData = new Uint32Array(__src.buffer),
dData = new Uint32Array(dst.buffer);

var i, j, xs, ys, x, y, nowPix;

for (j = 0, nowPix = 0; j xs = __rotArray[1] * j __rotArray[2];
ys = __rotArray[4] * j __rotArray[5];
for(i = 0; i
if(xs > 0 && ys > 0 && xs
y = ys | 0;
x = xs | 0;

dData[nowPix] = sData[y * width x] ;
}else{
dData[nowPix] = 4278190080; //Black
}
}
}
}else{
error(arguments.callee, UNSPPORT_DATA_TYPE/* {line} */);
}
return dst;
};

This function first converts the matrix data into 32-bit form, and operating each element is equivalent to operating each pixel.

Then traverse all elements and assign values ​​to the corresponding points.

Effect